Abstract
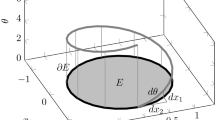
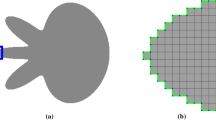
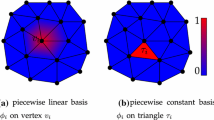
Length and area regularization are commonplace for inverse problems today. It has however turned out to be much more difficult to incorporate a curvature prior. In this paper we propose several improvements to a recently proposed framework based on global optimization. We identify and solve an issue with extraneous arcs in the original formulation by introducing region consistency constraints. The mesh geometry is analyzed both from a theoretical and experimental viewpoint and hexagonal meshes are shown to be superior. We demonstrate that adaptively generated meshes significantly improve the performance. Our final contribution is that we generalize the framework to handle mean curvature regularization for 3D surface completion and segmentation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Woodford, O., Torr, P.H.S., Reid, I., Fitzgibbon, A.W.: Global stereo reconstruction under second order smoothness priors. IEEE Trans. Pattern Analysis and Machine Intelligence 31, 2115–2128 (2009)
El-Zehiry, N., Grady, L.: Fast global optimization of curvature. In: Conf. Computer Vision and Pattern Recognition (2010)
Schoenemann, T., Kahl, F., Cremers, D.: Curvature regularity for region-based image segmentation and inpainting: A linear programming relaxation. In: Int. Conf. Computer Vision (2009)
Kanizsa, G.: Contours without gradients or cognitive contours. Italian Jour. Psych. 1, 93–112 (1971)
Dobbins, A., Zucker, S.W., Cynader, M.S.: Endstopped neurons in the visual cortex as a substrate for calculating curvature. Nature 329, 438–441 (1987)
Willmore, T.J.: Note on embedded surfaces. An. Sti. Univ. ”Al. I. Cuza” Iasi Sect. I a Mat (N.S.), 493–496 (1965)
Hsu, L., Kusner, R., Sullivan, J.: Minimizing the squared mean curvature integral for surfaces in space forms. Experimental Mathematics 1, 191–207 (1992)
Kawai, N., Sato, T., Yokoya, N.: Efficient surface completion using principal curvature and its evaluation. In: Int. Conf. Image Processing, pp. 521–524 (2009)
Masnou, S.: Disocclusion: A variational approach using level lines. IEEE Transactions on Image Processing 11, 68–76 (2002)
Sullivan, J.: Crystalline Approximation Theorem for Hypersurfaces. PhD thesis, Princeton Univ. (1990)
Grady, L.: Minimal surfaces extend shortest path segmentation methods to 3D. IEEE Trans. on Pattern Analysis and Machine Intelligence 32(2), 321–334 (2010)
Bruckstein, A.M., Netravali, A.N., Richardson, T.J.: Epi-convergence of discrete elastica. Applicable Analysis, Bob Caroll Special Issue 79, 137–171 (2001)
Wardetzky, M., Bergou, M., Harmon, D., Zorin, D., Grinspun, E.: Discrete quadratic curvature energies. Comput. Aided Geom. Des. 24(8-9), 499–518 (2007)
Rother, C., Kolmogorov, V., Lempitsky, V., Szummer, M.: Optimizing binary MRFs via extended roof duality. In: Conf. Computer Vision and Pattern Recognition (2007)
Middleton, L., Sivaswamy, J.: Hexagonal Image Processing: A Practical Approach. Springer, New York (2005)
Hales, T.C.: The honeycomb conjecture. Discrete & Computational Geometry 25, 1–22 (2001)
Xu, M., Thompson, P.M., Toga, A.W.: An adaptive level set segmentation on a triangulated mesh. IEEE Trans. on Medical Imaging 23, 191–201 (2004)
Kirsanov, D., Gortler, S.J.: A discrete global minimization algorithm for continuous variational problems. Technical Report TR-14-04, Harvard (2004)
Schoenemann, T., Kuang, Y., Kahl, F.: Curvature regularity for multi-label problems — standard and customized linear programming. In: Boykov, Y., et al. (eds.) EMMCVPR 2011. LNCS, vol. 6819, pp. 205–218. Springer, Heidelberg (2011)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Strandmark, P., Kahl, F. (2011). Curvature Regularization for Curves and Surfaces in a Global Optimization Framework. In: Boykov, Y., Kahl, F., Lempitsky, V., Schmidt, F.R. (eds) Energy Minimization Methods in Computer Vision and Pattern Recognition. EMMCVPR 2011. Lecture Notes in Computer Science, vol 6819. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-23094-3_15
Download citation
DOI: https://doi.org/10.1007/978-3-642-23094-3_15
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-23093-6
Online ISBN: 978-3-642-23094-3
eBook Packages: Computer ScienceComputer Science (R0)