Abstract
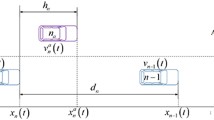
We investigated the effect of the slope upon traffic flow on a single lane highway with an uphill gradient and a downhill gradient. The model was improved by introducing the variable brake distance on different gradient. A simulation is carried out to examine the validity and reasonability of the improved model. The result of the simulation shows that the amplitude of the density waves decreases with the decrease of the slope of the gradient on highway. Moreover the density waves propagate backward. The results indicated that the new model was reasonable and valid in describing the motion of the vehicles on highway with some gradients.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Pipes, L.A.: An operational analysis of traffic dynamics. J. Appl. Phys. 24, 274–281 (1953)
Bando, M., Hasebe, K.: Dynamical model of traffic congestion and numerical simulation. Phys. Rev. E 51, 1035–1042 (1995)
Kerner, B.S., Konhauser, P.: Structure and parameters of clusters in traffic flow. Phys. Rev. E 48, 2335–2367 (1993)
Sawada, S.: Nonlinear analysis of a differential-difference equation with next-nearest-neighbour interaction for traffic flow. J. Phys. A: Math. Gen. 34, 11253–11259 (2001)
Hasebe, K., Nakayama, A., Sugiyama, Y.: Dynamical model of a cooperative driving system for freeway traffic. Phys. Rev. E 68, 26102 (2003)
Komatsu, T., Sasa, S.: Kink soliton characterizing traffic congestion. Phys. Rev. E 52, 5574–5582 (1995)
Nagatani, T.: Stabilization and enhancement of traffic flow by the next-nearest-neighbor interaction. Phys. Rev. E 60, 6395–6401 (1999)
Lighthill, M.J., Whitham, G.B.: On Kinematic Waves. I. Flood Movement in Long Rivers. In: Proc. Roy. Soc. A, vol. 229, pp. 281–316 (1995)
Richards, P.I.: Shock Waves on the Highway. Oper. Res. 4, 42–51 (1960)
Tang, T.Q., Huang, H.J., Xu, X.Y., Xue, Y.: Analysis of density wave in two-lane traffic. Chin. Phys. Letters 24, 1410–1413 (2007)
Hasebe, K., Nakayama, A., Sugiyama, Y.: Dynamical model of a cooperative driving system for freeway traffic. Phys. Rev. E 68, 26–102 (2003)
Hasebe, K., Nakayama, A., Sugiyama, Y.: Equivalence of linear response among extended optimal velocity models. Phys. Rev. E 69, 17103 (2004)
Lenz, H., Wagner, C.K., Sollacher, R.: Multi-anticipative car-following model. Eur. Phys. J. B 7, 331–340 (1998)
Ge, H.X., Dai, S.Q., Dong, L.Y., Xue, Y.: Stabilization effect of traffic flow in an extended car-following model based on an intelligent transportation system application. Phys. Rev. E 70, 66134 (2004)
Jiang, R., Wu, Q.S., Zhu, Z.J.: Full velocity difference model for a car-following theory. Phys. Rev. E 64, 17–101 (2001)
Li, Z.P., Liu, Y.C.: Analysis of stability and density waves of traffic flow model in an ITS environment. Euro. Phys. J. B 53, 367–372 (2006)
Zhu, W.X., Jia, L.: Stability and kink-antikink soliton solutions for total generalized optimal velocity model. International Journal of Modern Physics C 19, 1321–1334 (2008)
Zhu, W.X., Jia, L.: Nonlinear analysis of a synthesized optimal velocity model for traffic flow. Communications in Theoretical Physics 50, 505–509 (2008)
Zhu, W.X., Liu, Y.C.: Total generalized optimal velocity model and its numerical test. Journal of Shanghai Jiaotong University (English Edition) 13, 166–170 (2008)
Yu, L., Li, T., Shi, Z.K.: Density Waves in a traffic flow model with a reaction time delay. Physica A 398, 2607–2616 (2010)
Komada, K., Masakura, S., Nagatani, T.: Effect of gravitational force upon traffic flow with gradients. Physica A 388, 2880–2894 (2009)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Zhu, WX., Jia, ZP. (2011). Improved Car-Following Model for Traffic Flow and Its Numerical Simulation on Highway with Gradients. In: Lin, S., Huang, X. (eds) Advances in Computer Science, Environment, Ecoinformatics, and Education. CSEE 2011. Communications in Computer and Information Science, vol 215. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-23324-1_27
Download citation
DOI: https://doi.org/10.1007/978-3-642-23324-1_27
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-23323-4
Online ISBN: 978-3-642-23324-1
eBook Packages: Computer ScienceComputer Science (R0)