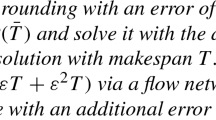Skip to main content
Springer Nature Link
Log in

On the Configuration-LP for Scheduling on Unrelated Machines

  • Conference paper
Algorithms – ESA 2011 (ESA 2011)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 6942))

Included in the following conference series:

  • 2778 Accesses

Abstract

Closing the approximability gap between 3/2 and 2 for the minimum makespan problem on unrelated machines is one of the most important open questions in scheduling. Almost all known approximation algorithms for the problem are based on linear programs (LPs). In this paper, we identify a surprisingly simple class of instances which constitute the core difficulty for LPs: the so far hardly studied unrelated graph balancing case in which each job can be assigned to at most two machines. We prove that already for this basic setting the strongest known LP-formulation – the configuration-LP – has an integrality gap of 2, matching the best known approximation factor for the general case. This points towards an interesting direction of future research. The result is shown by a sophisticated construction of instances, based on deep insights on two key weaknesses of the configuration-LP.

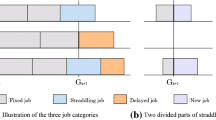
For the objective of maximizing the minimum machine load in the unrelated graph balancing setting we present an elegant purely combinatorial 2-approximation algorithm with only quadratic running time. Our algorithm uses a novel preprocessing routine that estimates the optimal value as good as the configuration-LP. This improves on the computationally costly LP-based (2 + ε)-approximation algorithm by Chakrabarty et al. [6].

This work was partially supported by Berlin Mathematical School (BMS) and by the DFG Focus Program 1307 within the project “Algorithm Engineering for Real-time Scheduling and Routing”.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Asadpour, A., Feige, U., Saberi, A.: Santa claus meets hypergraph matchings. In: Goel, A., Jansen, K., Rolim, J.D.P., Rubinfeld, R. (eds.) APPROX and RANDOM 2008. LNCS, vol. 5171, pp. 10–20. Springer, Heidelberg (2008)

    Google Scholar 

  2. Asadpour, A., Feige, U., Saberi, A.: Santa claus meets hypergraph matchings. Technical report, Standford University (2009), Available for download at http://www.stanford.edu/~asadpour/publication.htm

  3. Asadpour, A., Saberi, A.: An approximation algorithm for max-min fair allocation of indivisible goods. In: Proceedings of the 39th annual ACM symposium on Theory of computing (STOC 2007), pp. 114–121 (2007)

    Google Scholar 

  4. Bansal, N., Sviridenko, M.: The santa claus problem. In: Proceedings of the 38th Annual ACM Symposium on Theory of Computing (STOC 2006), pp. 31–40 (2006)

    Google Scholar 

  5. Bateni, M., Charikar, M., Guruswami, V.: Maxmin allocation via degree lower-bounded arborescences. In: Proceedings of the 41st Annual ACM Symposium on Theory of Computing (STOC 2009), pp. 543–552 (2009)

    Google Scholar 

  6. Chakrabarty, D., Chuzhoy, J., Khanna, S.: On allocating goods to maximize fairness. In: Proceedings of the 50th Annual Symposium on Foundations of Computer Science (FOCS 2009), pp. 107–116 (2009)

    Google Scholar 

  7. Correa, J.R., Skutella, M., Verschae, J.: The power of preemption on unrelated machines and applications to scheduling orders. In: Dinur, I., Jansen, K., Naor, J., Rolim, J. (eds.) APPROX 2009. LNCS, vol. 5687, pp. 84–97. Springer, Heidelberg (2009)

    Chapter  Google Scholar 

  8. Ebenlendr, T., Krčál, M., Sgall, J.: Graph balancing: a special case of scheduling unrelated parallel machines. In: Proceedings of the 19th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2008), pp. 483–490 (2008)

    Google Scholar 

  9. Eisenbrand, F., Palvoelgyi, D., Rothvoss, T.: Bin packing via discrepancy of permutations. In: Proceedings of the 22th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2011), pp. 476–481 (2011)

    Google Scholar 

  10. Feige, U.: On allocations that maximize fairness. In: Proceedings of the 19th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2008), pp. 287–293 (2008)

    Google Scholar 

  11. Gairing, M., Monien, B., Woclaw, A.: A faster combinatorial approximation algorithm for scheduling unrelated parallel machines. Theoretical Computer Science 380, 87–99 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  12. Haeupler, B., Saha, B., Srinivasan, A.: New constructive aspects of the lovasz local lemma. In: Proceedings of the 51st Annual IEEE Symposium on Foundations of Computer Science (FOCS 2010), pp. 397–406 (2010)

    Google Scholar 

  13. Karmarkar, N., Karp, R.M.: An efficient approximation scheme for the one-dimensional bin-packing problem. In: Proceedings of the 23rd Annual IEEE Symposium on Foundations of Computer Science (FOCS 1982), pp. 312–320 (1982)

    Google Scholar 

  14. Lawler, E.L., Labetoulle, J.: On preemptive scheduling of unrelated parallel processors by linear programming. Journal of the ACM 25, 612–619 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  15. Lee, K., Leung, J.Y., Pinedo, M.L.: A note on graph balancing problems with restrictions. Information Processing Letters 110, 24–29 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lenstra, J.K., Shmoys, D.B., Tardos, E.: Approximation algorithms for scheduling unrelated parallel machines. Mathematical Programming 46, 259–271 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  17. Leung, J.Y., Li, C.: Scheduling with processing set restrictions: A survey. International Journal of Production Economics 116, 251–262 (2008)

    Article  Google Scholar 

  18. Lin, Y., Li, W.: Parallel machine scheduling of machine-dependent jobs with unit-length. European Journal of Operational Research 156, 261–266 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  19. Scheithauer, G., Terno, J.: Theoretical investigations on the modified integer round-up property for the one-dimensional cutting stock problem. Operations Research Letters 20, 93–100 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  20. Schuurman, P., Woeginger, G.J.: Polynomial time approximation algorithms for machine scheduling: Ten open problems. Journal of Scheduling 2, 203–213 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  21. Shchepin, E.V., Vakhania, N.: An optimal rounding gives a better approximation for scheduling unrelated machines. Operations Research Letters 33, 127–133 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  22. Shmoys, D.B., Tardos, E.: An approximation algorithm for the generalized assignment problem. Mathematical Programming 62, 461–474 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  23. Svensson, O.: Santa claus schedules jobs on unrelated machines. In: Proceedings of the 43th Annual ACM Symposium on Theory of Computing, STOC 2011 (2011) (to appear)

    Google Scholar 

  24. Verschae, J., Wiese, A.: On the configuration-LP for scheduling on unrelated machines. Technical Report 025-2010, Technische Universität Berlin (November 2010)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Technische Universität Berlin, Straße des 17. Juni 136, 10623, Berlin, Germany

    José Verschae & Andreas Wiese

Authors
  1. José Verschae
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andreas Wiese
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Dipartimento di Informatica e Sistemistica, University of Rome " La Sapienza", via Ariosto 25, 00185, Roma, Italy

    Camil Demetrescu

  2. School of Computer Science, Reykjavik University, Menntavegur 1, 101, Reykjavik, Iceland

    Magnús M. Halldórsson

Rights and permissions

Reprints and permissions

Copyright information

© 2011 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Verschae, J., Wiese, A. (2011). On the Configuration-LP for Scheduling on Unrelated Machines. In: Demetrescu, C., Halldórsson, M.M. (eds) Algorithms – ESA 2011. ESA 2011. Lecture Notes in Computer Science, vol 6942. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-23719-5_45

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-23719-5_45

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-23718-8

  • Online ISBN: 978-3-642-23719-5

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics