Skip to main content
Springer Nature Link
Log in

An Output-Sensitive Approach for the L 1/L  ∞  k-Nearest-Neighbor Voronoi Diagram

  • Conference paper
Algorithms – ESA 2011 (ESA 2011)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 6942))

Included in the following conference series:

  • 2701 Accesses

Abstract

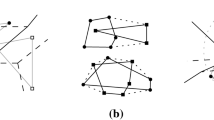
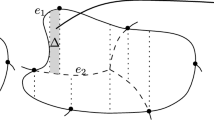
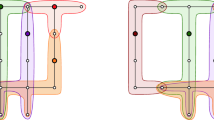
This paper revisits the k-nearest-neighbor (k-NN) Voronoi diagram and presents the first output-sensitive paradigm for its construction. It introduces the k-NN Delaunay graph, which corresponds to the graph theoretic dual of the k-NN Voronoi diagram, and uses it as a base to directly compute the k-NN Voronoi diagram in R 2. In the L 1, L  ∞  metrics this results in O((n + m)logn) time algorithm, using segment-dragging queries, where m is the structural complexity (size) of the k-NN Voronoi diagram of n point sites in the plane. The paper also gives a tighter bound on the structural complexity of the k-NN Voronoi diagram in the L  ∞  (equiv. L 1) metric, which is shown to be O(min{k(n − k), (n − k)2}).

This work was performed while the first and third authors visited University of Lugano in September/October 2010. It was supported in part by the University of Lugano during the visit, by the Swiss National Science Foundation under grant SNF-200021-127137, and by the National Science Council, Taiwan under grants No. NSC-98-2221-E-001-007-MY3, No. NSC-98-2221-E-001-008-MY3, and No. NSC-99-2918-I-001-009.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Abellanas, M., Bose, P., Garcia, J., Hurtado, F., Nicolas, C.M., Ramos, P.A.: On structural and graph theoretic properties of higher order Delaunay graphs. Internat. J. Comput. Geom. Appl. 19(6), 595–615 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  2. Agarwal, P.K., de Berg, M., Matousek, J., Schwarzkopf, I.: Constructing levels in arrangements and higher order Voronoi diagrams. Siam J. on Computing 27(3), 654–667 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  3. Aggarwal, A., Guibas, L.J., Saxe, J., Shor, P.W.: A linear-time algorithm for computing Voronoi diagram of a convex polygon. Discrete and Computational Geometry 4, 591–604 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  4. Aurenhammer, F., Klein, R.: Voronoi Diagrams. In: Handbook of Computational Geometry. Elseiver, Amsterdam (2000)

    Google Scholar 

  5. Aurenhammer, F., Schwarzkopf, O.: A simple on-line randomized incremental algorithm for computing higher order Voronoi diagrams. Internat. J. Comput. Geom. Appl. 2, 363–381 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  6. Boissonnat, J.D., Devillers, O., Teillaud, M.: A semidynamic construction of higher-order Voronoi diagrams and its randomized analysis. Algorithmia 9, 329–356 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chazelle, B.: An algorithm for segment dragging and its implementation. Algorithmica 3, 205–221 (1988)

    Article  MathSciNet  Google Scholar 

  8. Chazelle, B., Edelsbrunner, H.: An improved algorithm for constructing kth-order Voronoi Diagram. IEEE Trans. on Computers 36(11), 1349–1454 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  9. Clarkson, K.L.: New applications of random sampling in computational geometry. Discrete and Computational Geometry 2, 195–222 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  10. Clarkson, K.L., Shor, P.W.: Applications of random sampling in computational geometry, II. Discrete and Computational Geometry 4, 387–421 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  11. Edelsbrunner, H., O’Rourke, J., Seidel, R.: Constructing arrangements of lines and hyperplanes with applications. SIAM J. on Computing 15, 341–363 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gudmundsson, J., Hammar, M., van Kreveld, M.: Higher order Delaunay triangulations. Computaional Geometry 23(1), 85–98 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hanan, M.: On Steiner’s problem with rectilinear distance. SIAM J. on Applied Mathematics 14, 255–265 (1966)

    Article  MathSciNet  MATH  Google Scholar 

  14. Lee, D.-T.: On k-nearest neighbor Voronoi Diagrams in the plane. IEEE Trans. on Computers 31(6), 478–487 (1982)

    MathSciNet  MATH  Google Scholar 

  15. Mitchell, J.S.B.: L1 Shortest Paths Among Polygonal Obstacles in the Plane. Algorithmica 8, 55–88 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  16. Mulmuley, K.: On levels in arrangements and Voronoi diagrams. Discrete and Computational Geometry 6, 307–338 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  17. Papadopoulou, E.: Critical Area computation for missing material defects in VLSI circuits. IEEE Trans. on CAD 20(5), 583–597 (2001)

    Article  MathSciNet  Google Scholar 

  18. Papadopoulou, E.: Net-aware Critical area extraction for opens in VLSI circuits via higher-order Voronoi diagrams. IEEE Trans. on CAD 30(5), 704–716 (2011)

    Article  Google Scholar 

  19. Papadopoulou, E., Lee, D.-T.: The L  ∞  Voronoi Diagram of Segments and VLSI Applications. Internat. J. Comput. Geom. Appl. 11(5), 503–528 (2001)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Research Center for Information Technology Innovation, Academia Sinica, Taiwan

    Chih-Hung Liu & D. T. Lee

  2. Faculty of Informatics, University of Lugano, Lugano, Switzerland

    Evanthia Papadopoulou

  3. Institute of Information Science, Academia Sinica, Taipei, Taiwan

    D. T. Lee

Authors
  1. Chih-Hung Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Evanthia Papadopoulou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. D. T. Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Dipartimento di Informatica e Sistemistica, University of Rome " La Sapienza", via Ariosto 25, 00185, Roma, Italy

    Camil Demetrescu

  2. School of Computer Science, Reykjavik University, Menntavegur 1, 101, Reykjavik, Iceland

    Magnús M. Halldórsson

Rights and permissions

Reprints and permissions

Copyright information

© 2011 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Liu, CH., Papadopoulou, E., Lee, D.T. (2011). An Output-Sensitive Approach for the L 1/L  ∞  k-Nearest-Neighbor Voronoi Diagram. In: Demetrescu, C., Halldórsson, M.M. (eds) Algorithms – ESA 2011. ESA 2011. Lecture Notes in Computer Science, vol 6942. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-23719-5_7

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-23719-5_7

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-23718-8

  • Online ISBN: 978-3-642-23719-5

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics