Variable Independence and Resolution Paths for Quantified Boolean Formulas

Abstract

Variable independence in quantified boolean formulas (QBFs) informally means that the quantifier structure of the formula can be rearranged so that two variables reverse their outer-inner relationship without changing the value of the QBF. Samer and Szeider introduced the standard dependency scheme and the triangle dependency scheme to safely over-approximate the set of variable pairs for which an outer-inner reversal might be unsound (JAR 2009).

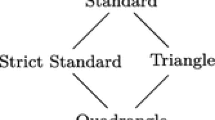
This paper introduces resolution paths and defines the resolution-path dependency relation. The resolution-path relation is shown to be the root (smallest) of a lattice of dependency relations that includes quadrangle dependencies, triangle dependencies, strict standard dependencies, and standard dependencies. Soundness is proved for resolution-path dependencies, thus proving soundness for all the descendants in the lattice.

It is shown that the biconnected components (BCCs) and block trees of a certain clause-literal graph provide the key to computing dependency pairs efficiently for quadrangle dependencies. Preliminary empirical results on the 568 QBFEVAL-10 benchmarks show that in the outermost two quantifier blocks quadrangle dependency relations are smaller than standard dependency relations by widely varying factors.