Optimization of Chaotic Micromixers Using Finite Time Lyapunov Exponents

Abstract

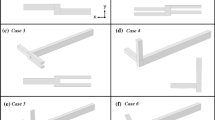
In microfluidics mixing of different fluids is a highly non-trivial task due to the absence of turbulence. The dominant process allowing mixing at low Reynolds number is therefore diffusion, thus rendering mixing in plain channels very inefficient. Recently, passive chaotic micromixers such as the staggered herringbone mixer were developed, allowing efficient mixing of fluids by repeated stretching and folding of the fluid interfaces. The optimization of the geometrical parameters of such mixer devices is often performed by time consuming and expensive trial and error experiments. We demonstrate that the application of the lattice Boltzmann method to fluid flow in highly complex mixer geometries together with standard techniques from statistical physics and dynamical systems theory can lead to a highly efficient way to optimize micromixer geometries. The strategy applies massively parallel fluid flow simulations inside a mixer, where massless and non-interacting tracer particles are introduced. By following their trajectories we can calculate finite time Lyapunov exponents in order to quantify the degree of chaotic advection inside the mixer. The current report provides a review of our results published in (Sarkar, Narváez, and Harting, 2010) together with additional details on the simulation methodology.