Abstract
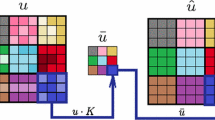
In this work we propose an image reduction algorith based on local reduction operators. We analyze the construction of weak local reduction operators by means of aggregation functions and we analyze the effect of several aggregation functions in image reduction with original and noisy images.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Beliakov, G., Pradera, A., Calvo, T.: Aggregation Functions: A Guide for Practitioners. Studies in Fuzziness and Soft Computing, vol. 221 (2007)
Bustince, H., Pagola, M., Barrenechea, E.: Construction of fuzzy indices from DI-subsethood measures: Application to the global comparison of images. Information Sciences 177, 906–929 (2007)
Bustince, H., Barrenechea, E., Pagola, M., Fernandez, J.: Interval-valued fuzzy sets constructed from matrices: Application to edge detection. Fuzzy Sets and Systems 160, 1819–1840 (2009)
Bustince, H., Calvo, T., De Baets, B., Fodor, J., Mesiar, R., Montero, J., Paternain, D., Pradera, A.: A class of aggregation functions encompassing two-dimensional OWA operators. Information Sciences 180, 1977–1989 (2010)
Calvo, T., Beliakov, G.: Aggregation functions based on penalties. Fuzzy sets and Systems 161, 1420–1436 (2010)
Chaira, T., Ray, A.K.: Fuzzy measures for color image retrieval. Fuzzy Sets and Systems 150, 545–560 (2005)
Fodor, J., Roubens, M.: Fuzzy Preference Modelling and Multicriteria Decision Support. Kluwer Academic Publishers, Dordrecht (1994)
Jurio, A., Pagola, M., Mesiar, R., Beliakov, G., Bustince, H.: Image magnification using interval information. IEEE Transactions on Image Processing (to appear)
Loia, V., Sessa, S.: Fuzzy relation equations for coding/decoding processes of images and videos. Information Sciences 171, 145–172 (2005)
Di Martino, F., Loia, V., Sessa, S.: A segmentation method for image compressed by fuzzy transform. Fuzzy Sets and Systems 161, 56–74 (2010)
Perfilieva, I.: Fuzzy Transforms and Their Applications to Image Compression. In: Bloch, I., Petrosino, A., Tettamanzi, A.G.B. (eds.) WILF 2005. LNCS (LNAI), vol. 3849, pp. 19–31. Springer, Heidelberg (2006)
Rückschlossová, T.: Aggregation operators and invariantness. PhD thesis, Slovak University of Technology, Bratislava, Slovakia (June 2003)
Rückschlossová, T., Rückschloss, R.: Homogeneous aggregation operators. Kybernetika (Prague) 42(3), 279–286 (2006)
Unser, M., Aldroubi, A., Eden, M.: Enlargement or reduction of digital images with minimum loss of information. IEEE Transactions on Image Processing 4, 247–258 (1995)
Xiang, S., Nie, F., Zhang, C.: Learning a Mahalanobis distance metric for data clustering and classification. Pattern Recognition 41, 3600–3612 (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Paternain, D., Lopez-Molina, C., Bustince, H., Mesiar, R., Beliakov, G. (2011). Image Reduction Using Fuzzy Quantifiers. In: Melo-Pinto, P., Couto, P., Serôdio, C., Fodor, J., De Baets, B. (eds) Eurofuse 2011. Advances in Intelligent and Soft Computing, vol 107. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-24001-0_32
Download citation
DOI: https://doi.org/10.1007/978-3-642-24001-0_32
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-24000-3
Online ISBN: 978-3-642-24001-0
eBook Packages: EngineeringEngineering (R0)