Skip to main content
Springer Nature Link
Log in

Graph Classes with Structured Neighborhoods and Algorithmic Applications

  • Conference paper
Graph-Theoretic Concepts in Computer Science (WG 2011)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 6986))

Included in the following conference series:

  • 853 Accesses

Abstract

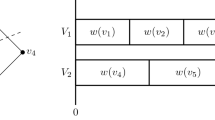
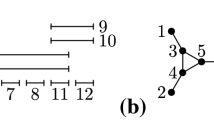
Boolean-width is a recently introduced graph width parameter. If a boolean decomposition of width w is given, several NP-complete problems, such as Maximum Weight Independent Set, k-Coloring and Minimum Weight Dominating Set are solvable in O *(2O(w)) time [6]. In this paper we study graph classes for which we can compute a decomposition of logarithmic boolean-width in polynomial time. Since 2O(logn) = n O(1), this gives polynomial time algorithms for the above problems on these graph classes. For interval graphs we show how to construct decompositions where neighborhoods of vertex subsets are nested. We generalize this idea to neighborhoods that can be represented by a constant number of vertices. Moreover we show that these decompositions have boolean-width O(logn). Graph classes having such decompositions include circular arc graphs, circular k-trapezoid graphs, convex graphs, Dilworth k graphs, k-polygon graphs and complements of k-degenerate graphs. Combined with results in [1,5], this implies that a large class of vertex subset and vertex partitioning problems can be solved in polynomial time on these graph classes.

This project was partially supported by the Research Council of Norway.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Adler, I., Bui-Xuan, B.-M., Rabinovich, Y., Renault, G., Telle, J.A., Vatshelle, M.: On the Boolean-Width of a Graph: Structure and Applications. In: Thilikos, D.M. (ed.) WG 2010. LNCS, vol. 6410, pp. 159–170. Springer, Heidelberg (2010)

    Chapter  Google Scholar 

  2. Brandstädt, A., Kratsch, D.: On the Restriction of Some np-Complete Graph Problems to Permutation Graphs. In: Budach, L. (ed.) FCT 1985. LNCS, vol. 199, pp. 53–62. Springer, Heidelberg (1985)

    Chapter  Google Scholar 

  3. Brandstädt, A., Le, V.B., Spinrad, J.P.: Graph classes: a survey (1999)

    Google Scholar 

  4. Brandstädt, A., Lozin, V.V.: On the linear structure and clique-width of bipartite permutation graphs. Ars Comb. 67 (2003)

    Google Scholar 

  5. Bui-Xuan, B.M., Telle, J.A., Vatshelle, M.: Fast algorithms for vertex subset and vertex partitioning problems on graphs of low boolean-width. arXiv

    Google Scholar 

  6. Bui-Xuan, B.-M., Telle, J.A., Vatshelle, M.: Boolean-Width of Graphs. In: Chen, J., Fomin, F.V. (eds.) IWPEC 2009. LNCS, vol. 5917, pp. 61–74. Springer, Heidelberg (2009)

    Chapter  Google Scholar 

  7. Chang, M.S.: Weighted Domination on Cocomparability Graphs. In: Staples, J., Katoh, N., Eades, P., Moffat, A. (eds.) ISAAC 1995. LNCS, vol. 1004, pp. 122–131. Springer, Heidelberg (1995)

    Chapter  Google Scholar 

  8. Chang, M.S.: Efficient algorithms for the domination problems on interval and circular-arc graphs. SIAM J. on Computing 27(6), 1671–1694 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  9. Corneil, D.G., Perl, Y.: Clustering and domination in perfect graphs. Discrete Applied Math. 9, 27–40 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  10. Courcelle, B., Makowsky, J.A., Rotics, U.: Linear time solvable optimization problems on graphs of bounded clique-width. Theory Comput. Syst. 33(2), 125–150 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  11. Damaschke, P., Müller, H., Kratsch, D.: Domination in convex and chordal bipartite graphs. Inf. Process. Lett. 36(5), 231–236 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  12. Díaz, J., Nešetřil, J., Serna, M., Thilikos, D.M.: H-Colorings of Large Degree Graphs. In: Shafazand, H., Tjoa, A.M. (eds.) EurAsia-ICT 2002. LNCS, vol. 2510, pp. 850–857. Springer, Heidelberg (2002)

    Chapter  Google Scholar 

  13. Elmallah, E.S., Stewart, L.K.: Independence and domination in polygon graphs. Discrete Appllied Math 44(1-3), 65–77 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  14. Farber, M., Keil, J.: Domination in permutation graphs. J. Algorithms 6, 309–321 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  15. Geelen, J.F., Gerards, B., Whittle, G.: Branch-width and well-quasi-ordering in matroids and graphs. J. Comb. Theory, Ser. B 84(2), 270–290 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  16. Golumbic, M.C., Rotics, U.: On the Clique-Width of Perfect Graph Classes Extended Abstract. In: Widmayer, P., Neyer, G., Eidenbenz, S. (eds.) WG 1999. LNCS, vol. 1665, pp. 135–147. Springer, Heidelberg (1999)

    Chapter  Google Scholar 

  17. van’t Hof, P., Paulusma, D., van Rooij, J.M.M.: Computing role assignments of chordal graphs. Theor. Comput. Sci. 411(40-42), 3601–3613 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. Hsu, W.L., Tsai, K.H.: Linear time algorithms on circular-arc graphs. Inf. Process. Lett. 40(3), 123–129 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  19. Jelínek, V.: The rank-width of the square grid. Discrete Applied Math 158(7), 841–850 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  20. Keil, J.M.: The complexity of domination problems in circle graphs. Discrete Applied Math. 42(1), 51–63 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  21. Kim, K.H.: Boolean matrix theory and its applications. Marcel Dekker (1982)

    Google Scholar 

  22. Kobler, D., Rotics, U.: Polynomial algorithms for partitioning problems on graphs with fixed clique-width (extended abstract). In: Proc. SODA, pp. 468–476 (2001)

    Google Scholar 

  23. Kratochvíl, J., Manuel, P.D., Miller, M.: Generalized domination in chordal graphs. Nord. J. Comput. 2(1), 41–50 (1995)

    MathSciNet  MATH  Google Scholar 

  24. Liang, Y.: Dominations in trapezoid graphs. Inf. Process. Lett. 52(6), 309–315 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  25. McConnell, R.M.: Linear-time recognition of circular-arc graphs. Algorithmica 37, 93–147 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  26. Oum, S., Seymour, P.D.: Approximating clique-width and branch-width. J. Comb. Theory, Ser. B 96(4), 514–528 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  27. Rhee, C., Liang, Y., Dhall, S., Lakshmivarahan, S.: An o(n + m)-time algorithm for finding a minimum-weight dominating set in a permutation graph. SIAM J. on Computing 25(2), 404–419 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  28. de Ridder, H.N., et al.: Information System on Graph Classes and their Inclusions (ISGCI), http://wwwteo.informatik.uni-rostock.de/isgci

  29. Robertson, N., Seymour, P.D.: Graph minors. X. obstructions to tree-decomposition. J. Comb. Theory, Ser. B 52(2), 153–190 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  30. Telle, J.A., Proskurowski, A.: Algorithms for vertex partitioning problems on partial k-trees. SIAM J. Discrete Math. 10(4), 529–550 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  31. Tsai, K.H., Hsu, W.L.: Fast algorithms for the dominating set problem on permutation graphs. Algorithmica 9(6), 601–614 (1993)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Informatics, University of Bergen, P.O. Box 7803, N-5020, Bergen, Norway

    Rémy Belmonte & Martin Vatshelle

Authors
  1. Rémy Belmonte
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Martin Vatshelle
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. KAM MFF UK, Charles University, Malostranské nám 25, 11800, Praha 1, Czech Republic

    Petr Kolman  & Jan Kratochvíl  & 

Rights and permissions

Reprints and permissions

Copyright information

© 2011 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Belmonte, R., Vatshelle, M. (2011). Graph Classes with Structured Neighborhoods and Algorithmic Applications. In: Kolman, P., Kratochvíl, J. (eds) Graph-Theoretic Concepts in Computer Science. WG 2011. Lecture Notes in Computer Science, vol 6986. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-25870-1_6

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-25870-1_6

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-25869-5

  • Online ISBN: 978-3-642-25870-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics