Abstract
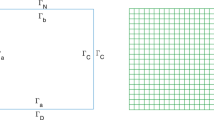
In this paper we present a finite element method (FEM) to a nonstandard second-order elliptic eigenvalue problem defined on a two-component domain consisting of two intervals with a contact point. This vector problem involves a nonlocal (integral type) coupling condition between the solution components. By introducing suitable degrees of freedom for the quadratic finite element and a corresponding vector Lagrange interpolant we derive optimal order finite element approximation.
Some numerical aspects concerning the method implementation are considered. Illustrative example is given which shows the efficiency of the proposed method.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Andreev, A.B., Racheva, M.R.: Superconvergence of the interpolated quadratic finite elements on triangular meshes. Math. Balkanica, New Series, vol.19, Fasc. 3–4, 385–404 (2005)
Galin, G.A.: Contact Problems: The Legacy of L.A. Galin. In: Gladwell, G.M.L. (ed.) Springer, Dordrecht (2008)
Ciarlet, P.: Basic Error Estimates for the FEM, vol. 2, pp. 17–35. Elsevier, Amsterdam (1991)
Lin, Q., Yan, N., Zhou, A.: A rectangle test for interpolated finite elements. In: Proceedings of Systems Science & Systems Engineering, pp. 217–229. Culture Publish Co. (1991)
Raviart, P.A., Thomas, J.M.: Introduction a l’Analyse Numerique des Equations aux Derivees Partielles, Masson Paris (1983)
De Shepper, H., Van Keer, R.: Finite Element Approximation of a Contact Vector Eigenvalue Problem. Applications of Mathematics 48(6), 559–571 (2003)
Shin, T.M.: Numerical Heat Transfer. Hemisphere Publ. Corp., Washington (1984)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Andreev, A.B., Racheva, M.R. (2012). Quadratic Finite Element Approximation of a Contact Eigenvalue Problem. In: Lirkov, I., Margenov, S., Waśniewski, J. (eds) Large-Scale Scientific Computing. LSSC 2011. Lecture Notes in Computer Science, vol 7116. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-29843-1_60
Download citation
DOI: https://doi.org/10.1007/978-3-642-29843-1_60
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-29842-4
Online ISBN: 978-3-642-29843-1
eBook Packages: Computer ScienceComputer Science (R0)