Reduced Large Datasets by Fuzzy C-Mean Clustering Using Minimal Enclosing Ball

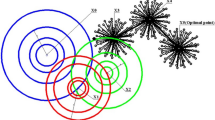
Abstract

Minimal Enclosing Ball (MEB) is a spherically shaped boundary around a normal dataset, it is used to separate this set from abnormal data. MEB has a limitation for dealing with a large dataset in which computational load drastically increases as training data size becomes large. To handle this problem in huge dataset used in different domains, we propose two approaches using Fuzzy C-mean clustering method. These approaches find the concentric balls with minimum volume of data description to reduce the chance of accepting abnormal data that contain most of the training samples. Our method uses a divide-and-conquer strategy; trains each decomposed sub-problems to get support vectors and retrains with the support vectors to find a global data description of a whole target class. Our study is experimented on speech information to eliminate all noise data and reducing time training. For this, the training data, learned by Support Vector Machines (SVMs), is partitioned among several data sources. Computation of such SVMs can be achieved by finding a core-set for the image of the data. Numerical experiments on some real-world datasets verify the usefulness of our approaches for data mining.