Abstract
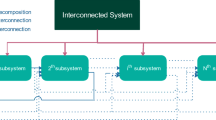
Based on the inclusion principle, a judging method of connective stability is presented for a class of linear interconnected large-scale systems. First, the system is decomposed into a group of subsystems. Through stability analysis and judgment of each subsystem, a group of judgment matrices are obtained. After being permuted and corrected, these judgment matrices can be composed an extended judgment matrix. According to the constraints conditions of inclusion principle, it can be contracted into a judgment matrix. If the judgment matrix is diagonally dominant and an M-matrix, then the system is connective stable. Parameters of judgment matrices are derived from each subsystem, which are easy to be obtained. Finally, it takes an example to show that the method is of the validity.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Šiljak, D.D.: Decentralized Control of Complex Systems. Academic Press, Boston (1991)
Wu, L., He, J.: Connective Stability of Impulsive Large-scale Systems. In: Proceedings of Chinese Control and Decision Conference, pp. 66–71. Northeastern University Press, Shenyang (1994)
Liu, K., Qian, L.: Connective Stability of Uncertain Discrete Large-scale Systems. In: Proceedings of Chinese Control Conference, pp. 236–239. Chinese Science and Technology Press, Beijing (1996)
Nian, X., Li, X., Yang, Y., Zhuo, Z.: A BMI Approach to the Absolute Connective Stability of Lurie Control Systems. In: Proceedings of the 23rd Chinese Control Conference, pp. 1462–1466. East China University of Science and Technology Press, Shanghai (2004)
Nian, X., Cao, L.: BMI Approach to the Interconnected Stability and Cooperative Control of Linear Systems. ACTA Automatic Sinica 34(4), 438–444 (2008)
Deng, X., Nian, X., Pan, H.: Connective Stability and Cooperative Control of Linear Time-delay Systems. Control Theory and Applications 27(11), 1504–1510 (2010)
Chen, X.B., Stankovic, S.S.: Decomposition and Decentralized Control of Systems with Multi-overlapping Structure. Automatica 41, 1765–1772 (2005)
Chen, X.B., Stankovic, S.S.: Overlapping Decentralized Approach to Automation Generation Control of Multi-area Power Systems. International Journal of Control 80(3), 386–402 (2007)
Šiljak, D.D.: Dynamic Graphs. Nonlinear Analysis: Hybrid Systems 2, 544–567 (2008)
Ouyang, X., Chen, X.B.: Modeling and Decomposition of Complex Dynamic Interconnected Systems. International Journal of Information and Systems Sciences 5(2), 248–259 (2009)
Ouyang, X., Chen, X.B.: Inclusion Principle for Dynamic Graphs. In: Tan, Y., Shi, Y., Chai, Y., Wang, G. (eds.) ICSI 2011, Part II. LNCS, vol. 6729, pp. 449–456. Springer, Heidelberg (2011)
Kadaiche, M., Habbit, H., Zelmat, M.: Stability of Interconnected Systems under Structural Perturbation: Decomposition Aggregation Approach. World Academy of Science, Engineering and Technology 37, 335–339 (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Chen, X., Lu, X., Ouyang, X., Xiao, X. (2012). Connective Stability Analysis for a Class of Large-Scale Systems Based on the Inclusion Principle. In: Tan, Y., Shi, Y., Ji, Z. (eds) Advances in Swarm Intelligence. ICSI 2012. Lecture Notes in Computer Science, vol 7332. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-31020-1_59
Download citation
DOI: https://doi.org/10.1007/978-3-642-31020-1_59
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-31019-5
Online ISBN: 978-3-642-31020-1
eBook Packages: Computer ScienceComputer Science (R0)