Abstract
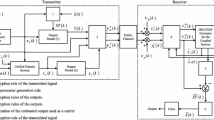
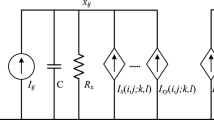
In this paper, the problem of synchronization of CNN(Cellular Neural Network) hyperchaotic system is studied. The hyperchaotic system has very strong random and inscrutability and make use of its multiple state variables to encrypt the information signal, therefore having higher security. Based on state observer, we realize the synchronization of the CNN hyperchaotic system. The synchronization theory is applied in the two-channel secure communication. Finally, we put forward a new six order CNN hyperchaotic system in simulation. The synchronization results verify the correctness of the theory. The secure communication simulation demonstrates the effectiveness of the method.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
References
Pecora, L., Carrol, T.: Synchronization chaotic system. Physics Review Letter 64, 821–826 (1990)
Zhang, Q., Lu, J.: An Chaos synchronization of a new chaotic system via nonlinear control. Chaos, Solitons and Fractals 37, 175–179 (2008)
Lian, K.: Adaptive synchronization design for chaotic system via a scalar driving signal. IEEE Trans. on Circuit System I: Fundamental Theory and Applications 49, 17–27 (2002)
He, H., Tu, J., Xiong, P.: Lr-synchronization and adaptive synchronization of a class of chaotic Lurie systems under perturbations. Journal of the Franklin Institute 348, 2257–2269 (2011)
Sun, H., Cao, H.: Chaos control and synchronization of a modified chaotic system. Chaos Solitons and Fractals 37, 1442–1455 (2008)
Tu, J., He, H.: Guaranteed cost synchronization of chaotic cellular neural networks with time-varying delay. Neural Computation 24, 217–233 (2012)
Tu, J., He, H., Xiong, P.: Guaranteed cost synchronous control of time-varying delay cellular neural networks. Neural Computing and Application (2011), doi:10.1007/s00521-011-0667-6
Liu, J., Lu, J., Dou, X.: State observer design for a class of more general Lipschitz nonlinear systems. Journal of Systems Engineering 26, 161–165 (2011)
Ming, T., Zhang, Y., Sun, Y., Zhang, X.: A new design method of state observer for Lipschitz nonlinear systems. Journal of Naval University 20, 105–108 (2008)
Lang, M., Xu, M.: Observer design for a chaos of nonlinear systems. Natural Sciences Journal of Harbin Normal University 26, 50–53 (2010)
Yan, L., He, H., Xiong, P.: Algebraic condition of control for multiple time-delayed chaotic cellular neural networks. In: Fourth International Workshop Intelligence of Computational of on Advanced, pp. 604–608 (2011)
Alexandre, C., Correa, L., Zhao, L.: Design of associative memories using cellular neural networks. Neurocomputing 72, 2180–2188 (2009)
Wang, S., Chung, K., Duan, F.: Applying the to white blood cell of the improved fuzzy cellular neural network IF CNN detection. Neurocomputing 7, 1348–1359 (2007)
Milanova, M., Ulrich, B.: Object the recognition in image sequences with cellular neural networks. Neurocomputing 31, 125–141 (2000)
Jiang, G., Wang, S.: Synchronization of hyperchaos of cellular neural network with applications to secure communication. Journal of China Institute of Communications 21, 82–85 (2000)
Zhao, L., Li, X., Zhao, G.: Secure communication based on synchronized hyperchaos of cellular neural network. Journal of Circuits and Systems 8, 42–44 (2003)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Wang, XD., Li, WJ., Xiong, P. (2012). CNN Hyperchaotic Synchronization with Applications to Secure Communication. In: Wang, J., Yen, G.G., Polycarpou, M.M. (eds) Advances in Neural Networks – ISNN 2012. ISNN 2012. Lecture Notes in Computer Science, vol 7368. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-31362-2_68
Download citation
DOI: https://doi.org/10.1007/978-3-642-31362-2_68
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-31361-5
Online ISBN: 978-3-642-31362-2
eBook Packages: Computer ScienceComputer Science (R0)