Abstract
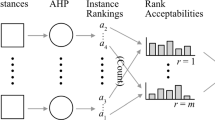
In this paper, we extend the Choquet integral decision model in the same spirit of the Stochastic Multicriteria Acceptability Analysis (SMAA) method that takes into account a probability distribution over the preference parameters of multiple criteria decision methods. In order to enrich the set of parameters (the capacities) compatible with the DM’s preference information on the importance of criteria and interaction between couples of criteria, we put together Choquet integral with SMAA. The sampling of the compatible preference parameters (the capacities) is obtained by a Hit-and-Run procedure. Finally, we evaluate a set of capacities contributing to the evaluation of the rank acceptability indices and of the central preference parameters as done in the SMAA methods.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Angilella, S., Greco, S., Lamantia, F., Matarazzo, B.: Assessing non-additive utility for multicriteria decision aid. European Journal of Operational Research 158(3), 734–744 (2004)
Angilella, S., Greco, S., Matarazzo, B.: Non-additive robust ordinal regression: A multiple criteria decision model based on the choquet integral. European Journal of Operational Research 201(1), 277–288 (2010)
Bana e Costa, C.A.: A multicriteria decision aid methodology to deal with conflicting situations on the weights. European Journal of Operational Research 26(1), 22–34 (1986)
Bana e Costa, C.A.: A methodology for sensitivity analysis in three-criteria problems: A case study in municipal management. European Journal of Operational Research 33(2), 159–173 (1988)
Chateauneuf, A., Jaffray, J.Y.: Some characterizations of lower probabilities and other monotone capacities through the use of möbius inversion. Mathematical Social Sciences 17, 263–283 (1989)
Choquet, G.: Theory of capacities. Ann. Inst. Fourier 5(54), 131–295 (1953)
Figueira, J., Greco, S., Ehrgott, M.: Multiple Criteria Decision Analysis: State of the Art Surveys. Springer, Berlin (2010)
Gilboa, I., Schmeidler, D.: Additive representations of non-additive measures and the choquet integral. Ann. Operational Research 52, 43–65 (1994)
Grabisch, M.: The application of fuzzy integrals in multicriteria decision making. European Journal of Operational Research 89, 445–456 (1996)
Grabisch, M.: k-order additive discrete fuzzy measures and their representation. Fuzzy Sets and Systems 92, 167–189 (1997)
Greco, S., Matarazzo, B., Giove, S.: The Choquet integral with respect to a level dependent capacity. Fuzzy Sets and Systems 175, 1–35 (2011)
Greco, S., Mousseau, V., Słowiński, R.: Ordinal regression revisited: multiple criteria ranking using a set of additive value functions. European Journal of Operational Research 191(2), 416–436 (2008)
Keeney, R.L., Raiffa, H.: Decisions with multiple objectives: Preferences and value tradeoffs. J. Wiley, New York (1976)
Lahdelma, R., Hokkanen, J., Salminen, P.: SMAA - stochastic multiobjective acceptability analysis. European Journal of Operational Research 106(1), 137–143 (1998)
Lahdelma, R., Salminen, P.: SMAA-2: Stochastic multicriteria acceptability analysis for group decision making. Operations Research 49(3), 444–454 (2001)
Marichal, J.L., Roubens, M.: Determination of weights of interacting criteria from a reference set. European Journal of Operational Research 124(3), 641–650 (2000)
Murofushi, S., Soneda, T.: Techniques for reading fuzzy measures (iii): interaction index. In: 9th Fuzzy Systems Symposium, Sapporo, Japan, pp. 693–696 (1993)
Barba Romero, S., Pomerol, J.C.: Choix multicritère dans l’enterprise. Heres. Collection Informatique (1993)
Rota, G.C.: On the foundations of combinatorial theory i. Theory of möbius functions. Wahrscheinlichkeitstheorie und Verwandte Gebiete 2, 340–368 (1964)
Shafer, G.: A Mathematical Theory of Evidence. Princeton University Press (1976)
Shapley, L.S.: A value for n-person games. In: Tucker, A.W., Kuhn, H.W. (eds.) Contributions to the Theory of Games II, p. 307. Princeton University Press, Princeton (1953)
Smith, R.L.: Efficient Monte Carlo procedures for generating points uniformly distributed over bounded regions. Operations Research 32, 1296–1308 (1984)
Tervonen, T., Figueira, J.: A survey on stochastic multicriteria acceptability analysis methods. Journal of Multi-Criteria Decision Analysis 15(1-2), 1–14 (2008)
Tervonen, T., Van Valkenhoef, G., Basturk, N., Postmus, D.: Efficient weight generation for simulation based multiple criteria decision analysis. In: EWG-MCDA, Tarragona, April 12-14 (2012)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Angilella, S., Corrente, S., Greco, S. (2012). SMAA-Choquet: Stochastic Multicriteria Acceptability Analysis for the Choquet Integral. In: Greco, S., Bouchon-Meunier, B., Coletti, G., Fedrizzi, M., Matarazzo, B., Yager, R.R. (eds) Advances in Computational Intelligence. IPMU 2012. Communications in Computer and Information Science, vol 300. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-31724-8_26
Download citation
DOI: https://doi.org/10.1007/978-3-642-31724-8_26
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-31723-1
Online ISBN: 978-3-642-31724-8
eBook Packages: Computer ScienceComputer Science (R0)