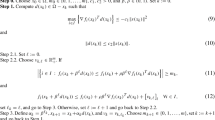Skip to main content
Springer Nature Link
Log in

Set Oriented Methods for the Numerical Treatment of Multiobjective Optimization Problems

  • Chapter
EVOLVE- A Bridge between Probability, Set Oriented Numerics and Evolutionary Computation

Part of the book series: Studies in Computational Intelligence ((SCI,volume 447))

Abstract

In many applications, it is required to optimize several conflicting objectives concurrently leading to a multobjective optimization problem (MOP). The solution set of a MOP, the Pareto set, typically forms a (k-1)-dimensional object, where k is the number of objectives involved in the optimization problem. The purpose of this chapter is to give an overview of recently developed set oriented techniques - subdivision and continuation methods - for the computation of Pareto sets \(\mathcal{P}\) of a givenMOP. All these methods have in common that they create sequences of box collections which aim for a tight covering of \(\mathcal{P}\). Further, we present a class of multiobjective optimal control problems which can be efficiently handled by the set oriented continuation methods using a transformation into high-dimensionalMOPs. We illustrate all the methods on both academic and real world examples.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Allgower, E.L., Georg, K.: Numerical Continuation Methods. Springer (1990)

    Google Scholar 

  2. Betts, J.T.: Survey of numerical methods for trajectory optimization. AIAA J. Guidance, Control, and Dynamics 21(2), 193–207 (1998)

    Article  MATH  Google Scholar 

  3. Binder, T., Blank, L., Bock, H.G., Bulirsch, R., Dahmen, W., Diehl, M., Kronseder, T., Marquardt, W., Schlöder, J.P., von Stryk, O.: Introduction to model based optimization of chemical processes on moving horizons. In: Grötschel, M., Krumke, S.O., Rambau, J. (eds.) Online Optimization of Large Scale Systems: State of the Art, pp. 295–340. Springer (2001)

    Google Scholar 

  4. Blesken, M., Rückert, U., Steenken, D., Witting, K., Dellnitz, M.: Multiobjective Optimization for Transistor Sizing of CMOS Logic Standard Cells Using Set-Oriented Numerical Techniques. In: 27th Norchip Conference (2009)

    Google Scholar 

  5. Bosman, P.A.N., de Jong, E.D.: Exploiting gradient information in numerical multi-objective evolutionary optimization. In: Genetic and Evolutionary Computation Conference - GECCO 2005. ACM (2005)

    Google Scholar 

  6. Coello Coello, C.A., Lamont, G.B., Van Veldhuizen, D.A.: Evolutionary Algorithms for Solving Multi-Objective Problems, 2nd edn. Springer, New York (2007) ISBN 978-0-387-33254-3

    MATH  Google Scholar 

  7. Das, I., Dennis, J.: Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM Journal of Optimization 8, 631–657 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  8. Deb, K.: Multi-Objective Optimization using Evolutionary Algorithms. John Wiley & Sons, Chichester (2001) ISBN 0-471-87339-X

    MATH  Google Scholar 

  9. Dell’Aere, A.: Multi-objective optimization in self-optimizing systems. In: Proceedings of the IEEE 32nd Annual Conference on Industrial Electronics (IECON), pp. 4755–4760 (2006)

    Google Scholar 

  10. Dell’Aere, A.: Numerical methods for the solution of bi-level multi-objective optimization problems. PhD thesis. University of Paderborn, Germany (2008)

    Google Scholar 

  11. Dellnitz, M., Hohmann, A.: The computation of unstable manifolds using subdivision and continuation. In: Broer, H.W., van Gils, S.A., Hoveijn, I., Takens, F. (eds.) Nonlinear Dynamical Systems and Chaos, vol. 19, pp. 449–459. PNLDE, Birkhäuser (1996)

    Google Scholar 

  12. Dellnitz, M., Hohmann, A.: A subdivision algorithm for the computation of unstable manifolds and global attractors. Numerische Mathematik 75, 293–317 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  13. Dellnitz, M., Ober-Blöbaum, S., Post, M., Schütze, O., Thiere, B.: A multi-objective approach to the design of low thrust space trajectories using optimal control. Celestial Mechanics and Dynamical Astronomy 105(1), 33–59 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  14. Dellnitz, M., Schütze, O., Hestermeyer, T.: Covering Pareto sets by multilevel subdivision techniques. Journal of Optimization Theory and Applications 124, 113–155 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  15. Dellnitz, M., Schütze, O., Sertl, S.: Finding zeros by multilevel subdivision techniques. IMA Journal of Numerical Analysis 22(2), 167–185 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  16. Eichfelder, G.: Adaptive Scalarization Methods in Multiobjective Optimization. Springer, Heidelberg (2008) ISBN 978-3-540-79157-7

    Book  MATH  Google Scholar 

  17. Fliege, J.: Gap-free computation of Pareto-points by quadratic scalarizations. Mathematical Methods of Operations Research 59, 69–89 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  18. Fliege, J., Fux Svaiter, B.: Steepest descent methods for multicriteria optimization. Mathematical Methods of Operations Research 51(3), 479–494 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  19. Fliess, M., Levine, J., Martin, P., Rouchon, P.: Flatness and defect of non-linear systems: Introductory theory and examples. International Journal of Control 61(6), 1327–1361 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  20. Gandibleux, X.: Metaheuristics for Multiobjective Optimisation. Lecture notes in economics and mathematical systems. Springer (2004)

    Google Scholar 

  21. Geisler, J., Witting, K., Trächtler, A., Dellnitz, M.: Multiobjective optimization of control trajectories for the guidance of a rail-bound vehicle. In: 17th IFAC World Congress, Seoul, Korea, July 6-11 (2008)

    Google Scholar 

  22. Geisler, J., Witting, K., Trächtler, A., Dellnitz, M.: Self-optimization of the guidance module of a rail-bound vehicle. In: Gausemeier, J., Rammig, F., Schäfer, W. (eds.) 7th International Heinz Nixdorf Symposium ‘Self-optimizing Mechatronic Systems: Design the Future’, February 20-21, pp. 85–100. HNI-Verlagsschriftenreihe, Paderborn (2008)

    Google Scholar 

  23. Harada, K., Sakuma, J., Kobayashi, S., Ono, I.: Uniform sampling of local Pareto-optimal solution curves by pareto path following and its applications in multi-objective GA. In: GECCO, pp. 813–820 (2007)

    Google Scholar 

  24. Henderson, M.E.: Multiple parameter continuation: Computing implicitly defined k-manifolds. International Journal of Bifurcation and Chaos 12, 451–476 (2002)

    Article  MATH  Google Scholar 

  25. Hestermeyer, T., Schlautmann, P., Ettingshausen, C.: Active suspension system for railway vehicles – system design and kinematics. In: 2nd IFAC - Conference on Mechatronic Systems, Berkeley, California, USA (2002)

    Google Scholar 

  26. Hillermeier, C.: Nonlinear Multiobjective Optimization - A Generalized Homotopy Approach. Birkhäuser (2001)

    Google Scholar 

  27. Horst, R., Tuy, H.: Global Optimization: Deterministic Approaches. Springer (1993)

    Google Scholar 

  28. Hsu, C.S.: Cell-to-cell mapping: a method of global analysis for nonlinear systems. Applied mathematical Sciences. Springer (1987)

    Google Scholar 

  29. Hsu, H.C.: Global analysis by cell mapping. International Journal of Bifurcation and Chaos 2, 727–771 (1992)

    Article  MATH  Google Scholar 

  30. Junge, O., Marsden, J.E., Ober-Blöbaum, S.: Optimal Reconfiguration of Formation Flying Spacecraft - a decentralized approach. In: IEEE Conference on Decision and Control, San Diego, CA, USA, pp. 5210–5215 (2006)

    Google Scholar 

  31. Karush, W.E.: Minima of functions of several variables with inequalities as side conditions. PhD thesis, University of Chicago (1939)

    Google Scholar 

  32. Klamroth, K., Tind, J., Wiecek, M.: Unbiased approximation in multicriteria optimization. Mathematical Methods of Operations Research 56, 413–437 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  33. Knoke, T., Romaus, C., Böcker, J., Dell’Aere, A., Witting, K.: Energy management for an onboard storage system based on multiobjective optimization. In: Proceedings of the IEEE 32nd Annual Conference on Industrial Electronics (IECON), pp. 4677–4682 (2006)

    Google Scholar 

  34. Krüger, M., Witting, K., Trächtler, A., Dellnitz, M.: Parametric model order reduction in hierarchical multiobjective optimization of mechatronic systems. In: 18th IFAC World Congress, Milano, Italy, August 28-September 2 (2010)

    Google Scholar 

  35. Kuhn, H., Tucker, A.: Nonlinear programming. In: Neumann, J. (ed.) Proceeding of the 2nd Berkeley Symposium on Mathematical Statistics and Probability (1951)

    Google Scholar 

  36. Leyendecker, S., Ober-Blöbaum, S., Marsden, J.E., Ortiz, M.: Discrete mechanics and optimal control for constrained systems. Optimal Control, Applications and Methods 31(6), 505–528 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  37. Li, R., Pottharst, A., Witting, K., Znamenshchykov, O., Böcker, J., Fröhleke, N., Feldmann, R., Dellnitz, M.: Design and implementation of a hybrid energy supply system for railway vehicles. In: Proc. of APEC2005, IEEE Applied Power Electronics Conference 2005, Austin, Texas, USA, pp. 474–480 (2005)

    Google Scholar 

  38. Logist, F., Houska, B., Diehl, M., Van Impe, J.: Fast pareto set generation for nonlinear optimal control problems with multiple objectives. Structural and Multidisciplinary Optimization 42, 591–603 (2010), doi:10.1007/s00158-010-0506-x

    Article  Google Scholar 

  39. Marsden, J.E., West, M.: Discrete mechanics and variational integrators. Acta Numerica 10, 357–514 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  40. Miettinen, K.: Nonlinear Multiobjective Optimization. Kluwer Academic Publishers, Boston (1999)

    MATH  Google Scholar 

  41. Milam, M., Mushambi, K., Murray, R.: A new computational approach to real-time trajectory generation for constrained mechanical systems. In: Proceedings of the 39th IEEE Conference on Decision and Control, vol. 1, pp. 845–551 (2000)

    Google Scholar 

  42. Moore, A., Ober-Blöbaum, S., Marsden, J.E.: Optimization of spacecraft trajectories: a method combining invariant manifold techniques and discrete mechanics and optimal. In: 19th AAS/AIAA Space Flight Mechanics Meeting, Februar 8-12 (2009)

    Google Scholar 

  43. Murray, R., Rathinam, M., Sluis, W.: Differential flatness of mechanical control systems: A catalog of prototype systems. In: Proceedings of the 1995 ASME International Congress and Exposition, San Francisco (1995)

    Google Scholar 

  44. Neue Bahntechnik Paderborn – Project. Web-Page, http://www.railcab.de

  45. Nocedal, J., Wright, S.: Numerical Optimization. Springer Series in Operations Research and Financial Engineering. Springer (2006)

    Google Scholar 

  46. Numerical Algorithms Group (C-Library). Web-Page, http://www.nag.co.uk/numeric/CL/CLdescription.asp

  47. Ober-Blöbaum, S.: Discrete mechanics and optimal control. PhD thesis. University of Paderborn (2008)

    Google Scholar 

  48. Ober-Blöbaum, S., Junge, O., Marsden, J.E.: Discrete mechanics and optimal control: an analysis. Control, Optimisation and Calculus of Variations 17(2), 322–352 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  49. Ober-Blöbaum, S., Timmermann, J.: Optimal control for a pitcher’s motion modeled as constrained mechanical system. In: 7th International Confenrence on Multibody Systems, Nonlinear Dynamics, and Control, ASME International Design Engineering Technical Conferences, San Diego, CA, USA (2009)

    Google Scholar 

  50. Petit, N., Milam, M., Murray, R.: Inversion based constrained trajectory optimization. In: 5th IFAC Symposium on Nonlinear Control Systems (2001)

    Google Scholar 

  51. Pottharst, A., Baptist, K., Schütze, O., Böcker, J., Fröhlecke, N., Dellnitz, M.: Operating point assignment of a linear motor driven vehicle using multiobjective optimization methods. In: Proceedings of the 11th International Conference EPE-PEMC 2004, Riga, Latvia (2004)

    Google Scholar 

  52. Recchioni, M.C.: A path following method for box-constrained multiobjective optimization with applications to goal programming problems. Mathematical Methods of Operations Research 58, 69–85 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  53. Rheinboldt, W.: On the computation of multi-dimensional solution manifolds of parametrized equations. Numerische Mathematik 53, 165–181 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  54. Ringkamp, M., Ober-Blöbaum, S., Dellnitz, M., Schütze, O.: Handling high dimensional problems with multi-objective continuation methods via successive approximation of the tangent space. To appear in Engineering Optimization (2011)

    Google Scholar 

  55. Schäffler, S., Schultz, R., Weinzierl, K.: A stochastic method for the solution of unconstrained vector optimization problems. Journal of Optimization Theory and Applications 114(1), 209–222 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  56. Schneider, T., Schulz, B., Henke, C., Witting, K., Steenken, D., Böcker, J.: Energy transfer via linear doubly-fed motor in different operating modes. In: Proceedings of the International Electric Machines and Drives Conference, Miami, Florida, USA, May 3-6 (2009)

    Google Scholar 

  57. Schütze, O.: Set Oriented Methods for Global Optimization. PhD thesis, University of Paderborn (2004), http://ubdata.uni-paderborn.de/ediss/17/2004/schuetze/

  58. Schütze, O., Dell’Aere, A., Dellnitz, M.: On continuation methods for the numerical treatment of multi-objective optimization problems. In: Branke, J., Deb, K., Miettinen, K., Steuer, R.E. (eds.) Practical Approaches to Multi-Objective Optimization. Dagstuhl Seminar Proceedings, vol. 04461. Internationales Begegnungs- und Forschungszentrum (IBFI), Schloss Dagstuhl (2005), http://drops.dagstuhl.de/opus/volltexte/2005/349

    Google Scholar 

  59. Schütze, O., Jourdan, L., Legrand, T., Talbi, E.-G., Wojkiewicz, J.L.: New analysis of the optimization of electromagnetic shielding properties using conducting polymers and a multi-objective approach. Polymers for Advanced Technologies 19, 762–769 (2008)

    Article  Google Scholar 

  60. Schütze, O., Vasile, M., Junge, O., Dellnitz, M., Izzo, D.: Designing optimal low thrust gravity assist trajectories using space pruning and a multi-objective approach. Engineering Optimization 41(2), 155–181 (2009)

    Article  MathSciNet  Google Scholar 

  61. Van Nieuwstadt, M.J., Murray, R.M.: Real-time trajectory generation for differentially flat systems. International Journal of Robust and Nonlinear Control 8(11), 995–1020 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  62. Witting, K., Schulz, B., Dellnitz, M., Böcker, J., Fröhleke, N.: A new approach for online multiobjective optimization of mechatronic systems. International Journal on Software Tools for Technology Transfer STTT 10(3), 223–231 (2008)

    Article  Google Scholar 

  63. Zhang, W., Inanc, T., Ober-Blöbaum, S., Marsden, J.E.: Optimal trajectory generation for a dynamic glider in ocean flows modeled by 3D B-Spline functions. In: IEEE International Conference on Robotics and Automation (ICRA), Pasadena, CA, USA (2008)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computer Science Department, CINVESTAV-IPN, Av. IPN 2508, C. P. 07360, Col. San Pedro Zacatenco, Mexico City, Mexico

    Oliver Schütze

  2. Chair of Applied Mathematics, University of Paderborn, Warburger Str. 100, D-33098, Paderborn, Germany

    Katrin Witting, Sina Ober-Blöbaum & Michael Dellnitz

Authors
  1. Oliver Schütze
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Katrin Witting
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sina Ober-Blöbaum
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Michael Dellnitz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Oliver Schütze .

Editor information

Editors and Affiliations

  1. Computer Science and Communications, Research Unit, University of Luxembourg, rue Richard Coudenhove-Kalergi 6, Luxembourg, L-1359, Luxembourg

    Emilia Tantar

  2. , Computer Science and Communications, University of Luxembourg, rue Richard Coudenhove-Kalergi 6, Luxembourg, 1359, Luxembourg

    Alexandru-Adrian Tantar

  3. Computer Science, and Communications, University of Luxembourg, rue Richard Coudenhove-Kalergi 6, Luxembourg, L-1359, Luxembourg

    Pascal Bouvry

  4. Bordeaux Mathematical Institute, INRIA Bordeaux-Sud Ouest, Université Bordeaux I, cours de la Libération 351, Talence Cedex, 33405, France

    Pierre Del Moral

  5. Bâtiment Leyteire, UFR Sciences et Modélisation, Université Bordeaux II, 3ter place de la Victoire, Bordeaux, 33000, France

    Pierrick Legrand

  6. , Computer Science Department, CINVESTAV-IPN, Col. San Pedro Zacatenco 2508, Mexico City, 07360, Mexico

    Carlos A. Coello Coello

  7. , Computer Science Department, CINVESTAV-IPN, Col. San Pedro Zacatenco 2508, Mexico City, 07360, Mexico

    Oliver Schütze

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer Berlin Heidelberg

About this chapter

Cite this chapter

Schütze, O., Witting, K., Ober-Blöbaum, S., Dellnitz, M. (2013). Set Oriented Methods for the Numerical Treatment of Multiobjective Optimization Problems. In: Tantar, E., et al. EVOLVE- A Bridge between Probability, Set Oriented Numerics and Evolutionary Computation. Studies in Computational Intelligence, vol 447. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-32726-1_5

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-32726-1_5

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-32725-4

  • Online ISBN: 978-3-642-32726-1

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics