Abstract
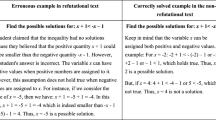
Erroneous examples are an instructional technique that hold promise to help children learn. In the study reported in this paper, sixth and seventh grade math students were presented with erroneous examples of decimal problems and were asked to explain and correct those examples. The problems were presented as interactive exercises on the Internet, with feedback provided on correctness of the student explanations and corrections. A second (control) group of students were given problems to solve, also with feedback on correctness. With over 100 students per condition, an erroneous example effect was found: students who worked with the interactive erroneous examples did significantly better than the problem solving students on a delayed posttest. While this finding is highly encouraging, our ultimate research question is this: how can erroneous examples be adaptively presented to students, targeted at their most deeply held misconceptions, to best leverage their effectiveness? This paper discusses how the results of the present study will lead us to an adaptive version of the erroneous examples material.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Tsamir, P., Tirosh, D.: In-service mathematics teachers’ views of errors in the classroom. In: International Symposium: Elementary Mathematics Teaching, Prague (2003)
Skinner, B.F.: The behavior of organisms: An experimental analysis. Appleton-Century, New York (1938)
Borasi, R.: Reconceiving Mathematics Instruction: A Focus on Errors. Ablex Publishing Corporation (1996)
Catrambone, R.: The subgoal learning model: Creating better examples so that students can solve novel problems. Journal of Experimental Psychology: General 1998 127(4), 355–376 (1998)
McLaren, B.M., Lim, S., Koedinger, K.R.: When and how often should worked examples be given to students? New results and a summary of the current state of research. In: Proceedings of the 30th Annual Conference of the Cognitive Science Society, pp. 2176–2181. Cog. Sci. Society, Austin (2008)
Renkl, A., Atkinson, R.K.: Learning from worked-out examples and problem solving. In: Plass, J.L., Moreno, R., Brünken, R. (eds.) Cognitive Load Theory. Cambridge University Press, Cambridge (2010)
Sweller, J., Cooper, G.A.: The use of worked examples as a substitute for problem solving in learning algebra. Cognition and Instruction 2, 59–89 (1985)
Zhu, X., Simon, H.A.: Learning mathematics from examples and by doing. Cognition and Instruction 4(3), 137–166 (1987)
Roy, M., Chi, M.T.H.: The self-explanation principle in multimedia learning. In: Mayer, R.E. (ed.) The Cambridge Handbook of Multimedia Learning, pp. 271–286. Cambridge University Press, New York (2005)
Sweller, J., Van Merriënboer, J.J.G., Paas, F.G.W.C.: Cognitive architecture and instructional design. Educational Psychology Review 10, 251–296 (1998)
Leelawong, K., Biswas, G.: Designing learning by teaching agents: The Betty’s Brain system. Int’l Journal of Artificial Intelligence in Education 18(3), 181–208 (2008)
Siegler, R.S.: How does change occur: A microgenetic study of number conservation. Cognitive Psychology 28, 225–273 (1995)
Grosse, C.S., Renkl, A.: Finding and fixing errors in worked examples: Can this foster learning outcomes? Learning and Instruction 17(6), 612–634 (2007)
Tsovaltzi, D., Melis, E., McLaren, B.M., Meyer, A.-K., Dietrich, M., Goguadze, G.: Learning from Erroneous Examples: When and How Do Students Benefit from Them? In: Wolpers, M., Kirschner, P.A., Scheffel, M., Lindstaedt, S., Dimitrova, V. (eds.) EC-TEL 2010. LNCS, vol. 6383, pp. 357–373. Springer, Heidelberg (2010)
Isotani, S., Adams, D., Mayer, R.E., Durkin, K., Rittle-Johnson, B., McLaren, B.M.: Can Erroneous Examples Help Middle-School Students Learn Decimals? In: Kloos, C.D., Gillet, D., Crespo García, R.M., Wild, F., Wolpers, M. (eds.) EC-TEL 2011. LNCS, vol. 6964, pp. 181–195. Springer, Heidelberg (2011)
Irwin, K.C.: Using everyday knowledge of decimals to enhance understanding. Journal for Research in Mathematics Education 32(4), 399–420 (2001)
Resnick, L.B., Nesher, P., Leonard, F., Magone, M., Omanson, S., Peled, I.: Conceptual bases of arithmetic errors: The case of decimal fractions. Journal for Research in Mathematics Education 20(1), 8–27 (1989)
Sackur-Grisvard, C., Léonard, F.: Intermediate cognitive organizations in the process of learning a mathematical concept: The order of positive decimal numbers. Cognition and Instruction 2, 157–174 (1985)
Putt, I.J.: Preservice teachers ordering of decimal numbers: When more is smaller and less is larger! Focus on Learning Problems in Mathematics 17(3), 1–15 (1995)
Stacey, K., Helme, S., Steinle, V., Baturo, A., Irwin, K., Bana, J.: Preservice teachers’ knowledge of difficulties in decimal numeration. Journal of Mathematics Teacher Education 4, 205–225 (2001)
Aleven, V., McLaren, B.M., Sewall, J., Koedinger, K.R.: A new paradigm for intelligent tutoring systems: Example-tracing tutors. International Journal of Artificial Intelligence in Education 19(2), 105–154 (2009)
Schmidt, R.A., Bjork, R.A.: New conceptualizations of practice: Common principles in three paradigms suggest new concepts for training. Psych. Sci. 3(4), 207–217 (1992)
Goguadze, G., Sosnovsky, S., Isotani, S., McLaren, B.M.: Evaluating a bayesian student model of decimal misconceptions. In: Proceedings of the 4th International Conference on Educational Data Mining (EDM 2011), pp. 301–306 (2011)
Stacey, K., Sonenberg, E., Nicholson, A., Boneh, T., Steinle, V.: A Teacher Model Exploiting Cognitive Conflict Driven by a Bayesian Network. In: Brusilovsky, P., Corbett, A.T., de Rosis, F. (eds.) UM 2003. LNCS, vol. 2702, pp. 352–362. Springer, Heidelberg (2003)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
McLaren, B.M. et al. (2012). To Err Is Human, to Explain and Correct Is Divine: A Study of Interactive Erroneous Examples with Middle School Math Students. In: Ravenscroft, A., Lindstaedt, S., Kloos, C.D., Hernández-Leo, D. (eds) 21st Century Learning for 21st Century Skills. EC-TEL 2012. Lecture Notes in Computer Science, vol 7563. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-33263-0_18
Download citation
DOI: https://doi.org/10.1007/978-3-642-33263-0_18
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-33262-3
Online ISBN: 978-3-642-33263-0
eBook Packages: Computer ScienceComputer Science (R0)