Skip to main content
Springer Nature Link
Log in

Monotone Multigrid Methods Based on Parametric Finite Elements

  • Conference paper
  • First Online:
Domain Decomposition Methods in Science and Engineering XX

Part of the book series: Lecture Notes in Computational Science and Engineering ((LNCSE,volume 91))

  • 2119 Accesses

Summary

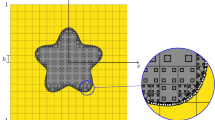
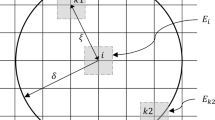
In this paper, a particular technique for the application of elementary multilevel ideas to problems with warped boundaries is studied in the context of the numerical simulation of elastic contact problems. Combining a general multilevel setting with a different perspective, namely an advanced geometric modeling point of view, we present a (monotone) multigrid method based on a hierarchy of parametric finite element spaces. For the construction, a full-dimensional parameterization of high order is employed which accurately represents the computational domain.The purpose of the volume parametric finite element discretization put forward here is two-fold. On the one hand, it allows for an elegant multilevel hierarchy to be used in preconditioners. On the other hand, it comes with particular advantages for the modeling of contact problems. After all, the long-term objective lies in an increased flexibility of h p-adaptive methods for contact problems.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

Bibliography

  1. S. Bartels, C. Carstensen, and A. Hecht. P2Q2Iso2D = 2D isoparametric FEM in Matlab. J. Comput. Appl. Math., 192(2):219–250, 2006.

    Article  MathSciNet  MATH  Google Scholar 

  2. A. Chernov, M. Maischak, and E.P. Stephan. A priori estimates for h p penalty BEM for contact problems in elasticity. Comput. Methods Appl. Mech. Engrg., 196(37–40):3871–3880, 2007.

    Article  MathSciNet  MATH  Google Scholar 

  3. P.G. Ciarlet. The Finite Element Method for Elliptic Problems. North-Holland, Amsterdam, 1978.

    MATH  Google Scholar 

  4. W. Dahmen, C.A. Micchelli, and H.P. Seidel. Blossoming begets B-spline bases built better by B-patches. Math. Comput., 59(199):97–115, 1992.

    MathSciNet  MATH  Google Scholar 

  5. T. Dickopf. Multilevel Methods Based on Non-Nested Meshes. PhD thesis, University of Bonn, 2010. http://hss.ulb.uni-bonn.de/2010/2365.

  6. T. Dickopf and R. Krause. Efficient simulation of multi-body contact problems on complex geometries: a flexible decomposition approach using constrained minimization. Int. J. Numer. Methods Engrg., 77(13):1834–1862, 2009.

    Article  MathSciNet  MATH  Google Scholar 

  7. B. Flemisch and B. Wohlmuth. Stable Lagrange multipliers for quadrilateral meshes of curved interfaces in 3d. Comput. Methods Appl. Mech. Engrg., 196(8):1589–1602, 2007.

    Article  MathSciNet  MATH  Google Scholar 

  8. W.J. Gordon and C.A. Hall. Transfinite element methods: blending-function interpolation over arbitrary curved element domains. Numer. Math., 21(2):109–129, 1973.

    Article  MathSciNet  MATH  Google Scholar 

  9. H. Harbrecht. A finite element method for elliptic problems with stochastic input data. Appl. Numer. Math., 60(3):227–244, 2010.

    Article  MathSciNet  MATH  Google Scholar 

  10. H. Harbrecht and M. Randrianarivony. From computer aided design to wavelet BEM. Comput. Visual. Sci., 13(2):69–82, 2010.

    Article  MathSciNet  MATH  Google Scholar 

  11. T.J.R. Hughes, J.A. Cottrell, and Y. Bazilevs. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Engrg., 194(39–41):4135–4195, 2005.

    Article  MathSciNet  MATH  Google Scholar 

  12. R. Kornhuber. Adaptive Monotone Multigrid Methods for Nonlinear Variational Problems. Teubner, Stuttgart, 1997.

    MATH  Google Scholar 

  13. R. Krause. On the multiscale solution of constrained minimization problems. In U. Langer et al., editor, Domain Decomposition Methods in Science and Engineering XVII, volume 60 of Lect. Notes Comput. Sci. Eng., pages 93–104. Springer, 2008.

    Google Scholar 

  14. X.J. Luo, M.S. Shephard, J.F. Remacle, R.M. O’Bara, M.W. Beall, B. Szabó, and R. Actis. p-version mesh generation issues. In Proceedings of the 11th International Meshing Roundtable, pages 343–354. 2002.

    Google Scholar 

  15. M. Randrianarivony. Tetrahedral transfinite interpolation with B-patch faces: construction and regularity. INS Preprint No. 0803. University of Bonn, 2008.

    Google Scholar 

  16. P. Seshaiyer and M. Suri. Uniform h p convergence results for the mortar finite element method. Math. Comput., 69(230):521–546, 2000.

    MathSciNet  MATH  Google Scholar 

  17. M. Zlámal. The finite element method in domains with curved boundaries. Int. J. Numer. Methods Engrg., 5(3):367–373, 1973.

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Helmut Harbrecht and Maharavo Randrianarivony for bringing this topic to their attention. Moreover, we acknowledge the latter for providing his code for the tetrahedral transfinite interpolation described in [15]. The valuable assistance of Lukas Döring in the implementation of a flexible interface of the parameterization concept to our finite element code is appreciated. This work was supported by the Bonn International Graduate School in Mathematics and the Ford University Research Program.

Author information

Authors and Affiliations

  1. Institute of Computational Science, University of Lugano, Via G. Buffi 13, 6904, Lugano, Switzerland

    Thomas Dickopf & Rolf Krause

Authors
  1. Thomas Dickopf
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rolf Krause
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thomas Dickopf .

Editor information

Editors and Affiliations

  1. , Department of Mathematics, University of California, San Diego, Gilman Drive 9500, La Jolla, 92093-0112, California, USA

    Randolph Bank

  2. , Department of Mathematics, University of California, San Diego, Gilman Drive 9500, La Jolla, 92093-0112, California, USA

    Michael Holst

  3. , Courant Institute of Mathematical, New York University, Mercer Street 251, New York, 10012-1185, New York, USA

    Olof Widlund

  4. , Department of Mathematics, Pennsylvania State University, State College, 16802, Pennsylvania, USA

    Jinchao Xu

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Dickopf, T., Krause, R. (2013). Monotone Multigrid Methods Based on Parametric Finite Elements. In: Bank, R., Holst, M., Widlund, O., Xu, J. (eds) Domain Decomposition Methods in Science and Engineering XX. Lecture Notes in Computational Science and Engineering, vol 91. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-35275-1_37

Download citation

Publish with us

Policies and ethics