Abstract
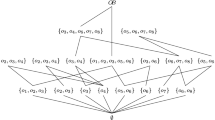
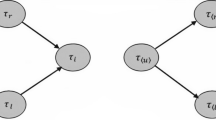
Knowledge (information) granulation is one of the fundamental concepts of information processing leading to a new discipline called granular computing. One of the basic problems addressed by granular computing is the higher order granulation: how to collect basic information granules into a new granule. In the paper we address this problem by purely mathematical means using two well-established methodologies of information processing: near set theory and rough set theory. We start with the simple fact that the theory of near sets and the theory of rough sets share a common metric root. Since a probe function and an equivalence relation can be regarded as a pseudometric on U, in actual fact the underlying structure of both theories is a family of pseudometrics. The same starting point one can find in metric topology: an arbitrary family of pseudometrics is called a pregauge structure and when this family additionally separates all points, it is called a gauge structure. Pregauge structures characterise all completely regular spaces, whereas gauge structures correspond to all Hausdorff completely regular spaces (often called gauge spaces). In consequence, a perceptual system and an information system can be regarded as both pregauge structures and as topological completely regular spaces. A perceptual system or an approximation space does usually not separate all points and thus does not form a gauge space. Therefore in the paper we introduce the concept of a separating completion of a pregauge structure. This notion allows us to build a non-trivial topology on the set of perceptual elementary granules of a perceptual system (or an information system); in other words, a separating completion induces the higher order granulation. The completion requirement induces also a topology on a set of objects, which is locally homeomorphic to the the topology on basic information granules. Apart from topological results, we shall also discuss both topologies using category theory. A perceptual system may be actually enriched to an abelian group or a vector space, while unchanging the original granulation. It also gives rise to a quite rich sheaf of all real-valued functions preserving the basic granulation. Summing up, our aim is to build rich mathematical structures which do not change basic granulation and may be used to solve the problem of higher order granules.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Blute, R., Scott, P.: Category Theory for Linear Logicians. In: Ehrhard, T., Jirard, J., Ruet, P., Scott, P. (eds.) Linear Logic in Computer Science, pp. 3–64. Cambridge University Press (2005)
Cattaneo, G., Ciucci, D.: A Quantitative Analysis of Preclusivity vs. Similarity Based Rough Approximations. In: Alpigini, J.J., Peters, J.F., Skowron, A., Zhong, N. (eds.) RSCTC 2002. LNCS (LNAI), vol. 2475, pp. 69–76. Springer, Heidelberg (2002)
Dugundji, J.: Topology. Allyn and Bacon, Boston (1966)
Engelking, R.: General Topology. Heldermann Verlag (1989)
Gomolińska, A.: Approximation Spaces Based on Relations of Similarity and Dissimilarity of Objects. Fundamenta Informaticae 79, 319–333 (2007)
Mac Lane, S., Moerdijk, I.: Sheaves in Geometry and Logic: A First Introduction to Topos Theory. Springer (1992)
Marek, W., Pawlak, Z.: Information storage and retrieval systems, mathematical foundations. Theoretical Computer Science 1(4), 331–354 (1976)
Pawlak, Z.: Information systems – Theoretical Foundations. International Journal of Computer and Information Sciences 11, 341–356 (1981)
Pawlak, Z.: Rough sets. Int. J. Computer and Information Sci. 11, 341–356 (1982)
Pawlak, Z.: Rough Sets: Theoretical Aspects of Reasoning About Data. Kluwer, Dordrecht (1991)
Pedrycz, W., Skowron, A., Kreinovich, V. (eds.): The Handbook of Granular Computing. Wiley (2008)
Peters, J.F.: Near Sets. Special Theory About Nearness of Objects. Fundamenta Informaticae 75, 407–433 (2007)
Peters, J.F., Skowron, A., Stepaniuk, J.: Nearness of Objects: Extension of Approximation Space Model. Fundamenta Informaticae 79, 497–512 (2007)
Peters, J.F., Wasilewski, P.: Foundations of Near Sets. Information Sciences 179, 3091–3109 (2009)
Rasiowa, H.: Algebraic Models of Logics. Warsaw University Press, Warsaw (2001)
Willard, S.: General Topology. Addison-Wesley Publishing Company (1970)
Wiweger, A.: On topological rough sets. Bulletin of the Polish Academy of Sciences, Mathematics 37, 89–93 (1989)
Wolski, M.: Gauges, Pregauges and Completions: Some Theoretical Aspects of Near and Rough Set Approaches to Data. In: Yao, J., Ramanna, S., Wang, G., Suraj, Z. (eds.) RSKT 2011. LNCS, vol. 6954, pp. 559–568. Springer, Heidelberg (2011)
Zimmermann, H.J.: Fuzzy Set Theory - and its Applications. Springer (2001)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Wolski, M. (2013). Granular Computing: Topological and Categorical Aspects of Near and Rough Set Approaches to Granulation of Knowledge. In: Peters, J.F., Skowron, A., Ramanna, S., Suraj, Z., Wang, X. (eds) Transactions on Rough Sets XVI. Lecture Notes in Computer Science, vol 7736. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-36505-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-642-36505-8_3
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-36504-1
Online ISBN: 978-3-642-36505-8
eBook Packages: Computer ScienceComputer Science (R0)