Abstract
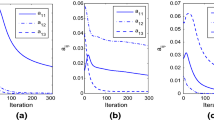
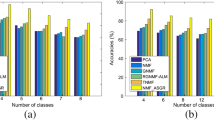
It is known that the sparseness of the factor matrices by Nonnegative Matrix Factorization can influence the clustering performance. In order to improve the ability of the sparse representations of the NMF, we proposed the new algorithm for Nonnegatie Matrix Factorization, coined nonnegative matrix factorization on orthogonal subspace with smoothed L0 norm constrained, in which the generation of orthogonal factor matrices with smoothed L0 norm constrained are the parts of objective function minimization. Also we develop simple multiplicative updates for our proposed method. Experiment on three real-world databases (Iris, UCI, ORL) show that our proposed method can achieve the best or close to the best in clustering and in the way of the sparse representation than other methods.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
References
Lee, D.D., et al.: Algorithms for non-negative matrix factorization. In: Advances in Neural Information Processing (Proc. NIPS), vol. 13, pp. 556–562 (2000)
Li, S., Hou, X., Zhang, H., Cheng, Q.: Learning spatially localized, parts-based representation. In: IEEE Comput. Soc. Conf. Comput. Vision Pattern Recognition, vol. 1, pp. 207–212 (2001)
Hoyer, P.O.: Nonnegative Matrix Factorization with Sparseness Constraints. J. Machine Learning Research 5, 1457–1469 (2004)
Yang, Z., Laaksonen, J.: Multiplicative updates for non-negative projections. Neurocomputing 71(1-3), 363–373 (2007)
Ding, C., Li, T., Peng, W., Park, H.: Orthogonal nonnegative matrix trifactorizations for clustering. In: KDD 2006: Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 126–135. ACM, New York (2006)
Li, Z., Wu, X., Peng, H.: Nonnegative Matrix Factorization on Orthogonal Subspace. Pattern Recognition Letters 31, 905–911 (2010)
Donoho, D.L., Elad, M., Temlyakov, V.: Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans. Info. Theory 52(1), 6–18 (2006)
Yang, Z., Chen, X., Zhou, G., Xie, S.: Spectral unmixing using nonnegative matrix factorization with smoothed L0 norm constraint. In: Proceedings of SPIE, vol. 7494 (2009)
Hosen Mohimani, G., Babaie-Zadeh, M., Jutten, C.: A fast approach for overcomplete sparse decomposition based on smoothed l0 norm. IEEE Transactions on Signal Processing 57(1), 289–301 (2009)
Zdunek, R., Cichocki, A.: Nonnegative matrix factorization with constrained second order optimization. Signal Processing 87, 1904–1916 (2007)
Yang, Z., Oja, E.: Linear and Nonlinear Projective Nonnegative Matrix Factorization. IEEE Trans. Neural. Networks 21(5), 734–747 (2010)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Ye, J., Jin, Z. (2013). Nonnegative Matrix Factorization on Orthogonal Subspace with Smoothed L0 Norm Constrained. In: Yang, J., Fang, F., Sun, C. (eds) Intelligent Science and Intelligent Data Engineering. IScIDE 2012. Lecture Notes in Computer Science, vol 7751. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-36669-7_1
Download citation
DOI: https://doi.org/10.1007/978-3-642-36669-7_1
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-36668-0
Online ISBN: 978-3-642-36669-7
eBook Packages: Computer ScienceComputer Science (R0)