Online Checkpointing with Improved Worst-Case Guarantees

Abstract

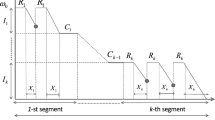
In the online checkpointing problem, the task is to continuously maintain a set of k checkpoints that allow to rewind an ongoing computation faster than by a full restart. The only operation allowed is to replace an old checkpoint by the current state. Our aim are checkpoint placement strategies that minimize rewinding cost, i.e., such that at all times T when requested to rewind to some time t ≤ T the number of computation steps that need to be redone to get to t from a checkpoint before t is as small as possible. In particular, we want that the closest checkpoint earlier than t is not further away from t than q _k times the ideal distance T / (k + 1), where q _k is a small constant.

Improving over earlier work showing 1 + 1/k ≤ q _k  ≤ 2, we show that q _k can be chosen asymptotically less than 2. We present algorithms with asymptotic discrepancy q _k  ≤ 1.59 + o(1) valid for all k and q _k  ≤ ln (4) + o(1) ≤ 1.39 + o(1) valid for k being a power of two. Experiments indicate the uniform bound p _k  ≤ 1.7 for all k. For small k, we show how to use a linear programming approach to compute good checkpointing algorithms. This gives discrepancies of less than 1.55 for all k < 60.

We prove the first lower bound that is asymptotically more than one, namely q _k  ≥ 1.30 − o(1). We also show that optimal algorithms (yielding the infimum discrepancy) exist for all k.