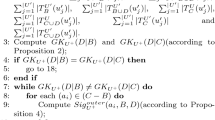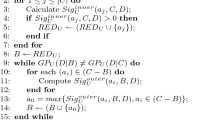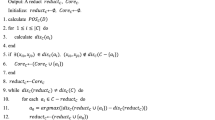Abstract
This paper proposes an incremental attribute selection method based on rough sets from partially uncertain and incremental or large decision system. The uncertainty exists only in the decision attributes (classes) and is represented by the belief function theory. The simplification of large or incremental uncertain decision table is based on computing possible reducts by the means of belief discernibility matrix and function under the belief function framework from two or more sub-decision tables.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bosse, E., Jousseleme, A.L., Grenier, D.: A new distance between two bodies of evidence. Information Fusion 2, 91–101 (2001)
Deng, D., Huang, H.: A New Discernibility Matrix and Function, Rough Sets and Knowledge Technology, pp. 114–121. Springer (2006)
Pawlak, Z.: Rough Sets. International Journal of Computer and Information Sciences 11, 341–356 (1982)
Pawlak, Z., Zdzislaw, A.: Rough Sets: Theoretical Aspects of Reasoning About Data, 7th edn. Kluwer Academic Publishing, Dordrecht (1991) ISBN 0-7923-1472-7
Pawlak, Z., Rauszer, C.M.: Dependency of attributes in Information systems. Bull. Polish Acad. Sci., Math. 33, 551–559 (1985)
Rauszer, C.M.: Reducts in Information systems. Fundamenta Informaticae (1990)
Shafer, G.: A mathematical theory of evidence. Princeton University Press, Princeton (1976)
Skowron, A., Rauszer, C.: The Discernibility Matrices and Functions in Information Systems. In: Slowiski, R. (ed.) Intelligent Decision Support, Handbook of Applications and Advances of the Rough Set Theory, pp. 311–362. Kluwer Academic Publishers, Dordrecht (1992)
Skowron, A.: Rough Sets in KDD. Special Invited Speaking. In: WCC 2000 in Beijing (August 2000)
Smets, P., Kennes, R.: The transferable belief model. Artificial Intelligence 66, 191–236 (1994)
Smets, P.: The transferable belief model for quantified belief representation. In: Gabbay, D.M., Smets, P. (eds.) Handbook of Defeasible Reasoning and Uncertainty Management Systems, vol. 1, pp. 207–301. Kluwer, Doordrecht (1998)
Skowron, A., Grzymala-Busse, J.W.: From rough set theory to evidence theory. In: Advances in the Dempster-Shafer Theory of Evidence, New York, pp. 193–236 (1994)
Trabelsi, S., Elouedi, Z., Lingras, P.: Heuristic for Attribute Selection Using Belief Discernibility Matrix. In: Li, T., Nguyen, H.S., Wang, G., Grzymala-Busse, J., Janicki, R., Hassanien, A.E., Yu, H. (eds.) RSKT 2012. LNCS, vol. 7414, pp. 129–138. Springer, Heidelberg (2012)
Trabelsi, S., Elouedi, Z., Lingras, P.: Exhaustive search with belief discernibility matrix and function. In: Zaïane, O.R., Zilles, S. (eds.) Canadian AI 2013. LNCS, vol. 7884, pp. 162–173. Springer, Heidelberg (2013)
Trabelsi, S., Elouedi, Z., Lingras, P.: Belief rough set classifier. In: Gao, Y., Japkowicz, N. (eds.) AI 2009. LNCS, vol. 5549, pp. 257–261. Springer, Heidelberg (2009)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Trabelsi, S., Elouedi, Z., Lingras, P. (2013). Belief Discernibility Matrix and Function for Incremental or Large Data. In: Ciucci, D., Inuiguchi, M., Yao, Y., Ślęzak, D., Wang, G. (eds) Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. RSFDGrC 2013. Lecture Notes in Computer Science(), vol 8170. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-41218-9_8
Download citation
DOI: https://doi.org/10.1007/978-3-642-41218-9_8
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-41217-2
Online ISBN: 978-3-642-41218-9
eBook Packages: Computer ScienceComputer Science (R0)