Skip to main content
SpringerLink
Log in

Comparison of Two Numerical Approaches to Boussinesq Paradigm Equation

  • Conference paper
Numerical Analysis and Its Applications (NAA 2012)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 8236))

Included in the following conference series:

Abstract

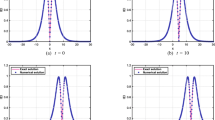
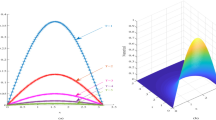
In order to study the time behavior and structural stability of the solutions of Boussinesq Paradigm Equation, two different numerical approaches are designed. The first one (A1) is based on splitting the fourth order equation to a system of a hyperbolic and an elliptic equation. The corresponding implicit difference scheme is solved with an iterative solver. The second approach (A2) consists in devising of a finite difference factorization scheme. This scheme is split into a sequence of three simpler ones that lead to five-diagonal systems of linear algebraic equations. The schemes, corresponding to both approaches A1 and A2, have second order truncation error in space and time. The results obtained by both approaches are in good agreement with each other.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 39.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

References

  1. Christov, C.I.: An Energy-consistent Dispersive Shallow-water Model. Wave Motion 34, 161–174 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  2. Boussinesq, J.V.: Théorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. Journal de Mathématiques Pures et Appliquées 17, 55–108 (1872)

    MATH  Google Scholar 

  3. Christov, C.I., Choudhury, J.: Perturbation Solution for the 2D Boussinesq Equation. Mech. Res. Commun. 38, 274–281 (2011)

    Article  MATH  Google Scholar 

  4. Christov, C.I., Todorov, M.T., Christou, M.A.: Perturbation Solution for the 2D Shallow-water Waves. In: AIP Conference Proceedings, vol. 1404, pp. 49–56 (2011)

    Google Scholar 

  5. Christov, C.I.: Numerical Implementation of the Asymptotic Boundary Conditions for Steadily Propagating 2D Solitons of Boussinesq Type Equations. Math. Comp. Simulat. 82, 1079–1092 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  6. Christou, M.A., Christov, C.I.: Fourier-Galerkin Method for 2D Solitons of Boussinesq Equation. Math. Comput. Simul. 74, 82–92 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chertock, A., Christov, C.I., Kurganov, A.: Central-Upwind Schemes for the Boussinesq Paradigm Equation. Computational Science and High Performance Computing IV, NNFM 113, 267–281 (2011)

    Article  MathSciNet  Google Scholar 

  8. Christov, C.I., Kolkovska, N., Vasileva, D.: On the Numerical Simulation of Unsteady Solutions for the 2D Boussinesq Paradigm Equation. In: Dimov, I., Dimova, S., Kolkovska, N. (eds.) NMA 2010. LNCS, vol. 6046, pp. 386–394. Springer, Heidelberg (2011)

    Chapter  Google Scholar 

  9. Christov, C.I., Kolkovska, N., Vasileva, D.: Numerical Investigation of Unsteady Solutions for the 2D Boussinesq Paradigm Equation. 5th Annual Meeting of the Bulgarian Section of SIAM. In: BGSIAM 2010 Proceedings, pp. 11–16 (2011)

    Google Scholar 

  10. Ames, W.F.: Nonlinear Partial Differential Equations in Engineering. Academic Press (1965)

    Google Scholar 

  11. Christov, C.I., Velarde, M.G.: Inelastic interaction of Boussinesq solitons. J. Bifurcation & Chaos 4, 1095–1112 (1994)

    Article  MATH  Google Scholar 

  12. Kolkovska, N.: Convergence of Finite Difference Schemes for a Multidimensional Boussinesq Equation. In: Dimov, I., Dimova, S., Kolkovska, N. (eds.) NMA 2010. LNCS, vol. 6046, pp. 469–476. Springer, Heidelberg (2011)

    Chapter  Google Scholar 

  13. Dimova, M., Kolkovska, N.: Comparison of Some Finite Difference Schemes for Boussinesq Paradigm Equation. In: Adam, G., Buša, J., Hnatič, M. (eds.) MMCP 2011. LNCS, vol. 7125, pp. 215–220. Springer, Heidelberg (2012)

    Chapter  Google Scholar 

  14. Kolkovska, N., Dimova, M.: A New Conservative Finite Difference Scheme for Boussinesq Paradigm Equation. Cent. Eur. J. Math. 10(3), 1159–1171 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Kolkovska, N.: Two Families of Finite Difference Schemes for Multidimensional Boussinesq Equation. In: AIP Conference Series, vol. 1301, pp. 395–403 (2010)

    Google Scholar 

  16. van der Vorst, H.: Iterative Krylov Methods for Large Linear Systems. Cambridge Monographs on Appl. and Comp. Math. 13 (2009)

    Google Scholar 

  17. Samarskii, A.: The Theory of Difference Schemes. Marcel Dekker Inc. (2001)

    Google Scholar 

  18. Samarskii, A.A., Nikolaev, E.: Numerical Methods for Grid Equations. Birkhäuser Verlag (1989)

    Google Scholar 

  19. Christov, C.I.: Gaussian Elimination with Pivoting for Multidiagonal Systems. Internal Report, University of Reading 4 (1994)

    Google Scholar 

  20. Samarskii, A.A., Vabishchevich, P.N.: Numerical Methods for Solving Inverse Problems of Mathematical Physics. Walter de Gruyter (2007)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics and Informatics, Bulgarian Acad. Sci., Acad. G. Bonchev str., bl.8, 1113, Sofia, Bulgaria

    Milena Dimova & Daniela Vasileva

Authors
  1. Milena Dimova
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Daniela Vasileva
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Institute of Information and Communication Technlogies, Bulgarian Academy of Sciences, Acad. G. Bonchev, Bl25A, 1113, Sofia, Bulgaria

    Ivan Dimov

  2. Department of Applied Analysis, Pázm\’{a}ny P\’{e}ter s\’{e}t\’{a}ny 1/C,, Eötvös Loránd University, 1117, Budapest, Hungary

    István Faragó

  3. University of Rousse, 8 Studentska Str.,, 7017, Rousse, Bulgaria

    Lubin Vulkov

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Dimova, M., Vasileva, D. (2013). Comparison of Two Numerical Approaches to Boussinesq Paradigm Equation. In: Dimov, I., Faragó, I., Vulkov, L. (eds) Numerical Analysis and Its Applications. NAA 2012. Lecture Notes in Computer Science, vol 8236. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-41515-9_27

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-41515-9_27

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-41514-2

  • Online ISBN: 978-3-642-41515-9

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation