Skip to main content
SpringerLink
Log in

Finite Differences Method for the First Order 2-D Partial Equation

  • Conference paper
Numerical Analysis and Its Applications (NAA 2012)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 8236))

Included in the following conference series:

  • 3205 Accesses

Abstract

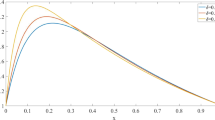
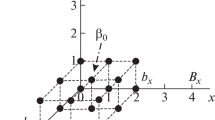
In this study a new method for finding exact solution of the Cauchy problem subject to a discontinuous initial profile for the two dimensional scalar conservation laws is suggested. For this aim, first, some properties of the weak solution of the linearized equation are investigated. Taking these properties into consideration an auxiliary problem having some advantages over the main problem is introduced. The proposed auxiliary problems also permit us to develop effective different numerical algorithms for finding the solutions. Some computer experiments are carried out.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 39.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

References

  1. Kurganov, A., Tadmor, E.: Solution of Two-Dimensional Riemann Problems for Gas Dynamics without Riemann Problem. Numerical Methods for Partial Differential Equations 18, 548–608 (2002)

    Article  MathSciNet  Google Scholar 

  2. Levy, D., Puppo, G., Russo, G.: A third order central WENO scheme for 2D conservation laws. Applied Numerical Mathematics 33, 415–421 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  3. Yoon, D., Hwang, W.: Two- Dimensional Riemann Problem for Burger’s Equation. Bull. Korean Math. Soc. 45(1), 191–205 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  4. Godlewski, E., Raviart, R.E.: Hyperbolic Systems of Conservation Laws. Mathematiques & Applications (1991)

    Google Scholar 

  5. Godunov, S.K.: A Difference Scheme for Numerical Computation of Discontinuous Solutions of Equations of Fluid Dynamics. Mat. Sb. 47(89), 271–306 (1959)

    MathSciNet  Google Scholar 

  6. Kroner, D.: Numerical Schemes for Conservation Laws. J.Wiley & Sons Ltd. and B.G. Tenber (1997)

    Google Scholar 

  7. Kruzkov, S.N.: First Order Quasilinear Equation in Several Independent Variables. Math. Sbornik 81, 217–243 (1970)

    Article  MathSciNet  Google Scholar 

  8. Lax, P.D.: Weak Solutions of Nonlinear Hyperbolic Equations and Their Numerical Computations

    Google Scholar 

  9. LeVeque, R.J.: Finite Volume Methods for Hyperbolic Problems, 558 p. Cambridge University Press (2002)

    Google Scholar 

  10. Oleinik, O.A.: Discontinuous Solutions of Nonlinear Differential Equations. Usp. Math. Nauk 12 (1957)

    Google Scholar 

  11. Rasulov, M.A., et al.: Identification of the Saturation Jump in the Process of Oil Displacement by Water in a 2D Domain. Dokl RAN, USSR 319(4), 943–947 (1991)

    MathSciNet  Google Scholar 

  12. Toro, E.F., Titarev, V.A.: ADER Schemes for Scalar Non-linear Hyperbolic Conservation Laws with Source Terms in Three-space Dimensions. J. Comput. Phys. 202(1), 196–215 (2005)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Computing, Beykent University, Sisli-Ayazaga Campus, 34396, Istanbul, Turkey

    Mahir Rasulov

  2. Department of Physics, Yildiz Technical University, Istanbul, Turkey

    E. Ilhan Sahin

  3. Zorlu Holding, Istanbul, Turkey

    M. Gokhan Soguksu

Authors
  1. Mahir Rasulov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. Ilhan Sahin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Gokhan Soguksu
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Institute of Information and Communication Technlogies, Bulgarian Academy of Sciences, Acad. G. Bonchev, Bl25A, 1113, Sofia, Bulgaria

    Ivan Dimov

  2. Department of Applied Analysis, Pázm\’{a}ny P\’{e}ter s\’{e}t\’{a}ny 1/C,, Eötvös Loránd University, 1117, Budapest, Hungary

    István Faragó

  3. University of Rousse, 8 Studentska Str.,, 7017, Rousse, Bulgaria

    Lubin Vulkov

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Rasulov, M., Sahin, E.I., Soguksu, M.G. (2013). Finite Differences Method for the First Order 2-D Partial Equation. In: Dimov, I., Faragó, I., Vulkov, L. (eds) Numerical Analysis and Its Applications. NAA 2012. Lecture Notes in Computer Science, vol 8236. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-41515-9_51

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-41515-9_51

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-41514-2

  • Online ISBN: 978-3-642-41515-9

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation