Abstract
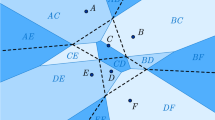
The notion of Voronoi diagrams refer to a conceptually simple geometric construct that is based on a finite set of points in a Euclidean space. Intuitively speaking, it is such a simple notion that it can be described to a non-specialist. Indeed even some social and cultural settings can be described that would convey the essence of the concept. Consider for instance a number of strangers who are standing still in a room at random locations. In what region of space can an individual freely move his/her arms without appearing to be impolite to the others? Without having a precise definition of this personal space, each individual would most likely have an intuitive notion of it. If each individual is reduced to a single point occupying a specific location in the room, the personal space of a particular point is its Voronoi cell, the set of all points that are closer to that point than to any of the other points. Each Voronoi cell is a polyhedral region. The Voronoi diagram of the set of points is the partitioning of the space into the collection of Voronoi cells, together with their boundaries.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Kalantari, B.: Polynomial Root-Finding and Polynomiography. World Scientific, New Jersey (2008)
Kalantari, B.: Polynomiography: From the fundamental theorem of algebra to art. LEONARDO 38, 233–238 (2005)
Kalantari, B.: Voronoi diagrams and polynomial root-finding. In: International Symposium on Voronoi Diagrams, pp. 31–40 (June 2009)
Kalantari, B.: Polynomial root-finding methods whose basins of attraction approximate voronoi diagram. Discrete & Computational Geometry 46(1), 187–203 (2011)
Asano, T.: Matoušek, J., Tokuyama, T.: Society for Industrial and Applied Mathematics
de Biasi, S.C., Kalantari, B., Kalantari, I.: Mollified zone diagrams and their computation. In: Gavrilova, M.L., Tan, C.J.K., Mostafavi, M.A. (eds.) Transactions on Computational Science XIV. LNCS, vol. 6970, pp. 31–59. Springer, Heidelberg (2011)
Kalantari, B.: A characterization theorem and an algorithm for a convex hull problem (2012), arxiv.org/pdf/1204.1873v2.pdf
Gavrilova, M. (ed.): Generalized Voronoi Diagram: A Geometry-Based Approach to Computational Intelligence. Springer (2008)
Luchnikov, V.A., Gavrilova, M.L., Medvedev, N.N., Voloshin, V.P.: The voronoi-delaunay approach for the free volume analysis of a packing of balls in a cylindrical cylindrical container. Future Generation Comp. Syst. 18, 673–679 (2002)
Gavrilova, M.L., Ratschek, H., Rokne, J.G.: Exact computation of delaunay and power triangulations. Reliable Computing 6(1), 39–60 (2000)
Gavrilova, M.L., Rokne, J.: Collision detection optimization in a multi-particle system. In: Sloot, P.M.A., Tan, C.J.K., Dongarra, J., Hoekstra, A.G. (eds.) ICCS 2002, Part III. LNCS, vol. 2331, pp. 105–114. Springer, Heidelberg (2002)
Gavrilova, M.L., Rokne, J.G.: Collision detection optimization in a multi-particle system. J. Comput. Geometry Appl. 13, 279–302 (2003)
Wang, C., Gavrilova, M.L.: Delaunay triangulation algorithm for fingerprint matching. In: ISVD, pp. 208–216 (2006)
Wang, C., Gavrilova, M.L., Luo, Y., Rokne, J.G.: An efficient algorithm for fingerprint matching. In: International Conference on Pattern Recognition ICPR, pp. 1034–1037. IEEE-CS (2006)
Bhattacharya, P., Gavrilova, M.L.: Crystal - a new density-based fast and efficient clustering algorithm. In: ISVD, pp. 102–111 (2006)
Xuan, K., Zhao, G., Taniar, D., Srinivasan, B., Safar, M., Gavrilova, M.L.: Network voronoi diagram based range search. In: AINA, pp. 741–748 (2009)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Kalantari, B. (2013). The State of the Art of Voronoi Diagram Research. In: Gavrilova, M.L., Tan, C.J.K., Kalantari, B. (eds) Transactions on Computational Science XX. Lecture Notes in Computer Science, vol 8110. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-41905-8_1
Download citation
DOI: https://doi.org/10.1007/978-3-642-41905-8_1
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-41904-1
Online ISBN: 978-3-642-41905-8
eBook Packages: Computer ScienceComputer Science (R0)