Skip to main content
Springer Nature Link
Log in

Model Counting for Formulas of Bounded Clique-Width

  • Conference paper
Algorithms and Computation (ISAAC 2013)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 8283))

Included in the following conference series:

  • 1658 Accesses

Abstract

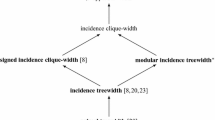
We show that #SAT is polynomial-time tractable for classes of CNF formulas whose incidence graphs have bounded symmetric clique-width (or bounded clique-width, or bounded rank-width). This result strictly generalizes polynomial-time tractability results for classes of formulas with signed incidence graphs of bounded clique-width and classes of formulas with incidence graphs of bounded modular treewidth, which were the most general results of this kind known so far.

This research was supported by the ERC (COMPLEX REASON, 239962).

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Bacchus, F., Dalmao, S., Pitassi, T.: Algorithms and complexity results for #SAT and Bayesian inference. In: 44th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2003), pp. 340–351 (2003)

    Google Scholar 

  2. Bui-Xuan, B.-M., Telle, J.A., Vatshelle, M.: H-join decomposable graphs and algorithms with runtime single exponential in rankwidth. Discrete Applied Mathematics 158(7), 809–819 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bui-Xuan, B.-M., Telle, J.A., Vatshelle, M.: Boolean-width of graphs. Theoretical Computer Science 412(39), 5187–5204 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  4. Courcelle, B.: Clique-width of countable graphs: a compactness property. Discrete Mathematics 276(1-3), 127–148 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  5. Hliněný, P., Oum, S.I.: Finding branch-decompositions and rank-decompositions. SIAM J. Comput. 38(3), 1012–1032 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  6. Fischer, E., Makowsky, J.A., Ravve, E.R.: Counting truth assignments of formulas of bounded tree-width or clique-width. Discr. Appl. Math. 156(4), 511–529 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  7. Ganian, R., Hliněný, P.: On parse trees and Myhill-Nerode-type tools for handling graphs of bounded rank-width. Discr. Appl. Math. 158(7), 851–867 (2010)

    Article  MATH  Google Scholar 

  8. Ganian, R., Hliněný, P., Obdrzálek, J.: Better algorithms for satisfiability problems for formulas of bounded rank-width. Fund. Inform. 123(1), 59–76 (2013)

    MathSciNet  MATH  Google Scholar 

  9. Gaspers, S., Szeider, S.: Strong backdoors to bounded treewidth SAT. In: Proceedings of FOCS 2013, The 54th Annual Symposium on Foundations of Computer Science, Berkeley, California, USA (to appear, 2013)

    Google Scholar 

  10. Gottlob, G., Pichler, R.: Hypergraphs in model checking: acyclicity and hypertree-width versus clique-width. SIAM J. Comput. 33(2), 351–378 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  11. Nishimura, N., Ragde, P., Szeider, S.: Solving #SAT using vertex covers. Acta Informatica 44(7-8), 509–523 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  12. Ordyniak, S., Paulusma, D., Szeider, S.: Satisfiability of acyclic and almost acyclic CNF formulas. Theoretical Computer Science 481, 85–99 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  13. Paulusma, D., Slivovsky, F., Szeider, S.: Model counting for CNF formulas of bounded modular treewidth. In: Portier, N., Wilke, T. (eds.) Proceedings of STACS 2013. LIPIcs, vol. 20, pp. 55–66. Leibniz-Zentrum fuer Informatik (2013)

    Google Scholar 

  14. Roth, D.: On the hardness of approximate reasoning. Artificial Intelligence 82(1-2), 273–302 (1996)

    Article  MathSciNet  Google Scholar 

  15. Samer, M., Szeider, S.: Algorithms for propositional model counting. J. Discrete Algorithms 8(1), 50–64 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  16. Sang, T., Beame, P., Kautz, H.A.: Performing Bayesian inference by weighted model counting. In: Proceedings of the 20th National Conference on Artificial Intelligence, AAAI 2005, vol. 1, pp. 475–481. AAAI Press (2005)

    Google Scholar 

  17. Szeider, S.: On fixed-parameter tractable parameterizations of SAT. In: Giunchiglia, E., Tacchella, A. (eds.) SAT 2003. LNCS, vol. 2919, pp. 188–202. Springer, Heidelberg (2004)

    Chapter  Google Scholar 

  18. Valiant, L.G.: The complexity of computing the permanent. Theoretical Computer Science 8(2), 189–201 (1979)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Information Systems, Vienna University of Technology, Vienna, Austria

    Friedrich Slivovsky & Stefan Szeider

Authors
  1. Friedrich Slivovsky
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stefan Szeider
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Computer Science and Engineering, Chinese University of Hong Kong, Shatin, 100084, Hong Kong, China

    Leizhen Cai

  2. Department of Computer Science and Engineering, Hong Kong University of Science and Technology, Clear Water Bay, 100044, Hong Kong, China

    Siu-Wing Cheng

  3. Department of Computer Science, University of Hong Kong, Porfkulam, 100084, Hong Kong, China

    Tak-Wah Lam

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Slivovsky, F., Szeider, S. (2013). Model Counting for Formulas of Bounded Clique-Width. In: Cai, L., Cheng, SW., Lam, TW. (eds) Algorithms and Computation. ISAAC 2013. Lecture Notes in Computer Science, vol 8283. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-45030-3_63

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-45030-3_63

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-45029-7

  • Online ISBN: 978-3-642-45030-3

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics