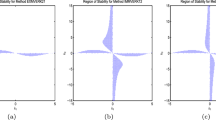
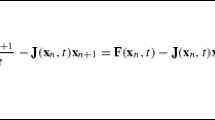Abstract
Concepts of new algorithms suitable for the integration of stiff and/or highly oscillatory problems are outlined in the first part of the paper. A common characteristics of the presented methods is, that they employ higher derivatives of the state variables which are calculated analytically by means of automated symbolic differentiation techniques. Moreover, for the solution of the system of algebraic equations, which is solved after each integration step, algebraic manipulation techniques are applied in order to derive the Jacobian of the system of ODEs. All methods have been implemented in the semianalytical simulation package PSCSP (Powers Series Continuous-System Simulation Program) [1] which provides a number of attractive features for engineering and scientific applications that are not available in other present-day simulation languages.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Ref
Ref.: H.J. Halin “The Applicability of Taylor Series Methods in Simulation” Proceedings of the 1983 Summer Computer Simulation Conference, July 11–13, 1983, Vancouver, B.C., Canada, Vol. II (State-of-the-Art Topics), pp. 1032-1078.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1985 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Halin, H.J., Tichy, K. (1985). Concepts of New Algorithms for the Integration of Stiff and/or Highly Oscillatory Problems. In: Möller, D.P.F. (eds) Simulationstechnik. Informatik-Fachberichte, vol 109. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-70640-0_37
Download citation
DOI: https://doi.org/10.1007/978-3-642-70640-0_37
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-15700-7
Online ISBN: 978-3-642-70640-0
eBook Packages: Springer Book Archive