Nonstandard Analysis-Methoden in Anwendung auf ein Eigenwertproblem der PLL Theorie

Zusammenfassung

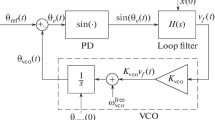
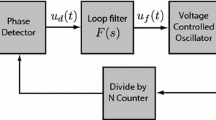
Ein Phase-Locked Loop (PLL) ist ein Regelsystem, das einen Oszillator und ein vorgegebenes Signal in Frequenz und Phase synchronisieren soll. Verläßt bei dem Nachregelungsvorgang der Phasenfehler das Ausgangsintervall [0,2π], so spricht man von „Cycle-Slipping“. In einigen Anwendungen zur Informationsübertragung (Messungen der Dopplerfrequenz), bei denen es auf eine genaue Phasenverfolgung ankommt, ist Cycle-Slipping schädlich und bedarf einer Häufigkeitsanalyse. Unter Berücksichtigung eines geeignet normierten weißen Rauschens n(t) und eines Frequenzsprunges Ω₀ am Eingang erhält man für den Phasenfehlerprozeß φ(t) bei einem PLL erster Ordnung die Differentialgleichung $\phi (t) = \Omega _0 - K(Ag(\phi ) + n(t))$ mit den Loop-Konstanten K, A und der periodischen Phasendetektorcharakteristik g(f). Die zugehörige Übergangswahrscheinlichkeitsdichtefunktion y(φ, t) genügt der Fokker-Planck Differentialgleichung, die nach Abseparat ion der Zeit folgende Form hat [FL]

$$py'' + \frac{d}{{dx}}\{ (g(x) - w)y\} = - \frac{\lambda }{4}y$$

(1)

mit der Phase x, den Randbedingungen der Periodizität der Funktion y und ihrer Ableitung, dem Eigenwert λ≥0, dem Parameter p, der für die reziproke Signal-Rausch Relation l/SNR steht und dem normierten Frequenzsprung w.