Curvature Estimation with a DCA neural network

Abstract

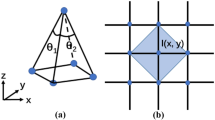
Curvature has been identified as an important feature to reconstruct properties like object shape or relative depth from two-dimensional gray scale images [6, 9]. This coincides with the assumption that curvature is processed by a separate channel in human early vision, just like contours or contrast [23, 2, 3]. The process of early vision is assumed to be divided into vision modules [15] that are evaluated independently in almost completely separate pathways [21, 5, 10]. This motivates to study how artificial neural networks can be used to mimic the operation of some of these putative modules. In this contribution we investigate to what extent curvature information can be extracted from an image, only on the basis of the gray scale pixel information. The paper shows that a neural network based on local linear maps LLM can be trained to estimate the local amount and orientation of curvature from only a small patch of grayscale pixel images. The accuracy of this estimation depends on the complexity of the surfaces. Using a recently developed approach of cascaded LLM-networks (DCA), we demonstrate that the performance that can be obtained with a standard LLM-net can be considerably improved.