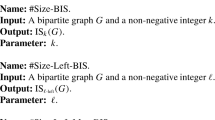Abstract
A locally-optimal structure is a combinatorial structure that cannot be improved by certain (greedy) local moves, even though it may not be globally optimal. An example is a maximal independent set in a graph. It is trivial to construct an independent set in a graph. It is easy to (greedily) construct a maximal independent set. However, it is NP-hard to construct a globally-optimal (maximum) independent set.This situation is typical. Constructing a locally-optimal structure is somewhat more difficult than constructing an arbitrary structure, and constructing a globally-optimal structure is more difficult than constructing a locally-optimal structure. The same situation arises with listing. The differences between the problems become obscured when we move from listing to counting because nearly everything is \(\#\text {P} \)-complete. However, we highlight an interesting phenomenon that arises in approximate counting, where approximately counting locally-optimal structures is apparently more difficult than approximately counting globally-optimal structures. Specifically, we show that counting maximal independent sets is complete for \(\#\text {P} \) with respect to approximation-preserving reductions, whereas counting all independent sets, or counting maximum independent sets is complete for an apparently smaller class, #RH\(\varPi _1\) which has a prominent role in the complexity of approximate counting. Motivated by the difficulty of approximately counting maximal independent sets in bipartite graphs, we also study counting problems involving minimal separators and minimal edge separators (which are also locally-optimal structures). Minimal separators have applications via fixed-parameter-tractable algorithms for constructing triangulations and phylogenetic trees. Although exact (exponential-time) algorithms exist for listing these structures, we show that the counting problems are as hard as they could possibly be. All of the exact counting problems are \(\#\text {P} \)-complete, and all of the approximation problems are complete for \(\#\text {P} \) with respect to approximation-preserving reductions. A full version [14] containing detailed proofs is available at http://arxiv.org/abs/1411.6829. Theorem-numbering here matches the full version.
L.A. Goldberg and J. Lapinskas—The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007–2013) ERC grant agreement no. 334828. The paper reflects only the authors’ views and not the views of the ERC or the European Commission. The European Union is not liable for any use that may be made of the information contained therein.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Berry, A., Bordat, J.P., Cogis, O.: Generating all the minimal separators of a graph. International Journal of Foundations of Computer Science 11(3), 397–403 (2000)
Bodlaender, H.L., Fomin, F.V.: Tree decompositions with small cost. Discrete Applied Mathematics 145(2), 143–154 (2005)
Bodlaender, H.L., Fomin, F.V., Koster, A.M., Kratsch, D., Thilikos, D.M.: On exact algorithms for treewidth. ACM Trans. Algorithms 9(1), 12:1–12:23 (2012)
Bodlaender, H.L., Koster, A.M.: Combinatorial optimization on graphs of bounded treewidth. The Computer Journal 51(3), 255–269 (2008)
Bouchitté, V., Todinca, I.: Treewidth and minimum fill-in: grouping the minimal separators. SIAM Journal on Computing 31(1), 212–232 (2001)
Bouchitté, V., Todinca, I.: Listing all potential maximal cliques of a graph. Theoretical Computer Science 276(1–2), 17–32 (2002)
Diestel, R.: Graph Theory, 4th Edition. Graduate texts in mathematics, vol. 173. Springer (2012)
Dyer, M., Goldberg, L.A., Greenhill, C., Jerrum, M.: The relative complexity of approximate counting problems. Algorithmica 38(3), 471–500 (2004)
Fomin, F.V., Kratsch, D., Todinca, I., Villanger, Y.: Exact algorithms for treewidth and minimum fill-in. SIAM Journal on Computing 38(3), 1058–1079 (2008)
Fomin, F.V., Villanger, Y.: Finding induced subgraphs via minimal triangulations. In: 27th STACS, pp. 383–394 (2010)
Fomin, F.V., Villanger, Y.: Treewidth computation and extremal combinatorics. Combinatorica 32(3), 289–308 (2012)
Furuse, M., Yamazaki, K.: A revisit of the scheme for computing treewidth and minimum fill-in. Theoretical Computer Science 531(0), 66–76 (2014)
Goldberg, L.A.: Efficient Algorithms for Listing Combinatorial Structures. Cambridge University Press (1993). Cambridge Books Online
Goldberg, L.A., Gysel, R., Lapinskas, J.: Approximately counting locally-optimal structures. CoRR abs/1411.6829 (2014)
Goldberg, L.A., Jerrum, M.: The complexity of ferromagnetic Ising with local fields. Combin. Probab. Comput. 16(1), 43–61 (2007)
Goldberg, L.A., Jerrum, M.: Approximating the partition function of the ferromagnetic Potts model. J. ACM 59(5), 31 (2012). Art. 25
Gysel, R.: Unique perfect phylogeny characterizations via uniquely representable chordal graphs. CoRR abs/1305.1375 (2013)
Gysel, R.: Minimal triangulation algorithms for perfect phylogeny problems. In: Dediu, A.-H., Martín-Vide, C., Sierra-Rodríguez, J.-L., Truthe, B. (eds.) LATA 2014. LNCS, vol. 8370, pp. 421–432. Springer, Heidelberg (2014)
Johnson, D.S., Papadimitriou, C.H., Yannakakis, M.: How easy is local search? J. Comput. Syst. Sci. 37(1), 79–100 (1988)
Kashiwabara, T., Masuda, S., Nakajima, K., Fujisawa, T.: Generation of maximum independent sets of a bipartite graph and maximum cliques of a circular-arc graph. J. Algorithms 13(1), 161–174 (1992)
Kloks, T., Kratsch, D.: Listing all minimal separators of a graph. SIAM Journal on Computing 27, 605–613 (1998)
Lokshtanov, D.: On the complexity of computing treelength. Discrete Applied Mathematics 158(7), 820–827 (2010)
Schäffer, A.A., Yannakakis, M.: Simple local search problems that are hard to solve. SIAM J. Comput. 20(1), 56–87 (1991)
Shen, H., Liang, W.: Efficient enumeration of all minimal separators in a graph. Theoretical Computer Science 180(1–2), 169–180 (1997)
Takata, K.: Space-optimal, backtracking algorithms to list the minimal vertex separators of a graph. Discrete Appl. Math. 158(15), 1660–1667 (2010)
Tsukiyama, S., Ide, M., Ariyoshi, H., Shirakawa, I.: A new algorithm for generating all the maximal independent sets. SIAM J. Comput. 6(3), 505–517 (1977)
Vadhan, S.P.: The complexity of counting in sparse, regular, and planar graphs. SIAM J. Comput. 31(2), 398–427 (2001)
Whitney, H.: Planar graphs. Fundamenta Mathematicae 21(1), 73–84 (1933)
Zuckerman, D.: On unapproximable versions of NP-complete problems. SIAM J. Comput. 25(6), 1293–1304 (1996)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Goldberg, L.A., Gysel, R., Lapinskas, J. (2015). Approximately Counting Locally-Optimal Structures. In: Halldórsson, M., Iwama, K., Kobayashi, N., Speckmann, B. (eds) Automata, Languages, and Programming. ICALP 2015. Lecture Notes in Computer Science(), vol 9134. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-47672-7_53
Download citation
DOI: https://doi.org/10.1007/978-3-662-47672-7_53
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-47671-0
Online ISBN: 978-3-662-47672-7
eBook Packages: Computer ScienceComputer Science (R0)