Adaptive Security with Quasi-Optimal Rate

Abstract

A multiparty computation protocol is said to be adaptively secure if it retains its security in the presence of an adversary who can adaptively corrupt participants as the protocol proceeds. This is in contrast to a static corruption model where the adversary is forced to choose which participants to corrupt before the protocol begins. A central tool for constructing adaptively secure protocols is non-committing encryption (Canetti, Feige, Goldreich and Naor, STOC ’96). The original protocol of Canetti et al. had ciphertext expansion $\mathcal {O}(k^2)$ where $k$ is the security parameter, and prior to this work, the best known constructions had ciphertext expansion that was either $\mathcal {O}(k)$ under general assumptions, or alternatively $\mathcal {O}(\log (n))$, where n is the length of the message, based on a specific factoring-based hardness assumption.

In this work, we build a new non-committing encryption scheme from lattice problems, and specifically based on the hardness of (Ring) Learning With Errors (LWE). Our scheme achieves ciphertext expansion as small as $\mathrm{polylog}(k)$. Moreover when instantiated with Ring-LWE, the public-key is of size $\mathcal {O}(n\mathrm{polylog}(k))$. All previously proposed schemes had public-keys of size $\varOmega (n^2\mathrm{polylog}(k))$.

R. Ostrovsky—Work done in part while visiting Simons Institute in Berkeley and supported in part by NSF grants 09165174, 1065276, 1118126 and 1136174, US-Israel BSF grant 2008411, OKAWA Foundation Research Award, IBM Faculty Research Award, Xerox Faculty Research Award, B. John Garrick Foundation Award, Teradata Research Award, and Lockheed-Martin Corporation Research Award. This material is based upon work supported in part by DARPA Safeware program. The views expressed are those of the author and do not reflect the official policy or position of the Department of Defense or the U.S. Government.

S. Richelson—Part of this work done while visiting IDC Herzliya, supported by the European Research Council under the European Unions Seventh Framework Programme (FP 2007–2013), ERC Grant Agreement n. 307952.

A. Rosen—Efi Arazi School of Computer Science, IDC Herzliya, Israel. Work supported by ISF grant no.1255/12 and by the ERC under the EU’s Seventh Framework Programme (FP/2007–2013) ERC Grant Agreement n. 307952. Work in part done while the author was visiting the Simons Institute for the Theory of Computing, supported by the Simons Foundation and by the DIMACS/Simons Collaboration in Cryptography through NSF grant #CNS-1523467.

1 Introduction

Secure multiparty computation (MPC) allows a group of players to compute any joint function of their private inputs, even when some of the players are adversarial [GMW87, BGW88, CCD88]. MPC protocols are often categorized based on the security properties they offer. One natural and well-studied distinction is between protocols which are secure against an adaptive adversary, and those which are only secure when the adversary is static. A static adversary is one who chooses which parties to corrupt before the protocol begins, while an adaptive adversary can choose which parties to corrupt on the fly, and thus the corruption pattern may depend on the messages exchanged during the protocol. Adaptive security is desirable as it models real-world adversarial behavior more honestly. Unfortunately, adaptively secure protocols are significantly harder to construct as several techniques from the literature for proving security in the static model do not seem to carry over to the adaptive model.

Adaptively Secure MPC. The information-theoretic MPC protocol of [BGW88] is adaptively secure when each pair of parties is connected by a secure channel (so communication between honest parties may not be observed by the adversary). Roughly, this is because for a security threshold of t, the views of any t players are statistically independent of the secret inputs of all other parties. Thus the information the adversary obtains from corrupting fewer than t parties can be simulated and so adaptively choosing new parties to corrupt does not provide an advantage. One might hope to obtain an adaptively secure protocol in the plain model (i.e. without ideal channels) by using semantically secure encryption. Specifically, each pair of parties might first exchange public keys and then communicate “privately” by publicly broadcasting encryptions of their messages. The ideal adversary might then be able to emulate a real interaction by broadcast encryptions of zero, and prove indistinguishability using semantic security. However, as pointed out in [CFGN96], this intuition does not exactly work. Essentially the problem is that the ciphertext in ordinary encryption “commits” the sender to one message. An ideal adversary, therefore, would be unable to open an encryption of zero to anything except zero. This is problematic for adaptive security because if a party is corrupted after it has already sent encryptions, then upon learning the secret keys and previously used randomness, the adversary will be able to tell if it is in the ideal or real world based on whether the entire communication is encryptions of zero or not. [CFGN96] goes on to define and construct a stronger type of encryption called non-committing encryption (NCE) which allows the above intuition to go through.

Non-Committing Encryption. An encryption scheme is non-committing if a simulator can geterate a public key/ciphertext pair that is indistinguishable from a real public key/ciphertext, but for which it can later produce a secret key/encryption randomness pair which “explains” the ciphertext as an encryption of any adversarily chosen message. This provides a natural method for creating adaptively secure MPC protocols: first design a statically secure protocol in the private channels model, then instantiate the private channels with NCE.

Prior Work on NCE. The original work of [CFGN96] gives an NCE protocol based on the existence of a special type of trapdoor permutations and is relatively inefficient: requiring a sender to send a ciphertext of size $\mathcal {O}(k^2)$ to encrypt a single bit (for security parameter $k$). In other words, its ciphertext expansion factor is $\mathcal {O}(k^2)$. Choi, Dachman-Soled, Malkin and Wee [CDSMW09] construct an NCE protocol with ciphertext expansion $\mathcal {O}(k)$ starting from any obvliviously-samplable cryptosystem. The paradigm of using obliviously-samplable encryption to achieve adaptive security goes back to [DN00] who give a three-round protocol which adaptively, securely realizes the ideal message transmission functionality (thus, allowing for adaptively secure MPC). [DN00] show how to instantiate obvliviously-samplable encryption based on a variety of assumptions, building on an earlier work of Beaver [Bea97], which essentially constructs obvliviously-samplable encryption assuming DDH. Very recently, Hemenway, Ostrovsky and Rosen [HOR15] construct an NCE protocol with logarithmic expansion based on the $\varPhi -$hiding assumption, which is related to (though generally believed to be stronger than) RSA.

See Fig. 1 for a comparison of past and current work on NCE.

Fig. 1.

Comparison to prior work. The parameter $k$ denotes the security parameter, and n denotes the message length.

1.1 Our Contribution

In this work, we construct an NCE scheme with polylogarithmic ciphertext expansion and which improves upon the recent work of [HOR15] in a number of ways.

• Assumption: Learning with errors (LWE) [Reg09] is known to be as hard as worst-case lattice problems, and is widely accepted as a cryptographic hardness assumption. Its ring variant is as hard as worst-case problems on ideal lattices and is widely used in practice as it allows representing a vector consicely as a single ring element. For comparison, the $\varPhi -$hiding assumption is not as widely used or accepted, and certain choices of parameters must be carefully avoided as they are susceptible to polynomial time attacks.

• Smaller Public Keys: When instantiated with Ring-LWE, the public-key of our scheme is of size $\mathcal {O}(n\mathrm{polylog}(k))$. All previously proposed schemes had public-keys of size $\varOmega (n^2\mathrm{polylog}(k))$.

• No Sampling Issues: One subtle shortcoming of the [HOR15] work is that the non-committing property of their encryption scheme necessitates the existence of a public modulus N whose factorization is not known. This means that in order to attain full simulatability the modulus N will have to be sampled jointly by the parties, using a secure protocol (which itself needs to be made adaptively secure). Our current work, in contrast, does not suffer from this shortcoming and does not necessitate joint simulation of the public parameters.

1.2 Our Construction

For this high-level description of our protocol we assume familiarity with the definition of non-committing encryption as well as Regev’s LWE-based encryption scheme [Reg09], and Micciancio-Peikert trapdoors for LWE [MP12]. We refer the reader to Sect. 2 or the papers themselves for more information on these topics.

KeyGen. Let q, m, k be LWE parameters and n a parameter linear in the message length $\ell$. The receiver chooses a random subset $I_R\subset \{1,\dots ,n\}$ of size n / 8, a matrix $\mathbf {A}\in {\mathbb Z}_q^{m\times k}$ and vectors $\mathbf {v}_1,\dots ,\mathbf {v}_n\in {\mathbb Z}_q^m$, where $\mathbf {v}_i$ is an LWE instance if $i\in I_R$ and is random otherwise. The public key is $\bigl (\mathbf {A},\mathbf {v}_1,\dots ,\mathbf {v}_n\bigr )$ and the secret key is $\bigl (I_R,\{\mathbf {s}_i\}_{i\in I_R}\bigr )$ where $\mathbf {s}_i\in {\mathbb Z}_q^k$ is the LWE secret for $\mathbf {v}_i$. So receiver has generated n Regev public keys, but for which it only knows n / 8 of the corresponding secret keys.

Enc. Let $\mathsf{msg}\in \{0,1\}^\ell$ be a plaintext, and let $y=(y_1,\dots ,y_n)=\mathbf {ECC}(\mathsf{msg})\in \{0,1\}^n$ be the image of $\mathsf{msg}$ under a suitable error-correcting code. The sender chooses a random subset $I_S\subset \{1,\dots ,n\}$ of size n / 8 and generates Regev encryptions, under public key $(\mathbf {A},\mathbf {v}_i)$ of $y_i$ if $i\in I_S$ or of a random bit if $i\notin I_S$. Important for the efficiency of our protocol is that these encryptions be generated using shared randomness. Specifically, the sender chooses a random short $\mathbf {r}\in {\mathbb Z}_q^m$ and constructs the ciphertext $(\mathbf {u},w_1,\dots ,w_n)$ where $\mathbf {u}=\mathbf {r}^\mathsf{t}\mathbf {A}\in {\mathbb Z}_q^k$ and $w_i=\mathbf {r}^\mathsf{t}\mathbf {v}_i+e_i+\bigl (q/2\bigr )z_i$ where $z_i=y_i$ if $i\in I_S$ and is random otherwise (the $e_i$ are short Gaussian errors). So sender has encrypted a string $z\in \{0,1\}^n$ which agrees with y in 9n / 16 of the positions on expectation. The encryption randomness consists of $\mathbf {r}$, $I_S$ as well as the Gaussian errors.

Dec. Given a ciphertext $(\mathbf {u},w_1,\dots ,w_n)$ and secret key $\bigl (I_R,\{\mathbf {s}_i\}_{i\in I_R}\bigr )$, receiver constructs $y'\in \{0,1\}^n$ by setting $y_i'=\big \lfloor \bigl (2/q\bigr )(w_i-\mathbf {u}^\mathsf{t}\mathbf {s}_i)\big \rceil$ if $i\in I_R$ and $y_i'$ to be a random bit otherwise. Then receiver decodes $y_i'$ and outputs $\mathsf{msg}'\in \{0,1\}^\ell$. So receiver is decrypting the ciphertexts for which he knows the secret key, and is completing this to a string in $\{0,1\}^n$ by filling in the remaining positions randomly.

Correctness. Let $y=\mathbf {ECC}(\mathsf{msg})\in \{0,1\}^n$ be the coded message and let $y'\in \{0,1\}^n$ be the string obtained during decryption. Note that whenever $i\in I_R\cap I_S$, $y_i=y_i'$ with high probability, and whenever $i\notin I_R\cap I_S$ $y_i=y_i'$ with probability 1 / 2. Therefore, $y_i=y_i'$ for 65n / 128 of the values $i\in \{1,\dots ,n\}$ on expectation. It can be shown using the tail bound (Lemma 1), that there exists a constant $\delta >0$ such that $y_i=y_i'$ for at least $(1/2+\delta )n$ values of i with high probability. By our choice of error correcting code, we can decode given such a tampered codeword.

Adversary’s Real World View. The non-committing adversary receives the secret key and encryption randomness and tries to use these values to distinguish the real and ideal worlds. The most difficult aspects of the real world view to simulate are the subsets $I_R,I_S\subset \{1,\dots ,n\}$. In the real world, both sets are random of size n / 8 and so the size of their intersection is a hypergeometric random variable. This must be replicated in the ideal world in order for indistinguishability to hold. To complicate matters, it is important that the right number of $i\in I_R\cap I_S$ are such that $y_i=0$ and $y_i'=0$. Likewise, we must make sure that the right number of $i\in I_R\cap \overline{I_S}$ are such that $y_i=0$ and $y_i'=1$, and so on. This involves carefully computing the multivariate hypergeometric distribution which arises from the real world execution so that we may emulate it in the ideal world. We will leave out most of the details for this overview; the specifics are given in Sect. 3.

Simulating the Public Key and Ciphertext. The simulator chooses a partition $I_\mathsf{good}\cup I_\mathsf{bad}=\{1,\dots ,n\}$ at random, and chooses vectors $\mathbf {v}_1,\dots ,\mathbf {v}\in {\mathbb Z}_q^m$ so it knows an LWE secret $\mathbf {s}_i$ for $\mathbf {v}_i$ whenever $i\in I_\mathsf{good}$, and so that it knows an MP trapdoor for the matrix $\hat{\mathbf {A}}=\bigl [\mathbf {A}|\mathbf {V}\bigr ]$ where the columns of $\mathbf {V}$ are $\{\mathbf {v}_i\}_{i\in I_\mathsf{bad}}$. The sets $I_\mathsf{good}$ and $I_\mathsf{bad}$ correspond to the $i\in \{1,\dots ,n\}$ for which it knows/doesn’t know a secret key. It is important for simulation that $I_\mathsf{good}$ is much larger than $I_R$. A good choice, for example is $|I_\mathsf{good}|=3n/4$. The simulator then sets its public key to $(\mathbf {A},\mathbf {v}_1,\dots ,\mathbf {v}_n)$. It further partitions $I_\mathsf{good}$ into $I_{\mathsf{good},0}\cup I_{\mathsf{good},1}$ and sets the ciphertext $(\mathbf {u},w_1,\dots ,w_n)$ to be so that $\mathbf {u}=\mathbf {r}^\mathsf{t}\mathbf {A}$ and $w_i$ is a valid Regev encryption of 0 (resp. 1) if $i\in I_{\mathsf{good},0}$ (resp. $i\in I_{\mathsf{good},1}$), and $w_i$ is random if $i\in I_\mathsf{bad}$.

Simulating the Secret Key and Decryption Randomness. Upon receiving $\mathsf{msg}$, the simulator sets $(y_1,\dots ,y_n)=\mathbf {ECC}(\mathsf{msg})\in \{0,1\}^n$ and must produce $I_R,I_S\subset \{1,\dots ,n\}$, string $y'\in \{0,1\}^n$ and short $\mathbf {r}\in {\mathbb Z}_q^m$ which look like the quantities which arise from a real world execution (we ignore the Gaussian errors in this discussion). The simulator must choose $I_R\subset I_\mathsf{good}$ since the $\mathbf {v}_i$ for $i\in I_\mathsf{bad}$ are “lossy” and so have no secret keys (this is why we chose $I_\mathsf{good}$ much larger than  $I_R$). The simulator must also choose $y_i'=b$ for $i\in I_{\mathsf{good},b}$, since these $w_i$ are valid encryptions of b. More subtly, the simulator must make sure to choose $y'$ so that the number of i for which $y_i'=0$ and $i\in I_R$ is as in the real world. As mentioned above, this more delicate than one might think; see the paragraph below for an example. Finally, the simulator sets $I_S$ to be a subset of $\{i:y_i=y_i'\}$ of appropriate size and so the sizes of its intersections with the sets chosen so far are distributed as in the real world. Finally, the simulator sets $y_i'$ for $i\in I_\mathsf{bad}$ to be as needed to complete the real world view. Note the simulator has a trapdoor for $\hat{\mathbf {A}}$ and so may choose short $\mathbf {r}\in {\mathbb Z}_q^m$ so that $\mathbf {r}^\mathsf{t}\hat{\mathbf {A}}$ is as he chooses.

We conclude this discussion with an example which illustrates the care required to make the above proof go through. For ease of this discussion, we let $y'=y$, even though this is not true for our construction (which makes it even more complicated). Consider only the choice of $I_R$ and the number of $i\in I_R$ such that $y_i=0$. In the real world, $I_R$ is chosen randomly from $\{1,\dots ,n\}$, and since $y_i=0$ for exactly n / 2 of the $i\in \{1,\dots ,n\}$ ($\mathbf {ECC}$ is balanced), $\text {}^\#\{i\in I_R:y_i=0\}$ is distributed according to the hypergeometric distribution $\mathsf{H}\bigl (\frac{n}{8},\frac{n}{2}, n\bigr )$. In the ideal world, $I_R$ is chosen randomly from $I_\mathsf{good}$ which is itself partitioned into $I_{\mathsf{good},0}$ and $I_{\mathsf{good},1}$ of equal size so that $y_i=b$ for all $i\in I_{\mathsf{good},b}$. Therefore, in the ideal world $\text {}^\#\{i\in I_R:y_i=0\}$ is distributed according to the hypergeometric distribution $\mathsf{H}\bigl (\frac{n}{8},\frac{3n}{8},\frac{3n}{4} \bigr )$. While the expectations are equal, the random variables themselves are not and so $I_R$ must be chosen in the ideal world carefully in order to emulate the real world successfully. Details are in Sect. 3.

2 Preliminaries

2.1 Notation

If A is a Probabilistic Polynomial Time (PPT) machine, then we use to denote running the machine A and obtaining an output, where a is distributed according to the internal randomness of A. If R is a set, we use to denote sampling uniformly from R. If R and X are sets then we use the notation $\Pr _{r,x}\bigl [A(x,r)=c\bigr ]$ to denote the probability that A outputs c when x is sampled uniformly from X and r is sampled uniformly from R. A function is said to be negligible if it vanishes faster than the inverse of any polynomial. For simplicity, we often suppress random inputs to functions. In such cases, we use a semicolon to separate optional random inputs. Thus and $c = {\mathsf {Enc}}(pk,m;r)$ both indicate an encryption of m under the public key pk, but in the first case, we consider ${\mathsf {Enc}}$ as a randomized algorithm, and in the second we consider ${\mathsf {Enc}}$ as a deterministic algorithm depending on the randomness r.

2.2 Non-Committing Encryption

Non-committing encryption was introduced by Canetti, Feige, Goldreich and Naor in [CFGN96] as a primitive which allows one compile a protocol which is adaptively secure as long as all pairs of parties are connected with a secure channel, into an adaptively secure protocol in the plain model. The following definition is from [DN00] and is consistent with this viewpoint.

Definition 1

(Non-Committing Encryption). We say that a two party protocol $\varPi$ is a non-committing encryption scheme if it adaptively, securely realizes the message transmission functionality:

$$\begin{aligned} f(m,\bot )=(\bot ,m). \end{aligned}$$

The following indistinguishability based definition is sufficient and easier to work with. In our proof of security we will this second definition in its game form.

Definition 2

A cryptosystem is called non-committing, if there exists a PPT simulator ${\mathsf {Sim}}= ({\mathsf {Sim}}_1,{\mathsf {Sim}}_2)$ with the following properties:

• 1. Efficiency: The algorithms ${\mathsf {Gen}},{\mathsf {Enc}},{\mathsf {Dec}}$ and ${\mathsf {Sim}}$ are all PPT.

• 2. Correctness: For any message $m \in \mathcal {M}(\mathsf {pp})$

  

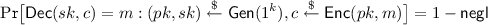
• 3. Simulatability: For any PPT adversary $\mathcal {A}$, the distributions $\varLambda ^{\mathrm {Ideal}}$ and $\varLambda ^{\mathrm {Real}}$ are computationally indistinguishable where

  

  and

  

Note that semantic security follows from simulatability.

2.3 Learning with Errors

The learning with errors (LWE) problem [Reg09] is specified by the security parameter k, a modulus q and an error distribution $\chi$ over ${\mathbb Z}_q$. In this paper our errors will be drawn exclusively from discrete Gaussians. We specify the discrete Gaussian with standard deviation $\sigma$ by $\chi _\sigma$. In its decisional form, the problem asks one to distinguish, for a random $\mathbf {s}\in {\mathbb Z}_q^k$, between the distribution $\mathsf{A}_{\mathbf {s},\chi }$ from $\mathsf{Unif}\bigl ({\mathbb Z}_q^k\times {\mathbb Z}_q\bigr )$ where $\mathsf{A}_{\mathbf {s},\chi }=\big \{(\mathbf {a},\langle \mathbf {a},\mathbf {s} \rangle +e)\big \}_{\mathbf {a}\leftarrow {\mathbb Z}_q^k,e\leftarrow \chi }$. Several important results [Reg09, Pei09, BLP13] establish the hardness of decisional LWE based on worst-case lattice problems. The following fact is standard.

Fact 1

Let $q=k^{\omega (1)}$ be superpolynomial in the security parameter k. Let $B,\sigma <q$ be such that $\sigma /B=k^{\omega (1)}$, and let $\chi$ be a $B-$bounded distribution. Then with high probability over $e\leftarrow \chi$, we have $\chi _\sigma \approx _\mathsf{s}e+\chi _\sigma$.

Ring LWE. The ring variant of LWE [LPR13] is often used in practice as it allows representing vectors succinctly as ring elements. The vectors in the usual LWE problem formulated above are replaced by elements in the quotient ring $R={\mathbb Z}[x]/\varPhi (x)$ for an irreducible cyclotomic polynomial $\varPhi$ (often $\varPhi (x)=x^\ell +1$ for $\ell$ a power of 2). Cryptographic schemes instantiated using ring LWE often are considerably more efficient than the corresponding constructions over ordinary LWE. If we instantiate our basic NCE scheme (which is based on LWE) on top of ring LWE instead, we can shrink the public key size from $\tilde{\mathcal {O}}(k^2)$ to $\tilde{\mathcal {O}}(k)$. Finally, we remark that the hardness of ring LWE can be based on the worst-case hardness of lattice problems on ideal lattices.

Trapdoors for LWE. Micciancio and Peikert [MP12] show how to embed a trapdoor into a matrix $\mathbf {A}\in {\mathbb Z}_q^{m\times k}$ which allows solving several tasks which are usually believed to be hard. In their construction, the trapdoor of $\mathbf {A}$ is a matrix $\mathbf {T}\in \{0,1\}^{(k\log q)\times m}$ such that $\mathbf {TA}=\mathbf {G}$, where $\mathbf {G}\in {\mathbb Z}_q^{(k\log q)\times k}$ is the so-called “gadget matrix”. To be precise,  [MP12] shows (among other things) how to sample the pair $(\mathbf {A},\mathbf {T})$ in such a way so that (1) $\mathbf {A}$ is statistically close to uniform in ${\mathbb Z}_q^{m\times k}$ and (2) there is an efficient algorithm $\mathsf{Sample}_\sigma$ which takes as input the tuple $(\mathbf {u}, \mathbf {A}, \mathbf {T})$ where $\mathbf {u}\in {\mathbb Z}_q^k$ is arbitrary and outputs a vector $\mathbf {r}\in {\mathbb Z}_q^m$ from a distribution which is statistically close to $D_{\sigma ,\mathbf {u},\mathbf {A}}$, the discrete Gaussian of standard deviation $\sigma$ on the lattice

$$\begin{aligned} \varLambda _{\mathbf {u}}(\mathbf {A})=\{\mathbf {v} \in {\mathbb Z}_q^m:\mathbf {v}^\mathsf{t}\mathbf {A}=\mathbf {u}^\mathsf{t}\}. \end{aligned}$$

Their construction carries over to the ring setting as well.

2.4 Error Correcting Codes

Our construction makes use of constant-rate binary codes which are uniquely and efficiently decodeable from a $\bigl (1/2-\delta \bigr )-$fraction of computationally bounded errors. Such codes are constructed in [MPSW05] by using efficient list-decodeable codes along with computationally secure signatures. We will further assume that our codes are balanced, in the sense that exactly half of the bits of all codewords are 0 s and the other half are 1s. This can be arranged, for example, by concatenating a list decodeable code with a suitable binary error correcting code.

2.5 The Binomial and Hypergeometric Distributions

Binomial Distribution. A binomial random variable $X_{p,n}$ is equal to the number of successes when an experiment with success probability p is independently repeated n times. The density function is given by $\text {Pr}_{}(X_{p,n}=k)=\left( {\begin{array}{c}n\\ k\end{array}}\right) p^k(1-p)^{n-k}$ with expectation $\mathbb {E}\bigl [X_{p,n}\bigr ]=pn$. We denote the binomial distribution by $\mathsf{B}_p(n)$.

Hypergeometric Distribution. Our construction involves the randomized process: given $a,b<n$ independently choose random subsets $A,B\subset \{1,\dots ,n\}$ of sizes a and b. We will be interested in the size of the intersection $A\cap B$, which defines a hypergeometric random variable $X_{a,b,n}$ with density function $\text {Pr}_{}(X_{a,b,n}=k)=\left( {\begin{array}{c}b\\ k\end{array}}\right) \left( {\begin{array}{c}n-b\\ a-k\end{array}}\right) \big /\left( {\begin{array}{c}n\\ a\end{array}}\right)$ and expectation $\mathbb {E}\bigl [X_{a,b,n}\bigr ]=ab/n$. We denote the hypergeometric distribution of $X_{a,b,n}$ by $\mathsf{H}(a,b,n)$.

Multivariate Hypergeometric Distribution. We will also use a variant of the above process when $\{1,\dots ,n\}$ has been partitioned $\{1,\dots ,n\}=B_1\cup \cdots \cup B_t$ where $|B_i|=b_i$. Then if $A\subset \{1,\dots ,n\}$ of size a is chosen randomly, independent of the partition, the tuple $\bigl (|A\cap B_1|,\dots ,|A\cap B_t|\bigr )$ is a multivariate hypergeometric random variable $X_{a,\{b_i\},n}$ with density function

$$\begin{aligned} \text {Pr}_{}\bigl (X_{a,\{b_i\},n}=(k_1,\dots ,k_t)\bigr )=\frac{\left( {\begin{array}{c}b_1\\ k_1\end{array}}\right) \cdots \left( {\begin{array}{c}b_t\\ k_t\end{array}}\right) }{\left( {\begin{array}{c}n\\ a\end{array}}\right) }, \end{aligned}$$

where $k_1+\cdots + k_t=a$. The expectation is $\bigl (ab_1/n,\dots ,ab_t/n\bigr )$. We denote the multivariate hypergeometric distribution $\mathsf{H}^t\bigl (a,\{b_1,\dots ,b_t\},n\bigr )$. Note that the single variable hypergeometric distribution $\mathsf{H}(a,b,n)$ is the same as $\mathsf{H}^2\bigl (a,\{b,n-b\},n\bigr )$ corresponding to the partition $\{1,\dots ,n\}=B\cup \overline{B}$. We will make use of the following tail bounds on $\mathsf{B}_p(n)$, $\mathsf{H}(a,b,n)$ and $\mathsf{H}^t\bigl (a,\{b_i\},n\bigr )$ proved by Hoeffding [Hoe63].

Lemma 1

(Tail Bounds). Let $\alpha ,\beta ,\epsilon \in (0,1)$ be constants. Also for a constant t, choose constants $\beta _1,\dots ,\beta _t\in (0,1)$ such that $\beta _1+\cdots +\beta _t=1$. Set $a=\alpha n$, $b=\beta n$ and $b_i=\beta _in$.

• 1. Let X be a random variable drawn either from $\mathsf{B}_{\alpha \beta }(n)$ or $\mathsf{H}(a,b,n)$. Then

  $$\begin{aligned} \text {Pr}_{}\bigl (X\ge (\alpha \beta +\epsilon )n\text { OR }X\le (\alpha \beta -\epsilon )n\bigr )=e^{-\varOmega (n)} \end{aligned}$$

• 2. Let $(X_1,\dots ,X_t)$ be a random variable drawn from $\mathsf{H}^t\bigl (a,\{b_1,\dots ,b_t\},n\bigr )$. Then

  $$\begin{aligned} \text {Pr}_{}\bigl (\exists \text { }i\text { st }X_i\ge (\alpha \beta _i+\epsilon )n\text { OR }X_i\le (\alpha \beta _i-\epsilon )n\bigr )=e^{-\varOmega (n)}. \end{aligned}$$

The constants hidden by $\varOmega$ depend quadratically on $\epsilon$.

3 Non-Committing Encryption from LWE

3.1 The Basic Scheme

Params. Our scheme involves the following parameters:

• integers k, n, q and $m>2k\log q$;

• real numbers $\sigma ,\sigma '$ such that $2\sqrt{k}<\sigma <\sigma '<q/\sqrt{k}$ and such that $\sigma ^2/\sigma '=\mathsf{negl}(k)$;

• integers $c_R,c_S\le n$ and $\delta \in (0,1)$ such that $\delta <c_Rc_S/2n^2$. To be concrete, we set $c_R=c_S=n/8$.

KeyGen. Draw and let $I_R\subset \{1,\dots ,n\}$ be a random subset of size $c_R$. Define vectors $\mathbf {v}_i\in {\mathbb Z}_q^m$ for $i=1,\dots ,n$:

$$\begin{aligned} \mathbf {v}_i=\left\{ \begin{array}{lr} \mathbf {A}\mathbf {s}_i+\mathbf {e}_i, &{} i\in I_R\\ \text {uniform in } {\mathbb Z}_q^m, &{} i\notin I_R\end{array}\right. \end{aligned}$$

where and . Output $(\mathsf{pk},\mathsf{sk})=\bigl ((\mathbf {A},\mathbf {v}_1,\dots ,\mathbf {v}_n);\{\mathbf {s}_i\}_{i\in I_R}\bigr )$.

Encryption. Given $\mathsf{msg}\in \{0,1\}^\ell$ and $\mathsf{pk}=(\mathbf {A},\mathbf {v}_1,\dots ,\mathbf {v}_n)$, let $y=(y_1,\dots ,y_n)=\mathbf {ECC}(\mathsf{msg})\in \{0,1\}^n$ where $\mathbf {ECC}$ is a balanced binary error-correcting code with constant rate, which is uniquely decodeable from a $\bigl (1/2-\delta \bigr )-$fraction of computationally bounded errors, as described in Sect. 2.3. Choose a random subset $I_S\subset \{1,\dots ,n\}$ of size $c_S$. Also, for each $i\notin I_S$, choose a random bit $z_i\leftarrow \{0,1\}$. Finally, choose $\mathbf {r}\leftarrow \chi _\sigma ^m$ and $e_1',\dots ,e_n'\leftarrow \chi _{\sigma '}$. Output ciphertext $\mathsf{ct}=(\mathbf {u},w_1,\dots ,w_n)$ where $\mathbf {u}^\mathsf{t}=\mathbf {r}^\mathsf{t}\mathbf {A}\in {\mathbb Z}_q^{1\times k}$, and $w_i\in {\mathbb Z}_q$ is given by

$$\begin{aligned} w_i=\left\{ \begin{array}{lr} \mathbf {r}^\mathsf{t}\mathbf {v}_i+e'_i+(q/2)y_i, &{} i\in I_S\\ \mathbf {r}^\mathsf{t}\mathbf {v}_i+e_i'+(q/2)z_i, &{} i\notin I_S\end{array}\right. . \end{aligned}$$

The encryption randomness is $\bigl (I_S,\{z_i\}_{i\notin I_S},\mathbf {r},e_1',\dots ,e_n'\bigr )$.

Decryption. Given $\mathsf{ct}=(\mathbf {u},w_1,\dots ,w_n)$ and $\mathsf{sk}=\{\mathbf {s}_i\}_{i\in I_R}$, set

$$\begin{aligned} y_i'=\left\lfloor \frac{2(w_i-\mathbf {u}^\mathsf{t}\mathbf {s}_i)}{q} \right\rceil \end{aligned}$$

for all $i\in I_R$, and extend to a string $y'\in \{0,1\}^n$ via when $i\notin I_R$. Output $\mathsf{msg}'\in \{0,1\}^\ell$ obtained by applying the decoding algorithm of $\mathbf {ECC}$ to $y'$.

3.2 Correctness and Real World Subsets

Correctness. Let $y'=(y_1',\dots ,y_n')\in \{0,1\}^n$ be the faulty codeword obtained during decryption. We must show that the decoding algorithm correctly outputs $\mathsf{msg}$ with overwhelming probability. We have:

• $\underline{i\in I_R\cap I_S:}$ then $y_i'=y_i$. The number of such i is $k\leftarrow \mathsf{H}(c_R,c_S,n)$.

• $\underline{i\notin I_R\cap I_S:}$ then $y_i'=y_i$ with probability 1 / 2 independently of all other i.

It follows that the codeword $y'$ has $k'$ errors and $n-k'$ correct symbols where $k'\leftarrow \mathsf{B}_{1/2}(n-k)$. Fix a constant $\epsilon >0$ with $3\epsilon <c_Rc_S/n^2-2\delta$. We have, by Lemma 1, that with all but negligible probability in n,

$$\begin{aligned} k'\le (1/2+\epsilon )(n-k)\le n(1/2+\epsilon )(1+\epsilon -c_Rc_S/n^2)\le n(1/2-\delta ). \end{aligned}$$

In this case, the fraction of errors in the faulty codeword $y'$ is less than $1/2-\delta$ and so $y'$ decodes correctly and decryption succeeds.

Efficiency. The ciphertext size of our scheme is $(n+k)\log q=\mathcal {O}\bigl (n\text {polylog}(k)\bigr )$, while the public key is of size $m(k+n)\log q=\mathcal {O}\bigl (k^2\text {polylog}(k)\bigr )$. We remark that when this construction is instantiated using a ring-LWE based encryption scheme as described in [LPR13], the public key size can be reduced to $\mathcal {O}\bigl (k\text {polylog}(k)\bigr )$. This requires using the ring based version of the trapdoors from [MP12].

Real World Subsets. The most technically delicate issue with our construction is that the faulty codeword $y'$ produced in simulation must have the same distribution of errors as in the real world. In particular, the adversary learns four sets

• $\underline{\mathsf{ECC}_0:}$ The set of coordinates where the codeword is 0.

• $\underline{I_S:}$ The set of coordinates “honestly” generated by the sender.

• $\underline{D_0:}$ The set of coordinates outside of $I_S$ that “randomly” encrypt a 0.

• $\underline{I_R:}$ The set of coordinates where the receiver has the decryption key.

These sets also define their complements, $\overline{\mathsf{ECC}_0} = \mathsf{ECC}_1$ is the set of coordinates where the codeword is one, and $D_1$ is the set of coordinates that were random encryptions of a one, thus $D_0 \cap D_1 = \overline{I_S}$. Note that $\mathsf{ECC}_0$ and $\mathsf{ECC}_1$ are defined by the message, $I_S$, $D_0$ and $D_1$ are defined by the sender’s randomness and $I_R$ is defined by the receiver’s randomness. Therefore, in an honest execution, the sets $I_S,D_0,D_1$ will be independent of $\mathsf{ECC}_0$, and $I_R$ will be independent of everything. We let $\mathsf{F}_\mathsf{real}$ be the resulting distribution on $(I_R,I_S,D_0,D_1)$. So whenever $|I_R|=c_R$, $|I_S|=c_S$ and $\{1,\dots ,n\}=I_S\cup D_0\cup D_1$ is a partition, the probability density function is given by

$$\begin{aligned} \text {Pr}\bigl (\mathsf{F}_\mathsf{real}=(I_R,I_S,D_0,D_1)\bigr )=\frac{1}{2^n \left( {\begin{array}{c}n\\ c_R\end{array}}\right) \left( {\begin{array}{c}n\\ c_S\end{array}}\right) }. \end{aligned}$$

Even though $\mathsf{F}_\mathsf{real}$ is independent of $\mathsf{msg}$, we often write $(I_R,I_S,D_0,D_1)\leftarrow \mathsf{F}_\mathsf{real}(\mathsf{msg})$ when we are interested in how the sets intersect $\mathsf{ECC}_0$ and $\mathsf{ECC}_1$, defined by $\mathsf{msg}$. The three different partitions

$$\begin{aligned} \{1,\dots ,n\} = \mathsf{ECC}_0 \cup \mathsf{ECC}_1 = I_S \cup D_0 \cup D_1 = I_R \cup \overline{I_R}, \end{aligned}$$

let us further partition $\{1,\dots ,n\}$ into 12 subsets by choosing one set from each partition. We compute now the sizes of the various intersections as this information will be important in defining our simulator.

As the error correcting code is balanced, we have $|\mathsf{ECC}_0| = |\mathsf{ECC}_1| = \frac{n}{2}$. We have, therefore, that $|I_S\cap \mathsf{ECC}_0|=k\leftarrow \mathsf{H}\bigl (c_S,\frac{n}{2},n\bigr )$, and $|I_S\cap \mathsf{ECC}_1|=c_S-k$. Similarly, $|D_0\cap \mathsf{ECC}_0|=k'\leftarrow \mathsf{B}_{1/2}\bigl (\frac{n}{2}-k\bigr )$ and $|D_0\cap \mathsf{ECC}_1|=k''\leftarrow \mathsf{B}_{1/2}\bigl (\frac{n}{2}-c_S+k\bigr )$ which fixes $|D_1\cap \mathsf{ECC}_0|=\frac{n}{2}-k-k'$ and $|D_1\cap \mathsf{ECC}_1|=\frac{n}{2}-c_S+k-k''$. As $I_R$ is chosen independently to be a random subset of $\{1,\dots ,n\}$ of size $c_R$, if we set

$$\begin{aligned} \alpha _b=|I_R\cap I_S\cap \mathsf{ECC}_b|;\text { }\beta _b=|I_R\cap D_0\cap \mathsf{ECC}_b|;\text { }\gamma _b=|I_R\cap D_1\cap \mathsf{ECC}_b|, \end{aligned}$$

(thus fixing $|\overline{I_R}\cap I_S\cap \mathsf{ECC}_0|=k-\alpha _0$ and so on), then

$$(\alpha _0,\beta _0,\gamma _0,\alpha _1,\beta _1,\gamma _1) \longleftarrow \mathsf{H}^6\biggl (c_R,\Big \{k,k',\frac{n}{2}-k-k', c_S-k,k'',\frac{n}{2}-c_S+k-k'' \Big \},n\biggr ).$$

This calculation will be useful when building our simulator.

3.3 The Simulator

Simulated Public Key and Ciphertext. Fix $c_\mathsf{good}=3n/4$. The simulator chooses $\hat{\mathbf {A}}\in {\mathbb Z}_q^{m\times (k+n-c_\mathsf{good})}$ along with a trapdoor $\mathbf {T}\in \{0,1\}^{n\log q\times m}$ such that $\mathbf {T}\hat{\mathbf {A}}=\mathbf {G}$ according to [MP12]. He picks a random subset $I_\mathsf{good}\subset \{1,\dots ,n\}$ of size $c_\mathsf{good}$, and sets $I_\mathsf{bad}=\{1,\dots ,n\}-I_\mathsf{good}$. Write $\hat{\mathbf {A}}=\bigl [\mathbf {A}\big |\mathbf {V}\bigr ]$ where $\mathbf {A}\in {\mathbb Z}_q^{m\times k}$ and $\mathbf {V}\in {\mathbb Z}_q^{m\times (n-c_\mathsf{good})}$. For $i\in I_\mathsf{good}$, draw $\mathbf {s}_i\leftarrow {\mathbb Z}_q^k$ and $\mathbf {e}_i\leftarrow \chi _\sigma ^m$ and define $\mathbf {v}_1,\dots ,\mathbf {v}_n\in {\mathbb Z}_q^m$:

$$\begin{aligned} \mathbf {v}_i=\left\{ \begin{array}{ll} \mathbf {A}\mathbf {s}_i+\mathbf {e}_i, &{} i\in I_\mathsf{good}\\ \text {column of }\mathbf {V}, &{} i\in I_\mathsf{bad}\end{array}\right. , \end{aligned}$$

so that the vectors $\{\mathbf {v}_i\}_{i\in I_\mathsf{bad}}$ are the columns of $\mathbf {V}$. The public key is $\mathsf{pk}=(\mathbf {A},\mathbf {v}_1,\dots ,\mathbf {v}_n)$ and the data $\{\mathbf {s}_i\}_{i\in I_\mathsf{good}}$ is stored as it will be used when generating the secret key: $I_R$ will be a proper subset of $I_\mathsf{good}$.

The simulater then chooses , for $i\in I_\mathsf{good}$, and randomly partitions $I_\mathsf{good}$ into subsets of equal size $I_{\mathsf{good},0}$ and $I_{\mathsf{good},1}$. The ciphertext is $\mathsf{ct}=(\mathbf {u},w_1,\dots ,w_n)$ where $\mathbf {u}^\mathsf{t}=\mathbf {r}^\mathsf{t}\mathbf {A}\in {\mathbb Z}_q^{1\times k}$ and

The subsets $I_{\mathsf{good},0},I_{\mathsf{good},1},I_\mathsf{bad}$ are stored for use when generating the encryption randomness.

Simulated Secret Key and Randomness. $\mathcal {S}$ draws $(I_R,I_S,D_0,D_1)\leftarrow \mathsf{F}_\mathsf{ideal}(\mathsf{msg},I_{\mathsf{good},0},I_{\mathsf{good},1})$, where the ideal world subset function $\mathsf{F}_\mathsf{ideal}$ is defined below (so in particular, $|I_R|=c_R$, $|I_S|=c_S$ and $I_S,D_0,D_1$ is a partition of $\{1,\dots ,n\}$). The simulator then sets the secret key to $\{\mathbf {s}_i\}_{i\in I_R}$ using the vectors $\{\mathbf {s}_i\}_{i\in I_\mathsf{good}}$ computed during public key generation. To compute the randomness, $\mathcal {S}$ sets $z_i=b$ for all $i\in D_b$. Then for each $i\in I_\mathsf{bad}$, it draws $e_i'\leftarrow \chi _{\sigma '}$ and uses the trapdoor $\mathbf {T}$ to sample a Gaussian $\overline{\mathbf {r}}\in {\mathbb Z}_q^m$ such that $\overline{\mathbf {r}}^\mathsf{t}\mathbf {A}=\mathbf {u}$ and $\overline{\mathbf {r}}^\mathsf{t}\mathbf {v}_i=w_i-e_i'-(q/2)z_i$ for all $i\in I_\mathsf{bad}$. Finally, for $i\in I_\mathsf{good}$, $\mathcal {S}$ sets $e_i'=e_i^*+(\mathbf {r}-\overline{\mathbf {r}})^\mathsf{t}e_i$ and defines the encryption randomness $\mathsf{rand}=\bigl (I_S,\{z_i\}_{i\notin I_S},\overline{\mathbf {r}},e_1',\dots ,e_n'\bigr )$.

Ideal World Subsets. We now describe the distribution $\mathsf{F}_\mathsf{ideal}$ which the simulator chooses to define the sets $I_R$, $I_S$, $D_0$, $D_1$. For simplicity, we assume that the target message $\mathsf{msg}$ is given at the beginning before all random choices are made. This is not exactly what happens in the ideal world, where the non-committing adversary $\mathcal {A}$ gets to see $\mathsf{pk}$ before specifying $\mathsf{msg}$. However, it follows directly from the hardness of LWE that $\mathcal {A}$ cannot gain advantage by specifying $\mathsf{msg}$ after seeing $\mathsf{pk}$.

Upon receiving $\mathsf{msg}\in \{0,1\}^\ell$ as input, $\mathsf{F}_\mathsf{ideal}$ sets $y=(y_1,\dots ,y_n)=\mathbf {ECC}(\mathsf{msg})\in \{0,1\}^n$ to be the target codeword, defining $\mathsf{ECC}_0=\{i:y_i=0\}$ and $\mathsf{ECC}_1=\{i:y_i=1\}$. It then chooses a random $I_\mathsf{good}\subset \{1,\dots ,n\}$ of size $c_\mathsf{good}$ and $I_\mathsf{bad}=\{1,\dots ,n\}-I_\mathsf{good}$ as in the real world. It further divides $I_\mathsf{good}$ randomly into two halves $I_{\mathsf{good},0}$ and $I_{\mathsf{good},1}$ defining two partitions

$$\begin{aligned} \{1,\dots ,n\} =\mathsf{ECC}_0\cup \mathsf{ECC}_1=I_{\mathsf{good},0}\cup I_{\mathsf{good},1}\cup I_\mathsf{bad}. \end{aligned}$$

The resulting six intersections have sizes:

• $|I_{\mathsf{good},0}\cap \mathsf{ECC}_0|=t\leftarrow \mathsf{H}\bigl ( \frac{n}{2},\frac{c_\mathsf{good}}{2},n\bigr )$; $|I_{\mathsf{good},0}\cap \mathsf{ECC}_1|=\frac{c_\mathsf{good}}{2}-t$;

• $|I_{\mathsf{good},1}\cap \mathsf{ECC}_0|=t'\leftarrow \mathsf{H}\bigl ( \frac{n}{2}-t,\frac{c_\mathsf{good}}{2},n-\frac{c_\mathsf{good}}{2}\bigr )$; $|I_{\mathsf{good},1}\cap \mathsf{ECC}_1|=\frac{c_\mathsf{good}}{2}-t'$;

• $|I_\mathsf{bad}\cap \mathsf{ECC}_0|=\frac{n}{2}-t-t'$; $|I_\mathsf{bad}\cap \mathsf{ECC}_1|=\frac{n}{2}-c_\mathsf{good}+t+t'$.

$\mathsf{F}_\mathsf{ideal}$ needs to output $I_R,I_S,D_0,D_1\subset \{1,\dots ,n\}$ such that the various intersections have the same sizes as in the real world. It proceeds as follows:

• 1. $\mathsf{F}_\mathsf{ideal}$ draws random variables $k\leftarrow \mathsf{H}\bigl (c_S,\frac{n}{2},n\bigr )$, $k'\leftarrow \mathsf{B}_{1/2}\bigl (\frac{n}{2}-k\bigr )$, $k''\leftarrow \mathsf{B}_{1/2}\bigl (\frac{n}{2}-c_S+k\bigr )$ and $(\alpha _0,\beta _0,\gamma _0, \alpha _1,\beta _1, \gamma _1)\leftarrow \mathsf{H}^6\bigl (c_R,\{k,k',\frac{n}{2}-k-k', c_S-k,k'',\frac{n}{2}-c_S+k-k''\},n\bigr )$.

• 2. $\mathsf{F}_\mathsf{ideal}$ defines:

  • $\underline{I_R\cap I_S\cap \mathsf{ECC}_b:}$ a random subset of $I_{\mathsf{good},b}\cap \mathsf{ECC}_b$ of size $\alpha _b$;

  • $\underline{I_R\cap D_0\cap \mathsf{ECC}_b:}$ a random subset of $I_{\mathsf{good},0}\cap \mathsf{ECC}_b$ of size $\beta _b$;

  • $\underline{I_R\cap D_1\cap \mathsf{ECC}_b:}$ a random subset of $I_{\mathsf{good},1}\cap \mathsf{ECC}_b$ of size $\gamma _b$;

  in such a way so that all six sets are disjoint. We prove in Claim 3.3 that the subsets $I_{\mathsf{good},b}\cap \mathsf{ECC}_{b'}$ are large enough to allow the above definitions with high probability. This fully defines $I_R$, but not $I_S$, $D_0$, $D_1$ (we still need their intersections with $\overline{I_R}$). Let $\mathsf{Rem}_b\subset I_{\mathsf{good},b}$ be the $i\in I_{\mathsf{good},b}$ that remain unassigned after this process.

  Remark: As $I_R$ is now fully defined, we will not need the secret keys for the $i\in \mathsf{Rem}_0\cup \mathsf{Rem}_1$. The only difference moving forward between $\mathsf{Rem}_0$, $\mathsf{Rem}_1$ and $I_\mathsf{bad}$ is that the ciphertexts $v_i$ for $i\in \mathsf{Rem}_b$ can only be decrypted to b, whereas the ciphertexts $v_i$ for $i\in I_\mathsf{bad}$ can be decrypted to 0 or 1 as they were generated with lossy public keys.

• 3. The sizes computed so far, along with the requirements $|I_S| = c_S$, $|I_S \cap \mathsf{ECC}_0| = k$, $|D_0\cap \mathsf{ECC}_0| = k'$, and $|D_0\cap \mathsf{ECC}_1| = k''$ determine the sizes of the remaining six sets. For example,

  $$\begin{aligned} |\overline{I_R}\cap I_S\cap \mathsf{ECC}_0|=|I_S\cap \mathsf{ECC}_0|-|I_R \cap I_S\cap \mathsf{ECC}_0|=k-\alpha _0. \end{aligned}$$

  $\mathsf{F}_\mathsf{ideal}$ sets

  • $\underline{\overline{I_R}\cap I_S\cap \mathsf{ECC}_b:}$ subset of $(\mathsf{Rem}_b\cup I_\mathsf{bad})\cap \mathsf{ECC}_b$;

  • $\underline{\overline{I_R}\cap D_0\cap \mathsf{ECC}_b:}$ subset of $(\mathsf{Rem}_0\cup I_\mathsf{bad})\cap \mathsf{ECC}_b$;

  • $\underline{\overline{I_R}\cap D_1\cap \mathsf{ECC}_b:}$ subset of $(\mathsf{Rem}_1\cup I_\mathsf{bad})\cap \mathsf{ECC}_b$;

  randomly such that (1) all six sets are disjoint and of the required size, (2) $\mathsf{Rem}_b\cap \mathsf{ECC}_b$ is fully contained in $\overline{I_R}\cap (I_S\cup D_b)\cap \mathsf{ECC}_b$, $\mathsf{Rem}_b\cap \mathsf{ECC}_{1-b}$ is fully contained in $\overline{I_R}\cap D_b\cap \mathsf{ECC}_{1-b}$. We prove in Claim 3.3 below that this is possible whp.

• 4. $\mathsf{F}_\mathsf{ideal}$ outputs $(I_R,I_S,D_0,D_1)$.

Claim

If we set $c_\mathsf{good}=3n/4$, $c_R=c_S=n/8$ then whp over the choice of $I_{\mathsf{good},0}$, $I_{\mathsf{good},1}$ and the random variables drawn in step 1, it is possible to define the subsets in steps 2 and 3 above.

Proof

Step 2 requires

$$\begin{aligned} (I_R\cap (I_S\cup D_b)\cap \mathsf{ECC}_b)\subset I_{\mathsf{good},b}\cap \mathsf{ECC}_b;\text { }(I_R\cap D_{1-b}\cap \mathsf{ECC}_b)\subset I_{\mathsf{good},1-b}\cap \mathsf{ECC}_b \end{aligned}$$

for $b=0,1$ which is possible if and only if the four inequalities are satisfied:

$$\begin{aligned} \alpha _0+\beta _0\le t;\text { }\alpha _1+\gamma _1\le \frac{c_\mathsf{good}}{2}-t';\text { }\gamma _0\le t';\text { }\beta _1\le \frac{c_\mathsf{good}}{2}-t. \end{aligned}$$

To see that all four are satisfied with high probability, note that the expectation of each right side is $c_\mathsf{good}/4$, while the largest expectation of a left side is $c_R+3c_Rc_S/2n$.

On the other hand, step 3 requires

$$\begin{aligned} \mathsf{Rem}_b\cap \mathsf{ECC}_b\subset \overline{I_R}\cap (I_S\cup D_b)\cap \mathsf{ECC}_b;\text { }\mathsf{Rem}_{1-b}\cap \mathsf{ECC}_b\subset \overline{I_R}\cap D_{1-b}\cap \mathsf{ECC}_b, \end{aligned}$$

for $b=0,1$, which is possible if and only if the four inequalities are satisfied:

$$\begin{aligned} t\le k+k';\text { }\frac{c_\mathsf{good}}{2}-t'\le \frac{n}{2}-k'';\text { }t'\le \frac{n}{2}-k-k';\text { }\frac{c_\mathsf{good}}{2}-t\le k''. \end{aligned}$$

The expectations of all four left hand sides is $c_\mathsf{good}/4$, while the smallest right hand side has expectation $(n-c_S)/4$. If we set $\epsilon =1/64$ then $c_\mathsf{good}=3n/4$, $c_R=c_S=n/8$ satisfy

$$\begin{aligned} c_R+\frac{3c_Rc_S}{2n}+\epsilon n<\frac{c_\mathsf{good}}{4}<\frac{n-c_S}{4}-\epsilon n, \end{aligned}$$

and so the tail bound in Lemma 1, implies that all of the inequalities are satisfied with high probability.

We note that while $\epsilon =1/64$ might be unsatisfactory in practice since the confidence offered by Lemma 1 is $1-\exp \bigl (-\epsilon ^2n/2\bigr )$ (recall n is the message length which is a large constant times the security parameter, so $\epsilon =1/64$ might well be fine), different values of $\epsilon$ may be obtained by varying $c_R$, $c_S$, and $c_\mathsf{good}$.      $\square$

Claim

The subsets $I_R,I_S,D_0,D_1$ output by the above process are distributed within negligible statistical distance of the corresponding subsets which arise in the real world, with high probability.

Proof

We compute the probability that the tuple $(I_R,I_S,D_0,D_1)$ is output in the ideal worlds and check that it equals

$$\begin{aligned} \frac{1}{2^n\left( {\begin{array}{c}n\\ c_R\end{array}}\right) \left( {\begin{array}{c}n\\ c_S\end{array}}\right) }, \end{aligned}$$

like in the real world. We make two observations. Note first that for any $\mathsf{msg}\in \{0,1\}^\ell$ which defines $\mathsf{ECC}_0$ and $\mathsf{ECC}_1$, a process which outputs $(I_R,I_S,D_0,D_1)$ can be equivalently thought of as a process which outputs 12 pairwise disjoint subsets corresponding to the twelve intersections of the three partitions

$$\begin{aligned} \{1,\dots ,n\}=\mathsf{ECC}_0\cup \mathsf{ECC}_1=I_S\cup D_0\cup D_1=I_R\cup \overline{I_R}. \end{aligned}$$

The second observation is that choosing a random subset $A\subset \{1,\dots ,n\}$ of size a and then outputting a random subset $B\subset A$ of size b is the same as just outputting a random subset of $\{1,\dots ,n\}$ of size b. With these observations in mind, it is not difficult to complete the computation that

$$\begin{aligned} \text {Pr}_\mathsf{ideal}(I_R,I_S,D_0,D_1)=\frac{1}{2^n\left( {\begin{array}{c}n\\ c_R\end{array}}\right) \left( {\begin{array}{c}n\\ c_S\end{array}}\right) }, \end{aligned}$$

for any $\mathsf{msg}\in \{0,1\}^\ell$. The details are left to the reader.      $\square$

3.4 Proof of Security

$H_0$ $-$ The Ideal World.

• $\mathcal {C}$ chooses a random $I_\mathsf{good}\subset \{1,\dots ,n\}$ of size $c_\mathsf{good}$ and $\hat{\mathbf {A}}=\bigl [\mathbf {A}|\mathbf {V}\bigr ]\in {\mathbb Z}_q^{m \times (k+n-c_\mathsf{good})}$ along with a trapdoor $\mathbf {T}\in \{0,1\}^{n\log q\times m}$ such that $\mathbf {T}\hat{\mathbf {A}}=\mathbf {G}$ according to [MP12]. Then for each $i\in I_\mathsf{good}$, $\mathcal {C}$ draws $\mathbf {s}_i\leftarrow {\mathbb Z}_q^n$ and $\mathbf {e}_i\leftarrow \chi _\sigma ^m$ and sets $\mathbf {v}_i=\mathbf {As}_i+\mathbf {e}_i$. For $i\in I_\mathsf{bad}$ $\mathcal {C}$ lets $\mathbf {v}_i$ be a column of $\mathbf {V}$. $\mathcal {C}$ sets $\mathsf{pk}=(\mathbf {A},\mathbf {v}_1,\dots ,\mathbf {v}_n)$ and saves $\{\mathbf {s}_i\}_{i\in I_\mathsf{good}}$.

• $\mathcal {C}$ randomly partitions $I_\mathsf{good}$ into two halves of equal sizes $I_{\mathsf{good},0}$ and $I_{\mathsf{good},1}$ and chooses $\mathbf {r}\leftarrow \chi _\sigma ^m$, setting $\mathbf {u}^\mathsf{t}=\mathbf {r}^\mathsf{t}\mathbf {A}\in {\mathbb Z}_q^{1\times k}$. For $i\in I_{\mathsf{good},b}$, $\mathcal {C}$ sets $w_i=\mathbf {r}^\mathsf{t}\mathbf {v}_i+e_i^*+(q/2)b$ where each $e_i^*\leftarrow \chi _{\sigma '}$. For $i\in I_\mathsf{bad}$, $\mathcal {C}$ lets $w_i\in {\mathbb Z}_q$ be random. $\mathcal {C}$ sets $\mathsf{ct}=(\mathbf {u},w_1,\dots ,w_n)$.

• $\mathcal {C}$ sends $\mathsf{pk}$ to $\mathcal {A}$ and receives $\mathsf{msg}$.

• $\mathcal {C}$ computes $(I_R,I_S,D_0,D_1)\leftarrow \mathsf{F}_\mathsf{ideal}(\mathsf{msg},I_{\mathsf{good},0},I_{\mathsf{good},1})$ and sets $\mathsf{sk}=\bigl (I_R,\{\mathbf {s}_i\}_{i\in I_R}\bigr )$.

• Finally, for each $i\in I_\mathsf{bad}\cap D_b$, $\mathcal {C}$ draws $e_i'\leftarrow \chi _{\sigma '}$ and sets $w_i'=w_i-e_i'-(q/2)b$, then $\mathcal {C}$ draws $\overline{\mathbf {r}}\leftarrow \mathsf{Sample}_{\sigma }\bigl (\mathbf {u}',\hat{\mathbf {A}},\mathbf {T}\bigr )$ according to [MP12] where $\mathbf {u}'=\bigl (\mathbf {u},\{w_i'\}_{i\in I_\mathsf{bad}}\bigr )\in {\mathbb Z}_q^{k+n-c_\mathsf{good}}$. For each $i\in I_\mathsf{good}$, $\mathcal {C}$ sets $e_i'=e_i^*+(\mathbf {r}-\overline{\mathbf {r}})^\mathsf{t}\mathbf {e}_i$. Lastly, for each $i\in D_b$, $\mathcal {C}$ sets $z_i=b$. He collects all of this information into $\mathsf{rand}=\bigl (I_S,\{z_i\}_{i\notin I_S},\overline{\mathbf {r}},e_1',\dots ,e_n'\bigr )$.

• $\mathcal {C}$ sends $(\mathsf{ct},\mathsf{sk},\mathsf{rand})$.

$H_1$ $-$ The main difference between this world and $H_0$ is that here $\mathcal {C}$ does not choose $\mathsf{ct}$ until after he sends $\mathsf{pk}$ to $\mathcal {A}$ and receives $\mathsf{msg}$. This allows us to avoid selecting $\overline{\mathbf {r}}$ or the $e_i^*$.

• $\mathcal {C}$ chooses $I_\mathsf{good}\subset \{1,\dots ,n\}$, $\hat{\mathbf {A}}=\bigl [\mathbf {A}|\mathbf {V}\bigr ]\in {\mathbb Z}_q^{m \times (k+n-c_\mathsf{good})}$, $\{\mathbf {s}_i\}_{i\in I_\mathsf{good}}$ and $\{\mathbf {e}_i\}_{i\in I_\mathsf{good}}$ and $\{\mathbf {v}_i\}_{i=1,\dots ,n}$ just as in $H_0$ and sets $\mathsf{pk}=(\mathbf {A},\mathbf {v}_1,\dots ,\mathbf {v}_n)$, saving $\{\mathbf {s}_i\}_{i\in I_\mathsf{good}}$.

• $\mathcal {C}$ sends $\mathsf{pk}$ to $\mathcal {A}$ and receives $\mathsf{msg}$.

• $\mathcal {C}$ randomly chooses $I_{\mathsf{good},0}$ and $I_{\mathsf{good},1}$ and computes $(I_R,I_S,D_0,D_1)\leftarrow \mathsf{F}_\mathsf{ideal}(\mathsf{msg},I_{\mathsf{good},0},I_{\mathsf{good},1})$, and sets $\mathsf{sk}=\bigl (I_R,\{\mathbf {s}_i\}_{i\in I_R}\bigr )$.

• $\mathcal {C}$ chooses $\mathbf {r}\leftarrow \chi _\sigma ^m$ and for $i\in (I_S\cap I_{\mathsf{good},b})\cup D_b$, sets $z_i=b$ and $w_i=\mathbf {r}^\mathsf{t}\mathbf {v}_i+e_i'+(q/2)z_i$. $\mathcal {C}$ sets $\mathsf{ct}=(\mathbf {u},w_1,\dots ,w_n)$ and $\mathsf{rand}=(I_S,\{z_i\}_{i\notin I_S},\mathbf {r},e_1',\dots ,e_n')$.

• $\mathcal {C}$ sends $(\mathsf{ct},\mathsf{sk},\mathsf{rand})$.

Claim

$H_1\approx _\mathsf{s} H_0$.

Proof

We must show that the pair $\bigl (\overline{\mathbf {r}},\{e_i'\}_{i=1,\dots ,n}\bigr )\leftarrow H_0$ is statistically close to $\bigl (\mathbf {r},\{e_i'\}_i\bigr )\leftarrow H_1$. Note that $\overline{\mathbf {r}}$ is chosen by first drawing $\mathbf {r}\leftarrow \chi _\sigma ^m$ and then using the trapdoor preimage sampler to draw Gaussian $\overline{\mathbf {r}}$ such that $\overline{\mathbf {r}}^\mathsf{t}\hat{\mathbf {A}}=\mathbf {r}^\mathsf{t}\hat{\mathbf {A}}$. The induced distribution on $\overline{\mathbf {r}}$ is statistically close to simply drawing $\mathbf {r}\leftarrow \chi _\sigma ^m$ as in $H_1$. Second note that $e_i'\leftarrow \chi _{\sigma '}$ for all i in $H_1$, while in $H_0$, this is only the case for $i\in I_\mathsf{bad}$. For $i\in I_\mathsf{good}$, $e_i'=e_i^*+(\mathbf {r}-\overline{\mathbf {r}})^\mathsf{t}\mathbf {e_i}$ where $e_i^*\leftarrow \chi _{\sigma '}$ and $\mathbf {e_i}\leftarrow \chi _\sigma ^m$. This is statistically close to $\chi _{\sigma '}$ as $\sigma ^2/\sigma '=\mathsf{negl}(k)$, using Fact 1.      $\square$

$H_2$ $-$ In this world we draw $\mathbf {A}\in {\mathbb Z}_q^{m\times k}$ and $\{\mathbf {v}_i\}_{i\in I_\mathsf{bad}}$ randomly instead of along with a trapdoor.

• $\mathcal {C}$ chooses $I_\mathsf{good}\subset \{1,\dots ,n\}$, $\mathbf {A}\in {\mathbb Z}_q^{m \times k}$, and sets $\mathbf {v}_i=\mathbf {As}_i+\mathbf {e}_i$ for $i\in I_\mathsf{good}$ and $\mathbf {v}\leftarrow {\mathbb Z}_q^m$ for $i\in I_\mathsf{bad}$, where $\{\mathbf {s}_i\}_{i\in I_\mathsf{good}}$ and $\{\mathbf {e}_i\}_{i\in I_\mathsf{good}}$ are as in $H_1$. $\mathcal {C}$ sets $\mathsf{pk}=(\mathbf {A},\mathbf {v}_1,\dots ,\mathbf {v}_n)$, and saves $\{\mathbf {s}_i\}_{i\in I_\mathsf{good}}$.

• $\mathcal {C}$ sends $\mathsf{pk}$ to $\mathcal {A}$ and receives $\mathsf{msg}$.

• $\mathcal {C}$ randomly chooses $I_{\mathsf{good},0}$ and $I_{\mathsf{good},1}$ and computes $(I_R,I_S,D_0,D_1)\leftarrow \mathsf{F}_\mathsf{ideal}(\mathsf{msg},I_{\mathsf{good},0},I_{\mathsf{good},1})$, and sets $\mathsf{sk}=\bigl (I_R,\{\mathbf {s}_i\}_{i\in I_R}\bigr )$.

• $\mathcal {C}$ chooses $\mathbf {r}\leftarrow \chi _\sigma ^m$ and for $i\in (I_S\cap I_{\mathsf{good},b})\cup D_b$, sets $z_i=b$ and $w_i=\mathbf {r}^\mathsf{t}\mathbf {v}_i+e_i'+(q/2)z_i$. $\mathcal {C}$ sets $\mathsf{ct}=(\mathbf {u},w_1,\dots ,w_n)$ and $\mathsf{rand}=(I_S,\{z_i\}_{i\notin I_S},\mathbf {r},e_1',\dots ,e_n')$.

• $\mathcal {C}$ sends $(\mathsf{ct},\mathsf{sk},\mathsf{rand})$.

Claim

$H_2\approx _\mathsf{s} H_1$.

Proof

This follows immediately from the fact that matrices drawn along with their trapdoors as in [MP12] are statistically close to uniform. As we weren’t using the trapdoor in $H_1$ anyway, changing $\hat{\mathbf {A}}$ to a uniform matrix, this does not affect anything functionally.      $\square$

$H_3$ $-$ The Real World. In this world we change the way the subsets $(I_R,I_S,D_0,D_1)$ are drawn; we draw them from $\mathsf{F}_\mathsf{real}$ instead of $\mathsf{F}_\mathsf{ideal}$.

• $\mathcal {C}$ draws $(I_R,I_S,D_0,D_1)\leftarrow \mathsf{F}_\mathsf{real}$ and a random $\mathbf {A}\in {\mathbb Z}_q^{m\times k}$ and sets $\mathbf {v}_i=\mathbf {As}_i+\mathbf {e}_i$ for $i\in I_R$ and $\mathbf {v}\leftarrow {\mathbb Z}_q^m$ for $i\notin I_R$, where $\{\mathbf {s}_i\}_{i\in I_R}$ and $\{\mathbf {e}_i\}_{i\in I_R}$ are as in $H_2$. $\mathcal {C}$ sets $\mathsf{pk}=(\mathbf {A},\mathbf {v}_1,\dots ,\mathbf {v}_n)$, and $\mathsf{sk}=\{\mathbf {s}_i\}_{i\in I_R}$.

• $\mathcal {C}$ sends $\mathsf{pk}$ to $\mathcal {A}$ and receives $\mathsf{msg}$ and sets $y=\mathbf {ECC}(\mathsf{msg})$.

• $\mathcal {C}$ draws $\mathbf {r}\leftarrow \chi _\sigma ^m$ and sets $\mathbf {u}^\mathsf{t}=\mathbf {r}^\mathsf{t}\mathbf {A}$ and $w_i=\mathbf {r}^\mathsf{t}\mathbf {v}_i+e_i'+(q/2)y_i$ for $i\in I_S$, where $e_i'\leftarrow \chi _{\sigma '}$. Then for each $i\in D_b$, $\mathcal {C}$ sets $z_i=b$ and $w_i=\mathbf {r}^\mathsf{t}\mathbf {v}_i+e_i'+(q/2)z_i$. Finally $\mathcal {C}$ sets $\mathsf{ct}=(\mathbf {u},w_1,\dots ,w_n)$ and $\mathsf{rand}=(I_S,\{z_i\}_{i\notin I_S},\mathbf {r},e_1',\dots ,e_n')$.

• $\mathcal {C}$ sends $(\mathsf{ct},\mathsf{sk},\mathsf{rand})$.

Claim

$H_3\approx _\mathsf{c} H_2$.

Proof Sketch

This follows from Claim 3.3, which states that the $(I_R,I_S,D_0,D_1)$ from $\mathsf{F}_\mathsf{real}$ is identical to the tuple drawn from $\mathsf{F}_\mathsf{ideal}$, combined with the fact that a PPT adversary cannot gain advantage by choosing $\mathsf{msg}$ after seeing $\mathsf{pk}$ rather than before or else it can be used to break LWE.      $\square$