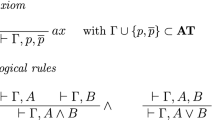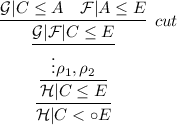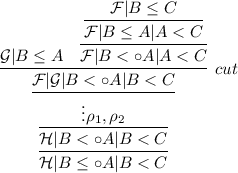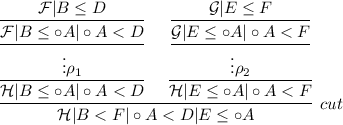Abstract
We consider an extension of propositional Gödel logic by an unary operator that enables the addition of a positive real to truth values. We provide a suitable calculus of relations and show completeness and cut elimination.
Partially supported by FWF grants P-26976-N25, I-1897-N25, I-2671-N35, and W1255-N23.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
c stands for ‘contraction’; w stands for ‘weakening’; com stands for ‘communication.’
References
Baaz, M., Ciabattoni, A., Fermüller, C.G.: Cut-elimination in a sequents-of-relations calculus for Gödel logic. In: Proceedings of The International Symposium on Multiple-Valued Logic, pp. 181–186 (2001)
Baaz, M., Fasching, O.: Monotone operators on Gödel logic. Arch. Math. Logic 53, 261–284 (2014)
Gabbay, D.M., Metcalfe, G., Olivetti, N.: Analytic sequent calculi for Abelian and Łukasiewicz logics. In: Egly, U., Fermüller, C. (eds.) TABLEAUX 2002. LNCS (LNAI), vol. 2381, pp. 191–205. Springer, Heidelberg (2002)
Gabbay, D., Metcalfe, G., Olivetti, N.: Proof Theory for Fuzzy Logics. Applied Logic, vol. 36. Springer, Netherlands (2008)
Takeuti, G.: Proof Theory. North-Holland, Amsterdam (1987)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
Proof of Lemma 14. The end-segment of the proof will be of the form

where \(C < \circ A\) and \(\circ A < D\) are inferred, respectively, at the hypersequents \(\mathcal {G}| C < \circ A\) and \(\mathcal {F}| \circ A < D\). We proceed according to which inferences were used above \(\mathcal {G}| C < \circ A\) and \(\mathcal {F}| \circ A < D\).
-
1.
If the inferences were respectively \(\circ _1\) or \(\circ _2\), so that the proof is

then replace it with
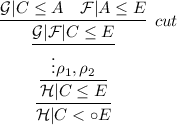
-
2.
If the inferences were both \(\circ _2\), so that the proof is

then replace it with

-
3.
If the inference on the left-hand side is \(\circ _1\) and the inference on the right-hand side is an internal weakening, the proof will be of the form

Replace it with
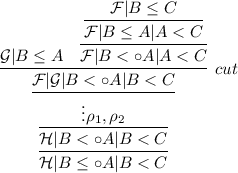
-
4.
If the inference on the left-hand side is \(\circ _2\) and the inference on the right-hand side is an internal weakening, the proof will be of the form

Replace it with

-
5.
If the inference on the right-hand side is \(\circ _2\) and the inference on the left-hand side is an internal weakening, the proof will be of the form

Replace it with

-
6.
The final case is that both inferences are internal weakenings:
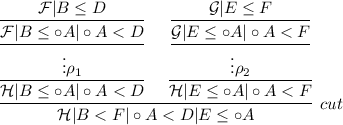
Replace it with

\(\quad \square \)
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Aguilera, J.P., Baaz, M. (2016). Cut Elimination for Gödel Logic with an Operator Adding a Constant. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds) Logic, Language, Information, and Computation. WoLLIC 2016. Lecture Notes in Computer Science(), vol 9803. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-52921-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-662-52921-8_3
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-52920-1
Online ISBN: 978-3-662-52921-8
eBook Packages: Computer ScienceComputer Science (R0)