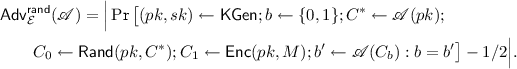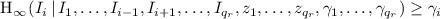Abstract
Inspired by the Dual EC DBRG incident, Dodis et al. (Eurocrypt 2015) initiated the formal study of backdoored PRGs, showing that backdoored PRGs are equivalent to public key encryption schemes, giving constructions for backdoored PRGs (BPRGs), and showing how BPRGs can be “immunised” by careful post-processing of their outputs. In this paper, we continue the foundational line of work initiated by Dodis et al., providing both positive and negative results.
We first revisit the backdoored PRG setting of Dodis et al., showing that PRGs can be more strongly backdoored than was previously envisaged. Specifically, we give efficient constructions of BPRGs for which, given a single generator output, Big Brother can recover the initial state and, therefore, all outputs of the BPRG. Moreover, our constructions are forward-secure in the traditional sense for a PRG, resolving an open question of Dodis et al. in the negative.
We then turn to the question of the effectiveness of backdoors in robust PRNGs with input (c.f. Dodis et al., ACM-CCS 2013): generators in which the state can be regularly refreshed using an entropy source, and in which, provided sufficient entropy has been made available since the last refresh, the outputs will appear pseudorandom. The presence of a refresh procedure might suggest that Big Brother could be defeated, since he would not be able to predict the values of the PRNG state backwards or forwards through the high-entropy refreshes. Unfortunately, we show that this intuition is not correct: we are also able to construct robust PRNGs with input that are backdoored in a backwards sense. Namely, given a single output, Big Brother is able to rewind through a number of refresh operations to earlier “phases”, and recover all the generator’s outputs in those earlier phases.
Finally, and ending on a positive note, we give an impossibility result: we provide a bound on the number of previous phases that Big Brother can compromise as a function of the state-size of the generator: smaller states provide more limited backdooring opportunities for Big Brother.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Background: In the wake of the Snowden revelations, the cryptographic research community has begun to realise that it faces a more powerful and insidious adversary than it had previously envisaged: Big Brother, an adversary willing to subvert cryptographic standards and implementations in order to gain an advantage against users of cryptography. The Dual EC DRBG debacle, and subsequent research showing the widespread use of this NIST-standardised pseudorandom generator (PRG) and its security consequences [11], has highlighted that inserting backdoors into randomness-generating components of systems is a profitable, if high-risk, strategy for Big Brother.
The threat posed by the Big Brother adversary brings new research challenges, both foundational and applied. The study of subversion of cryptographic systems — how to undetectably and securely subvert them, and how to defend against subversion — is a central one. Current research efforts to understand various forms of subversion include the study of Algorithm Substitution Attacks (ASAs) [2, 6, 13, 23, 28] and that of backdooring of cryptosystems [3, 8, 11, 15]. These lines of research have a long and rich history through topics such as kleptography [34] and subliminal channels [31]. In an ASA, the subversion is specific to a specific implementation of a particular algorithm or scheme, whereas in backdooring, the backdoor resides in the specification of the scheme or primitive itself and any implementation faithful to the specification will be equally vulnerable. There is a balancing act at play with these two types of attack: while ASAs are arguably easier to carry out, their impact is limited to a specific implementation, whereas the successful introduction of a backdoor into a cryptographic scheme, albeit ostensibly harder to mount and subsequently conceal, can have much wider impact.
The Importance of Randomness: Many cryptographic processes rely heavily on good sources of randomness, for example, key generation, selection of IVs for encryption schemes and random challenges in authentication protocols, and the selection of Diffie-Hellman exponents. Indeed randomness failures of various kinds have led to serious vulnerabilities in widely deployed cryptographic systems, with a growing literature on such failures [1, 7, 10, 19, 21, 22, 25, 27, 33]. Furthermore it is well established in the theory of cryptography that the security of most cryptographic tasks relies crucially on the quality of that randomness [16].
Since true random bits are hard to generate without specialised hardware, and such hardware has only recently started to become available on commodity computing platforms,Footnote 1 Pseudorandom Generators (PRGs) and Pseudorandom Number Generators with input (“PRNGs with input” for short) are almost universally used in implementations. These generate pseudorandom bits instead of truly random bits; PRNGs with input can also have their state regularly refreshed with fresh entropy, though from a possibly biased source of randomness. Typically, a host operating system will make PRNGs with input available to applications, with the entropy being gathered from a variety of events, e.g. keyboard or disk timings, or timing of interrupts and other system events; programming libraries typically also provide access to PRG functionality, though of widely varying quality.
Backdooring Randomness: Given the ubiquity of PRGs and PRNGs with input in cryptographic implementations, they constitute the ideal target for maximising the spread and impact of backdoors. This was probably the rationale behind the Dual EC DRBG [11] which is widely believed to have been backdoored by the NSA. Despite this generator’s low-speed, known output biases, and known capability to be backdoored (which was pointed out as early as 2007 by Shumow and Ferguson [30]), it managed to be covertly deployed in a range of widely used systems. Such systems continue to be discovered today, more than three years after the original Snowden revelations relating to Dual EC DRBG and project Bullrun.Footnote 2 The Dual EC DRBG provides a particularly useful backdoor to Big Brother: given a single output from the generator, its state can be recovered, and all future outputs can be recovered (with moderate computational effort). Protocols like SSL/TLS directly expose PRG outputs in protocol messages, making the Dual EC DRBG exploitable in practice [11].
Formal Analysis of Backdoored PRGs: The formal study of backdoored PRGs (BPRGs) was initiated by Dodis et. al. [15], building on earlier work of Vazirani and Vazirani [32]. Dodis et al. showed that BPRGs are equivalent to public-key encryption (PKE) with pseudorandom ciphertexts (IND$-CPA-security), provided constructions using PKE schemes and KEMs, and analysed folklore immunisation techniques. Understanding the nature of backdoored primitives together with their capabilities and limitations is an important first step towards finding solutions that will safeguard against backdooring attacks. For instance the equivalence of BPRGs with public key encryption shown in [15] suggests that a PRG based on purely symmetric techniques is less likely to contain a backdoor, since we currently do not know how to build public key encryption from one-way functions.
A basic question that was posed – and partly answered – in [15] is: to what extent can a PRG be backdoored while at the same time being provably secure? This question makes perfect sense in the context of subversion via backdooring, where the backdoor resides in the specification of the PRG itself, and where the PRG can be publicly assessed and its security evaluated. The Dual EC DRBG has notable biases which directly rule out any possibility of it being provably secure as a PRG. Nevertheless, in [15] it is noted that by using special encodings of curve points as in [9, 24, 35], these biases can be eliminated and the Dual EC DRBG can be turned into a provably forward-secure PRG under the DDH assumption.
Yet the backdoor in the Dual EC DRBG, while relatively powerful and certainly completely undermining security in certain applications like SSL/TLS, has its limitations. In particular, it does not allow Big Brother (who holds the backdoor key) to predict previous outputs from a given output but only future ones. The random-seek BPRG construction of [15] provides a stronger type of backdoor: given any single output, it allows Big Brother to recover any past or future output with probability roughly \(\frac{1}{4}\). But the random-seek BPRG construction of [15] attains this stronger backdooring at the expense of no longer being a forward-secure PRG (in the usual sense). Indeed, forward-security and the random-seek backdoor property would intuitively seem to be opposing goals, and it is then natural to ask whether this tradeoff is inherent, or whether strong forms of backdooring of forward-secure PRGs are possible. If the limitation was inherent, then a proof of forward-security for a PRG would serve to preclude backdoors with the backward-seek feature, so a forward-secure PRG would be automatically immunised, to some extent, against backdoors.
1.1 Our Contributions
In this work we advance understanding of backdoored generators in two distinct directions.
Stronger Backdooring of PRGs: We settle the above open question from [15] in the negative by providing two different constructions of random-seek BPRGs that are provably forward-secure. In fact we demonstrate something substantially stronger:
-
Firstly, both of our constructions allow Big Brother to succeed with probability 1 (rather than the 1/4 attained for the random-seek BPRG construction of [15]).
-
Secondly, the backdooring is much stronger, in that for both of our BPRG constructions, Big Brother is able to recover the initial state of the BPRG, given only a single output value. This then enables all states and output values to be reconstructed.
Our constructions require a number of cryptographic tools. Unsurprisingly, given the connection between BPRGs and PKE with pseudorandom ciphertexts that was shown in [15], they both make use of the latter primitive. To give a flavour of what lies ahead, we remark that our simplest construction, shown in Fig. 7, uses such a PKE scheme to encrypt its state \(s \), with the resulting ciphertext \(C \) forming the generator’s output; \(s \) is also evolved using a one-way function, to provide forward security. Clearly, Big Brother, with access to a single output and the decryption key, can recover the state \(s \). But we use a trapdoor one-way function so that Big Brother can then “unwind” \(s \) back to its starting value. For the security proof, we need to use a random oracle applied to \(s \) to generate the encryption randomness, making our construction reminiscent of the “Encrypt-with-hash” construction of [5], while for technical reasons, we require the trapdoor one-way function to be lossy [26]. Our second construction is in the standard model and combines, in novel ways, other primitives such as re-randomizable PKE schemes.
Backdooring PRNGs with Input: We then turn our attention to the study of backdoored PRNGs with input (BPRNGs). This is a very natural extension to the study of BPRGs conducted in [15] and continued here, particularly in view of the widespread deployment of PRNGs with input in real systems.
The formal study of PRNGs with input (but without backdooring) commenced with Barak and Halevi’s work in [4], later extended in [17, 18]. Various security notions have been proposed in the literature for PRNGs with input, namely resilience, forward security, backward security and robustness. Of these, robustness is the strongest notion. It captures the ability of a generator to both preserve security when its entropy inputs are influenced by an attacker and to recover security after its state is compromised, via refreshing (provided sufficient entropy becomes available to it). Robustness is generally accepted as the de facto security target for any new PRNG design, though several widely-deployed PRNGs fail to meet it (see, for example, [12, 17]).
Given that we are in the backdooring setting for subversion, in which the full specification of the cryptographic primitive targeted for backdooring is public, any construction can be vetted for security. It is therefore logical to require any BPRNG to be robust. (This is analogous to requiring a BPRG to be forward-secure, or at least, a PRG in the traditional sense.) As such, a BPRNG cannot just ignore its entropy inputs and revert to being a PRG. One might then hope that, with additional high entropy inputs being used to refresh the generator state, and with this entropy not being under the direct control of Big Brother (since, otherwise, no security at all is possible), backdooring a PRNG with input might be impossible. This would be a positive result in the quest to defeat backdooring. Unfortunately, we show that this is not the case.
As a warm-up, we show how to adapt the robust PRNG of [17] to make it backdoored. This requires only a simple trick (and some minor changes to the processing of entropy): replace the PRG component of the generator with a BPRG. Given a single output from the generator, this then allows Big Brother to compute all outputs from the last refresh operation to the next refresh operation. Yet the generator is still robust.
Much more challenging is to develop a robust PRNG with input in which Big Brother can use his backdoor to “pass through” refresh operations when computing generator outputs. We provide a construction which does just that, see Fig. 11. Our construction is based on the idea of interleaving outputs of a (non-backdoored) PRNG with encryptions of snapshots of that PRNG’s state, using an  secure encryption scheme to ensure pseudorandomness of the outputs. By taking a snapshot of the state whenever it is refreshed and storing a list of the previous k snapshots in the state (for a parameter k), the construction enables Big Brother to recover, with some probability, old output values that were computed as many as k refreshes previously. The actual construction is considerably more complex than this sketch hints, since achieving robustness, in the sense of [17], is challenging when the state has this additional structure. We also sketch variants of this construction that trade state and output size for strength of backdooring.
secure encryption scheme to ensure pseudorandomness of the outputs. By taking a snapshot of the state whenever it is refreshed and storing a list of the previous k snapshots in the state (for a parameter k), the construction enables Big Brother to recover, with some probability, old output values that were computed as many as k refreshes previously. The actual construction is considerably more complex than this sketch hints, since achieving robustness, in the sense of [17], is challenging when the state has this additional structure. We also sketch variants of this construction that trade state and output size for strength of backdooring.
An Impossibility Result for BPRNGs: We close the paper on a more positive note, providing an impossibility result showing that backdooring in a strong sense cannot be achieved (whilst preserving robustness) without significantly enlarging the state of the generator. More precisely, we show that it is not possible for Big Brother to perform a state recovery attack in which he recovers more than some number k of properly refreshed previous states from an output of the generator, when k is large relative to the state-size of the BPRNG. A precise formalisation of our result is contained in Theorem 5.
Note that the backdooring attack here requires more of Big Brother than might be needed in practice, since he may be considered successful if he can recover just one previous state, or a fraction of the previous BPRNG outputs. Our construction shows that backdooring of this kind is certainly possible. Nor does our result say anything about Big Brother’s capabilities (or lack thereof) when it comes to recovering future states/outputs (after a generator has undergone further high-entropy refresh operations). It is an important open problem to strengthen our impossibility results – and to improve our constructions – to explore the limits of backdooring for PRNGs with input.
2 Preliminaries
2.1 Notation
The set of binary strings of length n is denoted \(\{0,1\}^n\) and \(\varepsilon \) denotes the empty string. For any two binary strings x and y we write |x| to denote the size of x and \(x\Vert y\) to denote their concatenation. For any set U we denote by \(u \twoheadleftarrow U\) the process of sampling an element uniformly at random from U and assigning it to u. All logs are to base 2.
2.2 Entropy
We recall a number of standard definitions on entropy, statistical distance, and \((k, \epsilon )\)-extractors in the full version [14].
Definition 1
An \((k, \epsilon )\)-extractor \(\mathsf {Ext}: \{0,1\}^* \times \{0,1\}^v \rightarrow \{0,1\}^w\) is said to be online-computable on inputs of length p if there exists a pair of efficient algorithms \({\mathsf {iterate}}: \{0,1\}^p \times \{0,1\}^p \times \{0,1\}^v \rightarrow \{0,1\}^p \), and \({\mathsf {finalize}}: \{0,1\}^p \times \{0,1\}^v \rightarrow \{0,1\}^w\) such that for all inputs \(\bar{I} = (I_1, \dots , I_d)\) where each \(I_j \in \{0,1\}^p\), and \(d\ge 2\), then after setting \(y _1 = I_1\), and \(y _j = {\mathsf {iterate}}(y _{j-1}, I_j; \text {A})\) \(j=2, \dots , d\), it holds that
2.3 Cryptographic Primitives
In the full version [14], we recall a number of standard definitions for PKE schemes. Throughout this work we require that PKE schemes be length-regular. For the constructions that follow, we shall require an  -secure PKE scheme; that is to say a PKE scheme having pseudorandom ciphertexts. We define such schemes formally below. Concrete and efficient examples of such schemes can be obtained by applying carefully constructed encoding schemes to the group elements of ciphertexts in the ElGamal encryption scheme (in which ciphertexts are of the form \((g^{R},M \cdot g^{R x})\) where g generates a group of prime order p in which DDH is hard; \((g^x,x) \leftarrow \mathsf {KGen}\) with \(x \twoheadleftarrow \mathbb {Z}_p\); \(R \twoheadleftarrow \mathbb {Z}_p\); and \(M \) is a message, encoded here as a group element); see for example [9, 24, 35].
-secure PKE scheme; that is to say a PKE scheme having pseudorandom ciphertexts. We define such schemes formally below. Concrete and efficient examples of such schemes can be obtained by applying carefully constructed encoding schemes to the group elements of ciphertexts in the ElGamal encryption scheme (in which ciphertexts are of the form \((g^{R},M \cdot g^{R x})\) where g generates a group of prime order p in which DDH is hard; \((g^x,x) \leftarrow \mathsf {KGen}\) with \(x \twoheadleftarrow \mathbb {Z}_p\); \(R \twoheadleftarrow \mathbb {Z}_p\); and \(M \) is a message, encoded here as a group element); see for example [9, 24, 35].
Definition 2
A PKE scheme \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) is said to be \((t, q, \delta )\)- -secure if for all adversaries \(\mathscr {A}\) running in time t and making at most q oracle queries, it holds that
-secure if for all adversaries \(\mathscr {A}\) running in time t and making at most q oracle queries, it holds that  , where:
, where:

and \(\$(\cdot )\) is such that on input a message \(M \) it returns a random string of size \(|\mathsf {Enc}(pk,M)|\).
It is straightforward to show that if \(\mathcal {E} \) is \((t, q, \delta )\)- -secure, then it is also \((t, q, 2\delta )\)-
-secure, then it is also \((t, q, 2\delta )\)- -secure in the usual sense.
-secure in the usual sense.
We shall also utilise PKEs which are statistically re-randomizable; again the ElGamal scheme and its group-element-encoded variants have the required property.
Definition 3
[20] A \((t, q, \delta , \nu )\)-statistically re-randomizable encryption scheme is a tuple of algorithms \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Rand}, \mathsf {Dec})\) where \((\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) is a standard PKE scheme and \(\mathsf {Rand}\) is an efficient randomised algorithm such that for all \((pk,sk) \leftarrow \mathsf {KGen}\) and for all \(M, R _0^\prime \),

That is, the distributions of an honestly generated ciphertext and a ciphertext obtained by applying \(\mathsf {Rand}\) to one generated with arbitrary randomness are statistically close. We write \(\mathsf {Rand}(C _0; R _1, \dots , R _q)\) to denote the value of \(C _q\) where \(C _j = \mathsf {Rand}(C _{j-1}; R _j)\) for \(j = 1, \dots , q\).
We now define encryption schemes which have the additional property of being reverse re-randomizable. It is easy to see that ElGamal encryption and its encoded variants has the required property.
Definition 4
A \((t, q, \delta , \nu )\)-statistically reverse re-randomizable encryption scheme \(\mathcal {E}\) is a tuple of algorithms \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Rand}, \mathsf {Rand^{-1}}, \mathsf {Dec}) \) such that:
-
\((\mathsf {KGen}, \mathsf {Enc}, \mathsf {Rand}, \mathsf {Dec})\) is a \((t, q, \delta , \nu )\) statistically re-randomizable encryption scheme.
-
\(\mathsf {Rand^{-1}}\) is an efficient algorithm such that for all \((pk,sk) \leftarrow \mathsf {KGen}\) and for all \(M \),\(R _0\),\(R _1\), it holds that, if \(C = \mathsf {Enc}(pk, M; R _0)\), then:
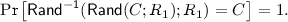
Suppose \(C _q = \mathsf {Rand}(C _0; R _1, \dots , R _q)\), so that \(C _j = \mathsf {Rand}(C _{j-1}; R _j)\) for \(j = 1, \dots , q\). Then, from the above, we know that \(C _{j-1} = \mathsf {Rand^{-1}}(C _{j}; R _j)\) for \(1 \le j \le q\); to denote \(C _0\), we write \(\mathsf {Rand^{-1}}(C _q; R _1, \dots , R _q)\).
We recall the definitions of trapdoor one-way permutations, and lossy trapdoor permutations, in the full version [14].
2.4 Pseudorandom Generators
A pseudorandom generator (\(\mathrm {PRG}\)) takes a small amount of true statistical randomness as an input seed, and outputs arbitrary (polynomial) length bit-strings which are pseudorandom. Following [15], we will equip \(\mathrm {PRG}\)s with a parameter generation algorithm, \({\mathsf {setup}} \). This allows backdooring to be introduced into the formalism.
Definition 5
A \(\mathrm {PRG}\) is a triple of algorithms \({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} )\), with associated parameters \((n,l)\in \mathbb {N}^2\), defined as follows:
-
\({\mathsf {setup}} : \{0,1\}^* \rightarrow \{0,1\}^* \times \{0,1\}^*\) takes random coins as input and outputs a pair of parameters \((pp, bk)\), where \(pp\) denotes the public parameter for the generator, and \(bk\) is the secret backdoor parameter. In a non-backdoored \(\mathrm {PRG}\), we set \(bk = \perp \).
-
\({\mathsf {init}} : \{0,1\}^* \times \{0,1\}^* \rightarrow \{0,1\}^n\) takes \(pp\) and random coins as input, and returns an initial state for the \(\mathrm {PRG}\), \(s _0\in \{0,1\}^n.\)
-
\({\mathsf {next}} : \{0,1\}^* \times \{0,1\}^n \rightarrow \{0,1\}^l \times \{0,1\}^n \) takes \(pp\) and a state \(s \in \{0,1\}^n\) as input, and outputs an output/state pair \((r, s ^\prime )\leftarrow {\mathsf {next}} (pp, s)\) where \(r \in \{0,1\}^l\) is the \(\mathrm {PRG}\)’s output, and \(s ^\prime \in \{0,1\}^n\) is the updated state.
Definition 6
Let \({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} )\) be a \(\mathrm {PRG}\). Given an initial state \(s _0\), we set \((r _i,s _i) \leftarrow {\mathsf {next}} (pp, s _{i-1})\) for \(i=1,\ldots ,q\). We write \(\textsf {out} ^q({\mathsf {next}} (pp, s _0))\) for the sequence of outputs \(r _1,\ldots ,r _q\) and \(\textsf {state} ^q({\mathsf {next}} (pp, s _0))\) for the sequence of states \(s _1,\ldots ,s _q\) produced by this process.
Definition 7
(PRG Security). Let \({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} )\) be a \(\mathrm {PRG}\). Consider the game  of Fig. 1 in which the adversary receives either q outputs from the \(\mathrm {PRG}\) or q random strings of the appropriate size. We define the \(\mathrm {PRG}\) distinguishing advantage of \(\mathscr {A}\) against \({\mathsf {PRG}}\) to be
of Fig. 1 in which the adversary receives either q outputs from the \(\mathrm {PRG}\) or q random strings of the appropriate size. We define the \(\mathrm {PRG}\) distinguishing advantage of \(\mathscr {A}\) against \({\mathsf {PRG}}\) to be

Definition 8
A \(\mathrm {PRG}\) \({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} )\) is said to be \((t, q, \delta )\)-secure if for all adversaries \(\mathscr {A}\) running in time at most t it holds that  .
.
Definition 9
(PRG Forward Security). Let \({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} )\) be a \(\mathrm {PRG}\). Consider the game  of Fig. 1 in which the adversary receives either q outputs from the \(\mathrm {PRG}\) and the final state, or q random strings of the appropriate size and the final state. We define the \(\mathrm {PRG}\) forward-security advantage of \(\mathscr {A}\) against \({\mathsf {PRG}}\) to be
of Fig. 1 in which the adversary receives either q outputs from the \(\mathrm {PRG}\) and the final state, or q random strings of the appropriate size and the final state. We define the \(\mathrm {PRG}\) forward-security advantage of \(\mathscr {A}\) against \({\mathsf {PRG}}\) to be

Definition 10
A \(\mathrm {PRG}\) \({\mathsf {PRG}} \) is said to be \((t, q, \delta )\)-\(\mathrm {FWD}\)-secure if for all adversaries \(\mathscr {A}\) running in time at most t it holds that  .
.
2.5 Backdoored Pseudorandom Generators
The first formal treatment of backdoored \(\mathrm {PRG}\)s was that of Dodis et al. [15]. Intuitively, a backdoored cryptosystem is a scheme coupled with some secret backdoor information. In the view of an adversary who does not know the backdoor information, the scheme fulfils its usual security definition. However an adversary in possession of the backdoor information will gain some advantage in breaking the security of the cryptosystem. The backdoor attacker is modelled as an algorithm which we call \(\mathscr {B} \) (for ‘Big Brother’), to distinguish it from an attacker \(\mathscr {A} \) whose goal is to break the usual security of the scheme without access to the backdoor. Whilst the backdoor attacker \(\mathscr {B} \) will be external in the sense that it will only be able to observe public outputs and parameters, the attack is also internalised as the backdoor algorithm is designed alongside, and incorporated into, the scheme.
We define backdoored \(\mathrm {PRG}\)s (BPRGs) in conjunction with different games  which capture specific backdooring goals, each game having a corresponding advantage term. The three games considered in [15] are defined in Fig. 2.
which capture specific backdooring goals, each game having a corresponding advantage term. The three games considered in [15] are defined in Fig. 2.
Definition 11
A tuple of algorithms \(\overline{{\mathsf {PRG}}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) is defined to be a \((t, q, \delta , ({\textsf {type}} , \epsilon ))\)-secure \(\mathrm {BPRG}\) if:
-
\({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} )\) is a \((t, q, \delta )\)-secure PRG;
-
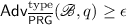 .
.
Definition 12
Let \(\overline{{\mathsf {PRG}}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) be a \(\mathrm {BPRG}\). We define
-
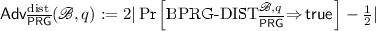 ,
, -
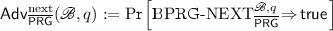 ,
, -
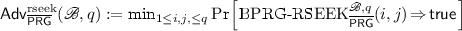 .
.
In Fig. 2, game  challenges Big Brother to use the backdoor to break the security of the \(\mathrm {PRG}\) in the most basic sense of distinguishing real from random outputs. In game
challenges Big Brother to use the backdoor to break the security of the \(\mathrm {PRG}\) in the most basic sense of distinguishing real from random outputs. In game  , \(\mathscr {B} \) aims to recover the current state of the \(\mathrm {PRG}\) given q consecutive outputs from the generator. This is a far more powerful compromise since it then allows \(\mathscr {B} \) to predict all of the generator’s future outputs. In the third game,
, \(\mathscr {B} \) aims to recover the current state of the \(\mathrm {PRG}\) given q consecutive outputs from the generator. This is a far more powerful compromise since it then allows \(\mathscr {B} \) to predict all of the generator’s future outputs. In the third game,  , \(\mathscr {B} \) is given only the \(i^{th}\) output (rather than q outputs) and index j, and tries to recover the \(j^\text {th}\) output (but not any state).
, \(\mathscr {B} \) is given only the \(i^{th}\) output (rather than q outputs) and index j, and tries to recover the \(j^\text {th}\) output (but not any state).
It is noted in [15] that an adversary \(\mathscr {B} \) winning in game  represents a stronger form of backdooring than an adversary \(\mathscr {B} \) winning in game
represents a stronger form of backdooring than an adversary \(\mathscr {B} \) winning in game  for the same parameters, whilst an adversary \(\mathscr {B} \) winning in game
for the same parameters, whilst an adversary \(\mathscr {B} \) winning in game  may be more or less powerful than one for game
may be more or less powerful than one for game  depending on the circumstances. The paper [15] presents constructions of BPRGs that are backdoored in the
depending on the circumstances. The paper [15] presents constructions of BPRGs that are backdoored in the  and
and  senses, but does also note that their construction for a scheme of the latter type is not forward-secure.
senses, but does also note that their construction for a scheme of the latter type is not forward-secure.
Both for their intrinsic interest, and because they will be needed in our later constructions of backdoored PRNGs with input, we are interested in BPRGs that are forward secure against normal adversaries. For a generic type of game  , these are formally defined as follows.
, these are formally defined as follows.
Definition 13
A tuple of algorithms \(\overline{{\mathsf {PRG}}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) is said to be a \((t, q, \delta , ({\textsf {type}}, \epsilon ))\)-\(\mathrm {FWD}\)-secure \(\mathrm {BPRG}\) if:
-
\({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} )\) is a \((t, q, \delta )\)-\(\mathrm {FWD}\)-secure PRG;
-
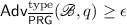 .
.
2.6 Pseudorandom Number Generators with Input
Definition 14
(PRNG with Input). A \(\mathrm {PRNG}\) with input is a tuple of algorithms \({\mathsf {PRNG}} =({\mathsf {setup}},{\mathsf {init}},{\mathsf {refresh}},{\mathsf {next}})\) with associated parameters \((n,l,p)\in \mathbb {N}^3\), where:
-
\({\mathsf {setup}}:\{0,1\}^*\rightarrow \{0,1\}^*\) takes as input some random coins and returns a public parameter \(pp \).
-
\({\mathsf {init}}:\{0,1\}^*\times \{0,1\}^*\rightarrow \{0,1\}^n\) takes the public parameter \(pp \) and some random coins to return an initial state \(s _0\).
-
\({\mathsf {refresh}}:\{0,1\}^*\times \{0,1\}^n\times \{0,1\}^p\rightarrow \{0,1\}^n\) takes as input the public parameter \(pp \), the current state S, and a sample I from the entropy source, and returns a new state \(s '\).
-
\({\mathsf {next}}:\{0,1\}^*\times \{0,1\}^n\rightarrow \{0,1\}^n\times \{0,1\}^l\) takes as input the public parameter \(pp \) and the current state \(s \), and returns a new state \(s '\) together with an output string \(r\).
Definition 15
(Distribution Sampler). A distribution sampler \(\mathscr {D}:\{0,1\}^*\rightarrow \{0,1\}^*\times \{0,1\}^p\times \mathbb {R}^{\ge 0}\times \{0,1\}^*\) is a probabilistic and possibly stateful algorithm which takes its current state \(\sigma \) as input and returns an updated state \(\sigma '\), a sample I, an entropy estimate \(\gamma \), and some leakage information z about I. The state \(\sigma \) is initialised to the empty string.
A distribution sampler \(\mathscr {D}\) is said to be valid up to \(q_r\) samples, if for all \(j\in \{1,\dots ,q_r \}\) it holds (with probability 1) that:

where \((\sigma _i,I_i,\gamma _i,z_i)=\mathscr {D} (\sigma _{i-1})\) for \(i\in \{1,\dots ,q_r \}\) and \(\sigma _0=\varepsilon \).
2.7 Security for Pseudorandom Number Generators with Input
We now turn to discussing security definitions for PRNGs with input. We follow [17], with some minor differences noted below.
Definition 16
(Security of \(\mathrm {PRNG}\) with Input). With references to the security game shown in Fig. 3, a \(\mathrm {PRNG}\) with input \({\mathsf {PRNG}} =({\mathsf {setup}},{\mathsf {init}},{\mathsf {refresh}},{\mathsf {next}})\) is said to be  -secure, for any distribution sampler \(\mathscr {D}\) valid up to \(q_r\) samples, and any adversary \(\mathscr {A}\) running in time at most t, making at most \(q_r\) queries to \({\textsc {Ref}}\), \(q_n\) queries to \({\textsc {Ror}}\) and a total of \(q_c\) queries to \({\textsc {Get}}\) and \({\textsc {Set}}\), the corresponding advantage in game \(\mathrm {ROB} ^{\mathscr {D},\mathscr {A}}_{{\mathsf {PRNG}},\gamma ^*}\)is bounded by \(\epsilon \), where
-secure, for any distribution sampler \(\mathscr {D}\) valid up to \(q_r\) samples, and any adversary \(\mathscr {A}\) running in time at most t, making at most \(q_r\) queries to \({\textsc {Ref}}\), \(q_n\) queries to \({\textsc {Ror}}\) and a total of \(q_c\) queries to \({\textsc {Get}}\) and \({\textsc {Set}}\), the corresponding advantage in game \(\mathrm {ROB} ^{\mathscr {D},\mathscr {A}}_{{\mathsf {PRNG}},\gamma ^*}\)is bounded by \(\epsilon \), where

Our definition here deviates from that in [17] in the following ways.
-
We generalise the syntax so as to allow the state to be initialised according to some arbitrary distribution rather than requiring it to be uniformly random. In particular we allow this distribution to depend on \(pp\). This facilitates our backdooring definitions to follow.
-
We have removed the \({\textsc {Next}} \) oracle from the model, without any loss of generality (as was shown in [12]).
One of the key insights of [17] is to decompose the somewhat complex notion of robustness into the two simpler notions of \(\mathrm {PRE}\)and \(\mathrm {REC}\) security. We recall these definitions below, generalised here to include the \({\mathsf {init}}\) algorithm.
Definition 17
(Preserving and Recovering Security). Consider the security games described in Fig. 4. The \(\mathrm {PRE}\)security advantage of an adversary \(\mathscr {A}\) against a \(\mathrm {PRNG}\) with input \({\mathsf {PRNG}}\) is defined to be

The \(\mathrm {REC}\) security advantage with respect to parameters \(q_r\), \(\gamma ^*\) of an adversary/sampler pair (\(\mathscr {A}\), \(\mathscr {D}\)) against a \(\mathrm {PRNG}\) with input \({\mathsf {PRNG}}\) is defined to be

In the \(\mathrm {REC}\) security game, it is required that \(\sum \nolimits _{j=k+1}^{k+d}\varvec{\gamma } [j]\ge \gamma ^* \) for the value d output by \(\mathscr {A}\).
Definition 18
(Preserving Security). A \(\mathrm {PRNG}\) with input \({\mathsf {PRNG}}\) is said to have \((t, \epsilon _{pre})\)-\(\mathrm {PRE}\)security if for all attackers \(\mathscr {A}\) running in time t, it holds that  .
.
Definition 19
(Recovering Security). A \(\mathrm {PRNG}\) with input \({\mathsf {PRNG}}\) is said to have \((t, q_r, \gamma ^*, \epsilon _{rec})\)-\(\mathrm {REC}\) security if for any attacker \(\mathscr {A}\) and sampler \(\mathscr {D}\) valid up to \(q_r\) samples and running in time t, it holds that  .
.
Informally, preserving security concerns a generator’s ability to maintain security (in the sense of having pseudorandom state and output) when the adversary completely controls the entropy source used to refresh the generator but does not compromise its state. Meanwhile, recovering security captures the idea that a generator whose state is set by the adversary should eventually get to a secure state, and start producing pseudorandom outputs, once sufficient entropy has been made available to it. The proof of Theorem 1 can be found in the full version [14].
Theorem 1
Let \({\mathsf {PRNG}}\) be a \(\mathrm {PRNG}\) with input. If \({\mathsf {PRNG}}\) has both \((t, \epsilon _{pre})\)-\(\mathrm {PRE}\) security, and \((t, q_r, \gamma ^*, \epsilon _{rec})\)-\(\mathrm {REC}\) security, then \({\mathsf {PRNG}}\) is \(((t^\prime , q_r, q_n, q_c), \gamma ^*, \epsilon )\)-\(\mathrm {ROB}\) secure where \(t \approx t^\prime \) and \(\epsilon = q_n (\epsilon _{pre} + \epsilon _{rec})\).
To simplify notation, we will make use of an algorithm, \(\textsf {evolve}\), to generate output values and update the internal state of a PRNG. It takes as input a PRNG with input \({\mathsf {PRNG}} = ({\mathsf {setup}}, {\mathsf {init}}, {\mathsf {next}}, {\mathsf {refresh}})\), public parameter \(pp\), an initial state \(s \), a refresh pattern \({{\varvec{rp}}}= (a_1,b_1,\ldots ,a_{\rho },b_{\rho })\), and a distribution sampler \(\mathscr {D}\). The refresh pattern rp denotes a sequence of calls to \({\mathsf {next}}\) and \({\mathsf {refresh}}\); for each i, \(a_i\) denotes the number of consecutive calls to \({\mathsf {next}}\) and \(b_i\) denotes the subsequent number of consecutive calls to \({\mathsf {refresh}}\). More specifically, \(\textsf {evolve}\) proceeds as shown in Fig. 5.
The output of \(\textsf {evolve}\) is a sequence, \((r _1,s _1,\ldots ,r _{q_n },s _{q_n })\), of PRNG output and state pairs, where \(q_n = \sum _{i=1}^{\rho } a_i\). Based on \(\textsf {evolve}\), we define an additional algorithm, \({\textsf {out}}\), which takes the same input, runs \(\textsf {evolve}\), and returns only the output values \((r _1,\ldots ,r _{q_n })\).
3 Stronger Models and New Constructions for Backdoored Pseudorandom Generators
In this section, we first present two new, strong backdooring security models for PRGs. The stronger of the two implies all the backdooring notions in [15]. We then give two new constructions of BPRGs which achieve our two backdooring notions. In contrast to the strongest constructions in [15], all of our constructions are forward-secure.
3.1 Backdoored \(\mathrm {PRG}\) Security Models
In the first of our two new models, the BPRG is run with initial state \(s _0\) to produce q outputs \(r _1,\ldots ,r _q\). The Big Brother adversary \(\mathscr {B} \) is then given a particular output \(r _i\), and challenged to recover the initial state \(s _0\) of the BPRG. In the second model, the BPRG is again run with initial state \(s _0\) to produce q outputs, one of which is given to \(\mathscr {B} \). However \(\mathscr {B} \) is now asked to reproduce the remaining \(q-1\) unseen output values. We formalise these two models as games  and
and  in Fig. 6.
in Fig. 6.
Definition 20
Let \(\overline{{\mathsf {PRG}}} =({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) be a \(\mathrm {BPRG}\). We define
-
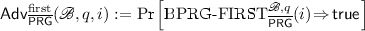 , and
, and -
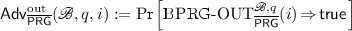
Discussion. We observe that our first backdooring notion, as formalised in  and
and  , is strictly stronger than the three notions for \(\mathrm {BPRG}\)s defined in [15] and discussed in Sect. 2.5: it is straightforward to see that any \((t, q, \delta , ({{\textsf {first}}}, \epsilon ))\)-secure \(\mathrm {BPRG}\) is also a \((t, q, \delta , ({\textsf {type}} , \epsilon ))\)-secure \(\mathrm {BPRG}\) for \({\textsf {type}} \in \{{\textsf {dist}}, {\textsf {state}}, {\textsf {rseek}} \}\).
, is strictly stronger than the three notions for \(\mathrm {BPRG}\)s defined in [15] and discussed in Sect. 2.5: it is straightforward to see that any \((t, q, \delta , ({{\textsf {first}}}, \epsilon ))\)-secure \(\mathrm {BPRG}\) is also a \((t, q, \delta , ({\textsf {type}} , \epsilon ))\)-secure \(\mathrm {BPRG}\) for \({\textsf {type}} \in \{{\textsf {dist}}, {\textsf {state}}, {\textsf {rseek}} \}\).
Moreover, simple comparison of definitions shows that any \((t, q, \delta , ({{\textsf {out}}}, \epsilon ))\)-secure \(\mathrm {BPRG}\) is also a \((t, q, \delta , ({\textsf {type}} , \epsilon ))\)-secure \(\mathrm {BPRG}\) for \({\textsf {type}} \in \{{\textsf {dist}}, {\textsf {rseek}} \}\). However, a \(\mathrm {BPRG}\) backdoored in the \({{\textsf {out}}} \) sense need not be backdoored in the \({\textsf {state}} \) sense, since the latter concerns state prediction rather than output prediction. (And indeed it is easy to construct separating examples for the \({{\textsf {out}}} \) and \({\textsf {state}} \) backdooring notions.)
Since the initial state of a \(\mathrm {PRG}\) determines all of its output, it is also clear that any \((t, q, \delta , ({{\textsf {first}}}, \epsilon ))\)-secure BRPG is also a \((t, q, \delta , ({{\textsf {out}}}, \epsilon ))\)-secure \(\mathrm {BPRG}\). However, the converse need not hold, and \({{\textsf {first}}} \) backdooring is strictly stronger than \({{\textsf {out}}} \) backdooring. To see this, consider \(\overline{{\mathsf {PRG}}} \), a \((t, q, \delta , ({{\textsf {out}}}, \epsilon ))\)-secure \(\mathrm {BPRG}\), and define a modified BRPG \(\overline{{\mathsf {PRG}}} ^\prime \) in which the initial state \(s _0\) is augmented to \(s _0||d\) for \(d \twoheadleftarrow \{0,1\}^n\), but where d is not used in any computations and all other algorithms of \(\overline{{\mathsf {PRG}}} \) are left unchanged. In particular, the output produced by \(\overline{{\mathsf {PRG}}} ^\prime \) is identical to that of \(\overline{{\mathsf {PRG}}} \). Then it is easy to see that \(\overline{{\mathsf {PRG}}} ^\prime \) is a \((t, q, \delta , ({{\textsf {out}}}, \epsilon ))\)-secure \(\mathrm {BPRG}\), but that  , since \(\mathscr {B} \) can do no better than guessing the n extra bits of state d.
, since \(\mathscr {B} \) can do no better than guessing the n extra bits of state d.
In most attack scenarios, and taking Big Brother’s perspective, the ability of \(\mathscr {B} \) to compute all unseen output (as in \({{\textsf {out}}} \)) is as useful in practice as being able to compute the initial state (as in \({{\textsf {first}}} \)), since it is the output values of the BPRG that will be consumed in applications. This makes the \({{\textsf {out}}} \) notion a natural and powerful target for constructions of \(\mathrm {BPRG}\)s. That said, in the sequel we will obtain constructions for the even stronger \({{\textsf {first}}} \) setting.
A \((t, q, \delta , ({\textsf {rseek}} , \epsilon ))\)-secure \(\mathrm {BPRG}\) is also a \((t, q, \delta , ({{\textsf {out}}}, \epsilon ^{q-1}))\)-secure \(\mathrm {BPRG}\), implying an exponential loss in going from \({\textsf {rseek}} \) backdooring to \({{\textsf {out}}} \) backdooring. This means that achieving either \({{\textsf {first}}} \) or \({{\textsf {out}}} \) backdooring with a high value of \(\epsilon \) is significantly more powerful than achieving \({\textsf {rseek}} \) backdooring with the same \(\epsilon \).
3.2 Forward-Secure \(\mathrm {BPRG}\)s in the Random Oracle Model
We present our first construction for a forward-secure \(\mathrm {BPRG}\) that is backdoored in the \({{\textsf {first}}} \) sense in Fig. 7. This construction uses as ingredients an LTDP family and an  -secure PKE scheme. Its security analysis is in the Random Oracle Model (ROM). It achieves our strongest \({{\textsf {first}}} \) notion with \(\epsilon =1\).
-secure PKE scheme. Its security analysis is in the Random Oracle Model (ROM). It achieves our strongest \({{\textsf {first}}} \) notion with \(\epsilon =1\).
The scheme is reminiscent of the “Encrypt-with-Hash” paradigm for constructing deterministic encryption schemes from [5]. At each stage, the generator encrypts its own state \(s \), with randomness derived from hashing \(s \), to produce the next output. The  -security of the PKE scheme ensures these outputs are pseudorandom. The state \(s \) is also transformed by applying a one-way function \(\mathsf {F} \) at each stage. This is necessary to provide forward security against non-\(\mathscr {B} \) adversaries. The function is trapdoored, enabling \(\mathscr {B} \) to decrypt an output to recover a state, then reverse the state update repeatedly to recover the initial state, thereby realising \({{\textsf {first}}} \) backdooring. For technical reasons that will become apparent in the proof, we require the one-way function \(\mathsf {F} \) to be a lossy permutation. The proof of the following theorem can be found in the full version [14].
-security of the PKE scheme ensures these outputs are pseudorandom. The state \(s \) is also transformed by applying a one-way function \(\mathsf {F} \) at each stage. This is necessary to provide forward security against non-\(\mathscr {B} \) adversaries. The function is trapdoored, enabling \(\mathscr {B} \) to decrypt an output to recover a state, then reverse the state update repeatedly to recover the initial state, thereby realising \({{\textsf {first}}} \) backdooring. For technical reasons that will become apparent in the proof, we require the one-way function \(\mathsf {F} \) to be a lossy permutation. The proof of the following theorem can be found in the full version [14].
Theorem 2
Let \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) be a \((t, q, \delta )\)- secure PKE scheme. Let \({\mathsf {LTDP}} = (\mathsf {G} _0, \mathsf {G} _1, \mathsf {S}, \mathsf {F}, \mathsf {F} ^{-1})\) be a family of \((n, k, t, \epsilon )\)-lossy trapdoor permutations. Then \(\overline{{\mathsf {PRG}}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) with algorithms as shown in Fig. 7 is a \((t^\prime , q, (2\delta + 3\epsilon + (q+1)2^{-(k-1)}), ({{\textsf {first}}} , 1))\)-\(\mathrm {FWD}\)secure \(\mathrm {BPRG}\) in the ROM, where \(t^\prime \approx t\).
secure PKE scheme. Let \({\mathsf {LTDP}} = (\mathsf {G} _0, \mathsf {G} _1, \mathsf {S}, \mathsf {F}, \mathsf {F} ^{-1})\) be a family of \((n, k, t, \epsilon )\)-lossy trapdoor permutations. Then \(\overline{{\mathsf {PRG}}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) with algorithms as shown in Fig. 7 is a \((t^\prime , q, (2\delta + 3\epsilon + (q+1)2^{-(k-1)}), ({{\textsf {first}}} , 1))\)-\(\mathrm {FWD}\)secure \(\mathrm {BPRG}\) in the ROM, where \(t^\prime \approx t\).
Construction of a forward-secure \(\mathrm {BPRG}\) \(({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) from an LTDP family \({\mathsf {LTDP}} = (\mathsf {G} _0, \mathsf {G} _1, \mathsf {S}, \mathsf {F}, \mathsf {F} ^{-1})\) and an  -secure PKE scheme \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\).
-secure PKE scheme \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\).
3.3 Standard Model, Forward-Secure BPRGs from Reverse Re-randomizable Encryption
Our second construction dispenses with the ROM and the use of lossy trapdoor permutations, at the expense of requiring as a component an  -secure reverse re-randomizable PKE scheme (see Definition 4). It is instantiable in the standard model using a variant of the ElGamal encryption scheme. The scheme is again backdoored in the \({{\textsf {first}}}\) sense with \(\epsilon =1\).
-secure reverse re-randomizable PKE scheme (see Definition 4). It is instantiable in the standard model using a variant of the ElGamal encryption scheme. The scheme is again backdoored in the \({{\textsf {first}}}\) sense with \(\epsilon =1\).
The scheme, shown in Fig. 8, uses algorithm \({\mathsf {next}} ^\prime \) from a normal (forward-secure) PRG \({\mathsf {PRG}} ^\prime \) to generate the next state \(s ^\prime \) and a pseudorandom value \(t \) using the current state \(s \) as a seed. The value \(t \) is then used to re-randomise a ciphertext \(C \) that encrypts an initial state value \(s _0\), and the ‘old’ value \(C \) is used as the generator’s output \(r \). The re-randomisation at each step ensures that the outputs collectively appear pseudorandom to a regular PRG adversary; the fact that \({\mathsf {PRG}} ^\prime \) is forward-secure ensures that the constructed \(\mathrm {BPRG}\) is too.
Meanwhile, the use of PKE allows \(\mathscr {B} \) (who knows the decryption key) to recover \(s _0\) from any of the generator’s outputs, run the component generator \({\mathsf {PRG}} ^\prime \) from its starting state \(s _0\), and recover all the values \(t \) used for re-randomisation at each step; finally \(\mathscr {B} \) can run the re-randomisation process backwards to recover the initial state. The proof of the following theorem can be found in the full version [14].
Theorem 3
Let \(\mathcal {E} = ({\mathsf {Key}}, \mathsf {Enc}, \mathsf {Rand} , \mathsf {Rand^{-1}} , \mathsf {Dec})\) be a \((t, q, \delta , \nu )\)- secure reverse re-randomizable encryption scheme, and suppose that \({\mathsf {PRG}} ^\prime = ({\mathsf {setup}} ^\prime , {\mathsf {init}} ^\prime , {\mathsf {next}} ^\prime )\) is a \((t, q, \epsilon _{fwd})\)-secure \(\mathrm {PRG}\). Then \({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) as defined in Fig. 8 is a \((t^\prime , q, 6\delta + 2\epsilon _{{fwd}} + q(q+3)\nu /2, ({{\textsf {first}}} , 1))\)-\(\mathrm {FWD}\)secure \(\mathrm {BPRG}\), where \(t^\prime \approx t\).
secure reverse re-randomizable encryption scheme, and suppose that \({\mathsf {PRG}} ^\prime = ({\mathsf {setup}} ^\prime , {\mathsf {init}} ^\prime , {\mathsf {next}} ^\prime )\) is a \((t, q, \epsilon _{fwd})\)-secure \(\mathrm {PRG}\). Then \({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) as defined in Fig. 8 is a \((t^\prime , q, 6\delta + 2\epsilon _{{fwd}} + q(q+3)\nu /2, ({{\textsf {first}}} , 1))\)-\(\mathrm {FWD}\)secure \(\mathrm {BPRG}\), where \(t^\prime \approx t\).
Construction of a forward-secure \(\mathrm {BPRG}\) \(({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} , \mathscr {B} )\) from a \((t, q, \delta , \nu )\)-reverse-re-randomizable  -secure PKE scheme \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) and a forward-secure \(\mathrm {PRG}\) \({\mathsf {PRG}} ^\prime = ({\mathsf {setup}} ^\prime , {\mathsf {init}} ^\prime , {\mathsf {next}} ^\prime )\).
-secure PKE scheme \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) and a forward-secure \(\mathrm {PRG}\) \({\mathsf {PRG}} ^\prime = ({\mathsf {setup}} ^\prime , {\mathsf {init}} ^\prime , {\mathsf {next}} ^\prime )\).
4 Backdooring PRNGs with Input
In this section, we address the second main theme in our paper: backdooring of PRNGs with input. To begin with, we show a simple construction for a PRNG with input that is both robust and subject to a limited form of backdooring: given a single output, \(\mathscr {B} \) can recover the state and all outputs back to the previous \({\mathsf {refresh}}\) and up to the next \({\mathsf {refresh}}\) operations (see Sect. 4.1). We then move on to provide our formal definition for backdoored PRNGs with input (BPRNGs) in Sect. 4.2; this definition demands much more of \(\mathscr {B} \), asking him to compute outputs beyond \({\mathsf {refresh}}\) operations, at the same time as asking that the BPRNG remain robust. Finally, in Sect. 4.3, we give a construction for a BPRNG meeting our backdooring notion for PRNGs with input, with various extensions to this construction being described in Sect. 4.4.
4.1 A Simple Backdoored PRNG
Let \({\mathsf {PRNG}} = ({\mathsf {setup}}, {\mathsf {init}}, {\mathsf {refresh}}, {\mathsf {next}})\) be a \(\mathrm {ROB}\)-secure \(\mathrm {PRNG}\) with input. By considering the special case of \(\mathsf {Game}\) \(\mathrm {ROB} ^{\mathscr {D},\mathscr {A}}_{{\mathsf {PRNG}},\gamma ^*}\) in which the adversary \(\mathscr {A}\) makes no \({\textsc {Set}} \) or \({\textsc {Ref}} \) calls, and one \({\textsc {Get}} \) call at the conclusion of the game, it is straightforward to see that \({\mathsf {PRG}} = ({\mathsf {setup}}, {\mathsf {init}}, {\mathsf {next}})\) must be a \(\mathrm {FWD}\)-secure \(\mathrm {PRG}\). This suggests that in order to backdoor \({\mathsf {PRNG}} \), we might try to replace \({\mathsf {PRG}} \) with a \(\mathrm {BPRG}\). As long as this implicit \(\mathrm {BPRG}\) is running without any refreshes, this should enable \(\mathscr {B} \) to carry out backdooring.
To make this idea concrete, we present in Fig. 9 a construction of a \(\mathrm {ROB}\)-secure PRNG with input from a PRG \({\mathsf {PRG}} \). This scheme is closely based on the PRNG with input from [17]. It utilises an online-computable extractor and a \(\mathrm {FWD}\)-secure \(\mathrm {PRG}\); our main modification is to ensure that repeated \({\mathsf {next}}\) calls are processed via a repeated iteration of a \(\mathrm {FWD}\)-secure \(\mathrm {PRG}\). A proof of robustness for this PRNG with input is easily derived from that of the original construction:
Lemma 1
Let \(\mathsf {Ext}: \{0,1\}^* \times \{0,1\}^v \rightarrow \{0,1\}^n\) be an online-computable \((\gamma ^*, \epsilon _{ext})\)-extractor. Let \({\mathsf {PRG}} = ({\mathsf {setup}} , {\mathsf {init}} , {\mathsf {next}} )\) be a \((t, q, \epsilon _{prg})\)-\(\mathrm {PRG}\) such that \(s _0 \twoheadleftarrow {\mathsf {init}} (pp)\) is equivalent to \(s _0 \twoheadleftarrow \{0,1\}^n\). Then \({\mathsf {PRNG}} = (\overline{{\mathsf {setup}}}, \overline{{\mathsf {init}}}, \overline{{\mathsf {refresh}}}, \overline{{\mathsf {next}}})\) as shown in Fig. 9 is a \(((t^\prime , q_r, q_n, q_c), \gamma ^*, q_n (2\epsilon _{prg}+q_r ^2\epsilon _{ext} +2^{-n+1}))\)-robust PRNG with input, where \(t^\prime \approx t\).
We now simply substitute a \(\mathrm {FWD}\)-secure \(\mathrm {BPRG}\) (such as that presented in Theorem 2) for \({\mathsf {PRG}} \) in this construction. Now, during the period between any pair of \({\mathsf {refresh}}\) calls in which the \(\mathrm {PRNG}\) is producing output, we inherit the backdooring advantage of the \(\mathrm {BPRG}\) in the new construction. However, the effectiveness of this backdoor is highly limited: as soon as \({\mathsf {refresh}}\) is called, the state of the \(\mathrm {PRNG}\) is refreshed with inputs, which, if of sufficiently high entropy, will make the state information-theoretically unpredictable. Then \(\mathscr {B} \) would need to compromise more output in order to regain his backdooring advantage.
One implication of this construction is that it makes it clear that, when considering stronger forms of backdooring, we must turn our attention to subverting \({\mathsf {refresh}}\) calls in some way.
Construction of a robust \(\mathrm {PRNG}\) \({\mathsf {PRNG}}\) from a \(\mathrm {FWD}\)-secure \(\mathrm {PRG}\) \({\mathsf {PRG}}\), based on [17].
4.2 Formal Definition for Backdoored PRNGs with Input
To make our backdooring models for \(\mathrm {PRNG}\)s with input as strong as possible, we wish to make minimal assumptions about Big Brother’s influence, whilst allowing the non-backdoored adversary \(\mathscr {A}\), to whom the backdoored schemes must still appear secure, maximum power to compromise the scheme. To this end, we will model \(\mathscr {B} \) as a passive observer who is able to capture just one \(\mathrm {PRNG}\) output, which he is then challenged to exploit. Simultaneously, we demand that the scheme is still secure in the face of a \(\mathrm {ROB}\)-adversary \(\mathscr {A}\), with all the capabilities this allows. Notably, the latter condition also offers the benefit of allowing us to explore the extent to which a guarantee of robustness may act as an immuniser against backdooring.
In our models to follow, we do not allow \(\mathscr {B} \) any degree of compromise over the distribution sampler \(\mathscr {D}\). This is again to fit with our ethos of making minimal assumptions on \(\mathscr {B} \)’s capabilities. It strengthens the backdooring model by demanding that the backdoor be effective against all samplers \(\mathscr {D}\) valid up to \(q_r\) samples, including in particular those not under the control of \(\mathscr {B} \). We also note that, in the extreme case where \(\mathscr {B} \) has complete knowledge of all the inputs used in \({\mathsf {refresh}}\) calls, then \(\mathscr {B} \)’s view of the evolution of the state is deterministic and the \(\mathrm {PRNG}\) is reduced to a \(\mathrm {FWD}\)-secure \(\mathrm {PRG}\) which is periodically reseeded with correlated values. Thus this restriction on Big Brother’s power ensures a clear separation between the results of Sect. 3 and those which follow.
Next consider a \(\mathrm {PRNG}\) with input which produces its output via a sequence of \({\mathsf {refresh}}\) and \({\mathsf {next}}\) calls. The evolution of the state, and subsequent production of output, is determined not only by the number of such calls, but also by their position in the sequence. To reflect this, each backdooring game below will take as input the specific refresh pattern rp which was used to produce the challenge. In line with this, and to reflect the fact that the refresh pattern may impact \(\mathscr {B} \)’s ability to subvert the scheme, the advantage of \(\mathscr {B} \) in our formal definition will be allowed to depend on the refresh pattern \({{\varvec{rp}}}\).
We present two new backdooring models for \(\mathrm {PRNG}\)s with input in Fig. 10. In the first game, the \(\mathrm {PRNG}\) is evolved according to the specified refresh pattern. Big Brother is given an output \(r _i\), and challenged to recover state \(s _j\). In the second game, Big Brother is again given output \(r _i\), but now we ask him to recover a different output value \(r _j\). In both games, Big Brother is additionally given the refresh pattern. Stronger notions can be achieved by considering games in which Big Brother is not given the refresh pattern, but for simplicity, we will consider the games shown in Fig. 10. In Sect. 4.4 we will discuss how our concrete construction of a BPRNG presented in Sect. 4.3 can be extended to the stronger setting in which Big Brother is not given the used refresh pattern. As with the corresponding \(\mathrm {PRG}\) definitions in Sect. 3.1, a BPRNG backdoored in the state sense is strictly stronger than one backdoored in the out sense.
Definition 21
A tuple of algorithms \({\overline{{\mathsf {PRNG}}}}\) = (\({\mathsf {setup}}\), \({\mathsf {init}}\), \({\mathsf {next}}\), \({\mathsf {refresh}}\), \(\mathscr {B}\)) is said to be a \((t, q_r, q_n, q_c, \gamma ^*, \epsilon , ({\textsf {type}}, \delta ))\)-robust BPRNG, where \({\textsf {type}} \in \{\textsf {state}, \textsf {out}\}\), if
-
\({\mathsf {PRNG}} = ({\mathsf {setup}}, {\mathsf {init}}, {\mathsf {refresh}}, {\mathsf {next}})\) is a \((t, q_r, q_n, q_c, \gamma ^*, \epsilon )\)-robust \(\mathrm {PRNG}\) with input;
-
For all refresh patterns \({{\varvec{rp}}} = (a_1,b_1,\ldots ,a_\rho ,b_\rho )\), where \(a_i,b_i,n\) are polynomial in the security parameter, for all distribution samplers \(\mathscr {D}\), for all \(1 \le i, j \le \sum _{\nu =1}^\rho a_\nu \), where \(i \ne j\), it holds that
 where
where 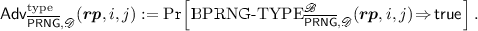
We note that by replacing the index j with a vector of indices \((j_1, \dots , j_k)\), we can immediately extend both of the above games to challenge Big Brother to recover multiple outputs and states.
4.3 Backdoored PRNG Construction
In Fig. 11, we present our construction of a BPRNG. The construction makes use of an ordinary non-backdoored PRNG with input, \({\mathsf {PRNG}}\), and is based on the simple idea of interleaving outputs of \({\mathsf {PRNG}}\) with encryptions of snapshots of the state of \({\mathsf {PRNG}}\), using an IND$-CPA secure encryption scheme. By taking a snapshot of the state whenever this is refreshed and storing a list of the previous k snapshots, the construction will enable \(\mathscr {B}\) to recover, with reasonable probability, the previous output values that were computed up to k refreshes ago. Of course, this means that the state of the final construction is large compared to that of the PRNG with input used as a component in its construction.
More specifically, the construction maintains a list of ciphertexts, \((C_{1},\ldots ,C_{k})\), encrypting k snapshots of the state of \({\mathsf {PRNG}}\). A snapshot of the state is taken in the \({\mathsf {\overline{next}}}\) algorithm of our construction, whenever the previous operation was a refresh. This ensures that if the state is successively refreshed multiple times, only a single snapshot will be stored. To produce an output value, the construction will use the \({\mathsf {next}}\) function of \({\mathsf {PRNG}}\) to compute a seed \(r \) which will either be used to directly compute an output value \(\overline{r}\) via a pair of PRGs, or used to re-randomize \((C_{1},\ldots ,C_{k})\), which will then be used as \(\overline{r}\). The combination of the IND$-CPA-security of the encryption scheme and the re-randomization will ensure that the output value in the latter case will remain pseudorandom to a regular PRNG adversary. Which of the two different output values the construction will produce is decided based on the seed \(r \).
We prove robustness of the generator by going via preserving and recovering security. To be able to achieve these notions, the ciphertexts \((C_{1},\ldots ,C_{k})\) are re-randomized a second time in \({\mathsf {\overline{next}}}\) to ensure that the overall state returned by \({\mathsf {\overline{next}}}\) appears independent of the output value \(\overline{r}\). Furthermore, to ensure recovering security, in which the adversary is allowed to maliciously set the state, the construction requires that the validity of ciphertexts can be verified. In particular, we assume the used encryption scheme is equipped with an additional algorithm, \(\textsf {invalid} \), which given a public key \(pk\) and a ciphertext \( C\) , returns 1 if \( C\) is invalid for \(pk\), and 0 if it is valid. This is used to ensure that the state of the construction always contains valid ciphertexts. Additionally, we require the used encryption scheme to satisfy a stronger re-randomization property than was introduced in Sect. 2: the re-randomisation of an adversarially chosen ciphertext should be indistinguishable from the encryption of any message. We will formalize this property below.
For the Big Brother algorithm \(\mathscr {B} \) in the construction to be successful, it is required that the output value \(\overline{r}_i\) given to \(\mathscr {B} \) corresponds to \((C_{1},\ldots ,C_{k})\), and that the output value \(\overline{r}_j\) that \(\mathscr {B} \) is required to recover corresponds to a value computed directly from the then current state of \({\mathsf {PRNG}}\). Since the type of the produced output is decided from the output of \({\mathsf {PRNG}}\) and a PRG which are both assumed to be good generators, this will happen with probability close to 1/4. Furthermore, it is required that the number of refresh periods between \(\overline{r}_j\) and \(\overline{r}_i\) is less than k. More precisely, for a refresh pattern \({{\varvec{rp}}} = (a_1,b_1,\ldots ,a_\rho ,b_\rho )\), the number of refresh periods \({\mathsf {PRNG}}\) has undergone when \(\overline{r}_i\) and \(\overline{r}_j\) are produced, are \(i_{ref} = \max _{\sigma }[ \sum _{\nu = 1}^\sigma a_\nu < i]\) and \(j_{ref} = \max _{\sigma } [\sum _{\nu = 1}^\sigma a_\nu < j]\), respectively. If \(i_{ref} - j_{ref} < k\), the initial refreshed state used to compute \(\overline{r}_j\) will be encrypted in \(C_{i_{ref} - j_{ref} + 1}\). Hence, all \(\mathscr {B} \) has to do is to decrypt and iterate this state \(j_{it} = j - \sum _{\nu = 1}^{j_{ref}} a_\nu \) times to obtain the seed used to compute \(\overline{r}_j\).
The full construction, shown in Fig. 11, is based on a (non-backdoored) (n, l, p)-PRNG with input, \({\mathsf {PRNG}} = ({\mathsf {setup}},{\mathsf {init}},{\mathsf {refresh}},{\mathsf {next}})\), a pair of PRGs \({\mathsf {PRG}}: \{0,1\}^l \rightarrow \{0,1\}^{2ku+ 1}\) and \({\mathsf {PRG}} ': \{0,1\}^u\rightarrow \{0,1\}^{k \times m}\), and a re-randomizable encryption scheme \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Rand}, \mathsf {Dec}, \textsf {invalid})\) with message space \(\{0,1\}^{n}\), randomness space \(\{0,1\}^u\), and ciphertext space \(\{0,1\}^m\), and produces a \((k \times m + n + 1, k \times m, p)\)-PRNG with input.
Before proving the construction to be robust and backdoored, we formalize the stronger re-randomization property mentioned above. Note that this property is not comparable to the re-randomization definition for PKE given in Sect. 2: that was a statistical notion concerning encryptions of the same message, while, in contrast, the following is a computational notion regarding possibly different messages.
Definition 22
An encryption scheme \(\mathcal {E} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) with message space \(\{0,1\}^{n}\) is said to be \((t,\delta )\)-strongly re-randomizable, if there exists a polynomial time algorithm \(\mathsf {Rand}\) such that
-
For all \((pk,sk) \leftarrow \mathsf {KGen}\), \(M \in \{0,1\}^{n}\), and \(c \leftarrow \mathsf {Enc}(pk, M)\), it holds that
$$\begin{aligned} \Pr [\mathsf {Dec}_{sk}(\mathsf {Rand}(C)) = M ] = 1. \end{aligned}$$ -
For all adversaries \(\mathscr {A}\) with running time t and for all messages \(M \in \{0,1\}^{n}\), it holds that
 , where
, where 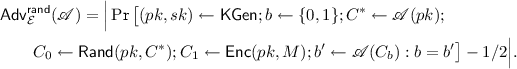
In the above, it is required that the output \(C ^*\) of \(\mathscr {A}\) is a valid ciphertext under \(pk\).
It is relatively straightforward to see that ElGamal encryption satisfies the above re-randomization property. Specifically, for a public key \(y = g^x\) and a ciphertext \(C = (C ^1,C ^2) = (g^r,M \cdot y^r)\), a re-randomization \(C _0\) of \(C \) is obtained by picking random \(r^\prime \) and computing \(C _0 = (C ^1 \cdot g^{r'}, C ^2 \cdot y^{r'})\). However, under the DDH assumption, the tuples \((g,g^{r'},y,y^{r'})\) and \((g,g^{r'},y,z)\) are indistinguishable, where z is a random group element. Hence, re-randomization of \(C \) is indistinguishable from multiplying the components of \(C \) with random group elements, which again makes \(C _0\) indistinguishable from two random group elements. Likewise, the encryption of any message \(M \), \(C _1 = (g^r, M \cdot y^r)\), is indistinguishable from two random group elements under the DDH assumption, which makes \(C _0\) and \(C _1\) indistinguishable.
The proof of the following theorem appears in the full version [14].
Theorem 4
Let \({\mathsf {PRG}}\) and \({\mathsf {PRG}} ^\prime \) be \(\epsilon _{prg}\)-secure and \(\epsilon ^\prime _{prg}\)-secure PRGs respectively, and let \({\mathsf {PRNG}}\) be a \((t,\epsilon _{pre})\)-\(\mathrm {PRE}\)and \((t,q_r,\gamma ^*,\epsilon _{rec})\)-\(\mathrm {REC}\)secure PRNG with input. Suppose further that \(\mathcal {E}\) is a \((t,q_{ind},\epsilon _{ind})\)- secure and \((t, \epsilon _{rand})\)-strongly re-randomizable encryption scheme. Then \({\overline{{\mathsf {PRNG}}}} \) shown in Fig. 11 is a \((t^\prime ,q_r,q_n,q_c,\gamma ^*,\epsilon ,(\textsf {out},\delta ))\)-robust BPRNG, where \(t^\prime \approx t\),
secure and \((t, \epsilon _{rand})\)-strongly re-randomizable encryption scheme. Then \({\overline{{\mathsf {PRNG}}}} \) shown in Fig. 11 is a \((t^\prime ,q_r,q_n,q_c,\gamma ^*,\epsilon ,(\textsf {out},\delta ))\)-robust BPRNG, where \(t^\prime \approx t\),
and
where \({{\varvec{rp}}} = (a_1,b_1,\ldots ,a_\rho ,b_\rho )\), \(a = \sum _{\nu =1}^\rho a_\nu \), \(i_{ref} \leftarrow \max _\sigma \left[ \textstyle \sum _{\nu = 1}^\sigma a_\nu < i \right] \), and \(j_{ref} \leftarrow \max _\sigma \left[ \textstyle \sum _{\nu = 1}^\sigma a_\nu < j \right] \).
Construction of a robust BPRNG using as components a re-randomisable PKE scheme \(\mathcal {E}\) = (\(\mathsf {KGen}\), \(\mathsf {Enc}\), \(\mathsf {Dec}\), \(\mathsf {Rand}\), \(\textsf {invalid}\)), a PRNG with input \({\mathsf {PRNG}} = ({\mathsf {setup}},{\mathsf {init}},{\mathsf {refresh}},{\mathsf {next}})\), and PRGs \({\mathsf {PRG}} \) and \({\mathsf {PRG}} '\).
4.4 Extensions and Modifications of Our Main Construction
The above construction can be modified and extended to provide slightly different properties. For example, an alternative to storing a snapshot of a refreshed state by rotating the ciphertexts \((C_{1},\ldots ,C_{k})\) as done in line 9 of \({\mathsf {\overline{next}}}\), would be to choose a random ciphertext to replace. More specifically, the output value \(r \) of \({\mathsf {PRNG}}\) computed in line 7 could be stretched to produce a \(\log k\) bit value t, and ciphertext \(C_{t}\) would then be replaced with \(C_{0}\). Note, however, that \(\mathscr {B} \) would no longer be able to tell which ciphertext corresponds to which snapshot of the state. This can be addressed if the used encryption scheme is additionally assumed to be additively homomorphic, e.g. like ElGamal encryption, which, using an appropriate group, also satisfies all of the other requirements of the construction. In this case, the construction would be able to maintain an encrypted counter of the number of refresh periods, and, for each snapshot, store an encrypted value corresponding to the number of refresh periods \({\mathsf {PRNG}}\) has undergone before the snapshot was taken. If the ciphertexts containing these values are concatenated with \((C_{1},\ldots ,C_{k})\) to produce the output value \(\overline{r}\), then \(\mathscr {B} \) obtains sufficient information to derive what state to use to recover a given output value. This yields a construction with slightly different advantage function \(\delta ({{\varvec{rp}}},i,j)\) compared to the above construction; instead of a sharp drop to 0 when i and j are separated by k refresh periods, the advantage gradually declines as the distance (in terms of the number of refresh periods) between i and j increases.
The above construction can furthermore be modified to produce shorter output values. Specifically, instead of setting \(\overline{r} \leftarrow (C_{1},\ldots ,C_{k})\) in line 16 of \({\mathsf {\overline{next}}}\), a random ciphertext \(C_{t}\) could be chosen as \(\overline{r}\), by stretching the output of \({\mathsf {PRG}}\) in line 11 with an additional \(\log k\) bits to produce t. This will reduce the output length from km bits to m bits. However, a similar problem to the above occurs: \(\mathscr {B} \) will not be able to tell which snapshot \(C_{t}\) represents. Using a similar solution to the above will increase the output length to 2m bits. This modification will essentially reduce the backdooring advantage by a factor of 1 / k compared to the above construction.
Lastly, we note that the above construction assumes \(\mathscr {B} \) receives as input the refresh pattern \({{\varvec{rp}}}\). Again, by maintaining encrypted counters for both the number of refresh periods and the number of produced output values for each snapshot, we can obtain an algorithm \(\mathscr {B} \) which does not require \({{\varvec{rp}}}\) as input, but at the cost of increasing the output size.
All of the above modifications can be shown to be secure using almost identical arguments to the existing security analysis for the above construction.
5 On the Inherent Resistance of PRNGs with Input to Backdoors
In the previous section we have shown a construction, and variations thereof, for a PRNG with input that is backdoored in a powerful sense: from a given output Big Brother can recover prior state and output values past an arbitrary number of refreshes. One can see however that in our constructions, Big Brother’s ability to go past refreshes is limited by the size of the state and output of the constructed generator. We now show that this limitation is inherent in any PRNG with input that is robust.
In particular consider the sequence representing the evolution of a PRNG’s state, and select a subsequence of states where any two states are separated by consecutive refreshes that in combination have high entropy. Then we will show that the number of such states that Big Brother can predict simultaneously with non-negligible probability is limited by the size of the state. Thus if we limit the state size of a robust PRNG, then Big Brother’s ability in exploiting any potential backdoors that it may contain must decrease as more entropy becomes available to the PRNG.
5.1 An Impossibility Result
We now turn to formalising the preceding claim. In order to simplify the analysis to follow, we focus on a restricted class of distribution samplers. We say that a distribution sampler is well-behaved if it satisfies the following properties:
-
It is efficiently sampleable.
-
For any i the entropy estimate \(\gamma _i\) of the random variable \(I_i\) is fixed, but may vary across different values of i.
-
For all \(i>0\) such that \(\Pr (\sigma _{i-1})>0\) it holds that:
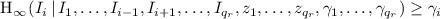
where \((\sigma _i,I_i,\gamma _i,z_i)=\mathscr {D} (\sigma _{i-1})\) for \(i\in \{1,\dots ,q_r \}\) and \(\sigma _0=\varepsilon \).
For any well-behaved distribution sampler \(\mathscr {D}\) and any PRNG with input \({\mathsf {PRNG}}\), let us now consider the experiment of running \({\mathsf {setup}}\) and \({\mathsf {init}}\) to obtain a public paramer \(pp\) and an initial state \(S _0\), and then applying a sequence of queries \(q_1,\dots ,q_i,\ldots \) where each \(q_i\) represents a query to \({\mathsf {refresh}} \) or \({\mathsf {next}} \). To any query \(q_i\) we associate a tuple \((R _i,S _i,\sigma _i,I_i,\gamma _i)\) that represents the outcome of that query. If \(q_i\) is a \({\mathsf {refresh}}\) query these variables are set by the outputs of \(\mathscr {D}\) and \({\mathsf {refresh}} \), while \(R _i\) is set to \(\varepsilon \). If \(q_i\) is a \({\mathsf {next}}\) query these variables are set to the outputs of \({\mathsf {next}} \) while \(\gamma _i\) is set to zero, \(I_i\) is set to the empty string, and \(\sigma _i\leftarrow \sigma _{i-1}\). (Note that we deviate slightly here in the notation we use for the output and state of a PRNG with input: we use \(R _i\) and \(S _i\) to denote random variables and we use \(r_i\) and \(s_i\) respectively to denote values assumed by these random variables.)
Now let the function \(f:\mathbb {N}\rightarrow \mathbb {N}\) where \(f (0)=0\) identify a subsequence \((R _{f (j)},S _{f (j)},\sigma _{f (j)},I_{f (j)},\gamma _{f (j)})\). We say that a subsequence is legitimate if for all \(S _{f (j)}\) there exists \(f (j-1)\le c\le d\le f (j)\) such that \(\sum _c^d \gamma _i \ge \gamma ^* \), and all queries between c and d are refresh queries. For ease of notation we let \(\epsilon \) denote an upper bound on  over all \(\mathscr {D} ^{\prime } \) and all \(\mathscr {A} \) in some class of adversaries with restricted sources.
over all \(\mathscr {D} ^{\prime } \) and all \(\mathscr {A} \) in some class of adversaries with restricted sources.
With this notation established, we can state the main theorem of this section as follows:
Theorem 5
For any PRNG with input \({\mathsf {PRNG}}\) having associated parameters (n, l, p), any well-behaved distribution sampler \(\mathscr {D}\), any sequence of queries, any legitimate subsequence identified by the function \(f \), any index j, and any \(k\in \mathbb {N}\), it holds that:

The proof of the theorem can be found in the full version [14].
This theorem deserves some interpretation. On the left-hand-side, \(R _{f (j)+k}\) refers to a particular output received by \(\mathscr {B} \) and \(pp \) to the public parameters. The theorem says that, conditioned on these, the vector of states \(\bar{S '}_{f (j)}\) still has large average min-entropy, provided j is sufficiently large. This is because, on the right-hand-side, \(\min (n,l)\) is fixed for a given generator, \(\epsilon \) is small (so \(\log \left( \frac{1}{\epsilon }\right) \) is large), and the first term scales linearly with j, thus attaining arbitrarily large values as j increases. This means that it is impossible for \(\mathscr {B} \) to compute or guess the state vector with a good success probability. In short, no adversary, irrespective of its computational resources or backdoor information, can recover all the state information represented by the vector \(\bar{S '}_{f (j)}\). In addition the result extends easily to the stronger setting where the adversary is given any sequence of outputs following \(R _{f (j)}\), since these will depend only on \(S _{f (j)}\) and independently sampled future I values. In that case, we simply replace the \(R _{f (j)+k}\) term by any sequence of ouputs following \(R _{f (j)}\) and \(\min (n,l)\) by n.
5.2 Discussion and Open Problems
Theorem 5 concerns state recovery attacks against robust PRNGs with input. It seems plausible to us that the result can be strengthened to say something about the impossibility of recovering old outputs, instead of old states. Likewise, the theorem only concerns the impossibility of recovering old states from current outputs, but nothing about the hardness of recovering future states or outputs (after refreshing) from current outputs. Informally, the strength of the robustness security notion seems to make such a result plausible, since it essentially requires that a PRNG with input cannot ignore its entropy inputs when refreshing. However, we have not yet proved a formal result in this direction. These are problems that we intend to study in our immediate future work. They relate closely to the kind of impossibility result that would be useful in demonstrating the absence of the kind of effective backdooring that \(\mathscr {B} \) might prefer to perform.
This result can also be seen as saying that a PRNG with input is, to some extent, intrinsically immunised against backdooring attacks, since \(\mathscr {B} \) cannot recover all old states once sufficient entropy has been accumulated in the generator. Here the immunisation is a direct consequence of the nature of the primitive. By contrast, for PRGs, the results of [15] concerning immunisation of PRGs require intrusive changes to the PRG, essentially post-processing the generator’s output with either a keyed primitive (a PRF) or a hash with relatively strong security (a random oracle or a Universal Computational Extractor). Moreover, our strengthening of the result of [15], via constructions of forward-secure PRGs that are backdoored in the strong \({{\textsf {first}}}\) sense, shows that PRGs cannot resist backdooring in general. So some form of external immunisation is inevitable if PRGs are to resist backdooring.
On the other hand, exploring immunisation for PRNGs with input would still be useful, since, as our constructions in Sect. 4 show, it is possible to achieve meaningful levels of backdooring for PRNGs with input. Naively, the immunisation techniques of [15] should work equally well for PRNGs with input as they do for PRGs, since a PRNG with input certainly contains within it an implicit PRG, and if that simpler component is immunised, then so should be the more complex PRNG primitive. Furthermore, it may be that PRNGs with input, being informally harder to backdoor, could be immunised by applying less intrusive or less idealised cryptographic techniques.
Notes
- 1.
See for example https://en.wikipedia.org/wiki/RdRand for a description of Intel’s “Bull Mountain” random number generator.
- 2.
See for example http://www.realworldcrypto.com/rwc2016/program/rwc16-shacham.pdf?attredirects=0&d=1 for the Dual EC DRBG being used as a backdoor in Juniper networking equipment; see also http://www.theguardian.com/world/2013/sep/05/nsa-gchq-encryption-codes-security for the original reporting on project Bullrun.
References
Abeni, P., Bello, L., Bertacchini, M.: Exploiting DSA-1571: How to break PFS in SSL with EDH, July 2008
Ateniese, G., Magri, B., Venturi, D.: Subversion-resilient signature schemes. Cryptology ePrint Archive, Report 2015/517 (2015). http://eprint.iacr.org/2015/517
Baignères, T., Delerablée, C., Finiasz, M., Goubin, L., Lepoint, T., Rivain, M.: Trap me if you can - million dollar curve. IACR Cryptology ePrint Archive 2015:1249 (2015)
Barak, B., Halevi, S.: A model and architecture for pseudo-random generation with applications to/dev/random. In: Atluri, V., Meadows, C., Juels, A. (eds.) ACM CCS 05, Alexandria, Virginia, USA, 7–11 November 2005, pp. 203–212. ACM Press (2005)
Bellare, M., Boldyreva, A., O’Neill, A.: Deterministic and efficiently searchable encryption. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 535–552. Springer, Heidelberg (2007)
Bellare, M., Paterson, K.G., Rogaway, P.: Security of symmetric encryption against mass surveillance. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 1–19. Springer, Heidelberg (2014)
Bernstein, D.J., Chang, Y.-A., Cheng, C.-M., Chou, L.-P., Heninger, N., Lange, T., van Someren, N.: Factoring RSA keys from certified smart cards: coppersmith in the wild. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 341–360. Springer, Heidelberg (2013)
Bernstein, D.J., Chou, T., Chuengsatiansup, C., Hülsing, A., Lange, T., Niederhagen, R., van Vredendaal, C.: How to manipulate curve standards: a white paper for the black hat. Cryptology ePrint Archive, Report 2014/571 (2014). http://eprint.iacr.org/2014/571
Bernstein, D.J., Hamburg, M., Krasnova, A., Lange, T.: Elligator: elliptic-curve points indistinguishable from uniformrandom strings. In: Sadeghi, A.-R. et al. [29], pp. 967–980
Brown, D.R.L.: A weak-randomizer attack on RSA-OAEP with e = 3. Cryptology ePrint Archive, Report 2005/189 (2005). http://eprint.iacr.org/2005/189
Checkoway, S., Niederhagen, R., Everspaugh, A., Green, M., Lange, T., Ristenpart, T., Bernstein, D.J., Maskiewicz, J., Shacham, H., Fredrikson, M.: On the practical exploitability of dual EC in TLS implementations. In: Fu, K., Jung, J. (eds.) Proceedings of the 23rd USENIX Security Symposium, San Diego, CA, USA, 20–22 August 2014, pp. 319–335. USENIX Association (2014)
Cornejo, M., Ruhault, S.: Characterization of real-life PRNGs under partial state corruption. In: Ahn, G.-J., Yung, M., Li, N. (eds.) ACM CCS 14, Scottsdale, AZ, USA, 3–7 November 2014, pp. 1004–1015. ACM Press (2014)
Degabriele, J.P., Farshim, P., Poettering, B.: A more cautious approach to security against mass surveillance. In: Leander, G. (ed.) FSE 2015. LNCS, vol. 9054, pp. 579–598. Springer, Heidelberg (2015)
Degabriele, J.P., Paterson, K.G., Schuldt, J.C.N., Woodage, J.: Backdoors in pseudorandom number generators: possibility andimpossibility results. Cryptology ePrint Archive, Report 2016/577 (2016). http://eprint.iacr.org/2016/577
Dodis, Y., Ganesh, C., Golovnev, A., Juels, A., Ristenpart, T.: A formal treatment of backdoored pseudorandom generators. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 101–126. Springer, Heidelberg (2015)
Dodis, Y., Ong, S.J., Prabhakaran, M., Sahai, A.: On the (im)possibility of cryptography with imperfect randomness. In: 45th FOCS, Rome, Italy, 17–19 October 2004, pp. 196–205. IEEE Computer Society Press (2004)
Dodis, Y., Pointcheval, D., Ruhault, S., Vergnaud, D., Wichs, D.: Security analysis of pseudo-random number generators with input: /dev/random is not robust. In: Sadeghi, A.-R., et al. [29], pp. 647–658
Dodis, Y., Shamir, A., Stephens-Davidowitz, N., Wichs, D.: How to eat your entropy and have it too – optimal recovery strategies for compromised RNGs. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 37–54. Springer, Heidelberg (2014)
Goldberg, I., Wagner, D.: Randomness and the Netscape browser. Dr Dobb’s J.-Softw. Tools Prof. Programmer 21(1), 66–71 (1996)
Hemenway, B., Libert, B., Ostrovsky, R., Vergnaud, D.: Lossy encryption: constructions from general assumptions and efficient selective opening chosen ciphertext security. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 70–88. Springer, Heidelberg (2011)
Heninger, N., Durumeric, Z., Wustrow, E., Halderman, J.A.: Mining your Ps, Qs: detection of widespread weak keys in network devices. In: Kohno, T. (ed.) Proceedings of the 21th USENIX Security Symposium, Bellevue, WA, USA, 8–10 August 2012, pp. 205–220. USENIX Association (2012)
Lenstra, A.K., Hughes, J.P., Augier, M., Bos, J.W., Kleinjung, T., Wachter, C.: Public keys. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 626–642. Springer, Heidelberg (2012)
Mironov, I., Stephens-Davidowitz, N.: Cryptographic reverse firewalls. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 657–686. Springer, Heidelberg (2015)
Möller, B.: A public-key encryption scheme with pseudo-random ciphertexts. In: Samarati, P., Ryan, P.Y.A., Gollmann, D., Molva, R. (eds.) ESORICS 2004. LNCS, vol. 3193, pp. 335–351. Springer, Heidelberg (2004)
Mueller, M.: Debian OpenSSL predictable PRNG bruteforce SSH exploit, May 2008
Peikert, C., Waters, B.: Lossy trapdoor functions and their applications. In: Ladner, R.E., Dwork, C. (eds.) 40th ACM STOC, Victoria, British Columbia, Canada, 17–20 May 2008, pp. 187–196. ACM Press (2008)
Ristenpart, T., Yilek, S.: When good randomness goes bad: virtual machine reset vulnerabilities and hedging deployed cryptography. In: Proceedings of the Network and Distributed System Security Symposium, NDSS 2010, San Diego, California, USA, 28 February–3 March 2010. The Internet Society (2010)
Russell, A., Tang, Q., Yung, M., Zhou, H.-S.: Cliptography: clipping the power of kleptographic attacks. Cryptology ePrint Archive, Report 2015/695 (2015). http://eprint.iacr.org/2015/695
Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 13, Berlin, Germany, 4–8 November 2013. ACM Press (2013)
Shumow, D., Ferguson, N.: On the possibility of a back door in the NIST SP800-90 Dual EC PRNG. Presentation at rump session of CRYPTO 2007 (2007)
Simmons, G.J.: The prisoners’ problem and the subliminal channel. In: Chaum, D. (ed.) CRYPTO 1983, Santa Barbara, CA, USA, pp. 51–67. Plenum Press, New York (1983)
Vazirani, U.V., Vazirani, V.V.: Trapdoor pseudo-random number generators, with applications to protocol design. In: 24th Annual Symposium on Foundations of Computer Science, Tucson, Arizona, USA, 7–9 November 1983, pp. 23–30. IEEE Computer Society (1983)
Yilek, S., Rescorla, E., Shacham, H., Enright, B., Savage, S., When private keys are public: results from the 2008 Debian OpenSSL vulnerability. In: Feldmann, A., Mathy, L. (eds.) Proceedings of the 9th ACM SIGCOMM Internet Measurement Conference, IMC 2009, Chicago, Illinois, USA, 4–6 November 2009, pp. 15–27. ACM (2009)
Young, A., Yung, M.: Kleptography: using cryptography against cryptography. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 62–74. Springer, Heidelberg (1997)
Young, A., Yung, M.: Relationships between Diffie-Hellman and “index oracles”. In: Blundo, C., Cimato, S. (eds.) SCN 2004. LNCS, vol. 3352, pp. 16–32. Springer, Heidelberg (2005)
Acknowledgments
Degabriele and Paterson were supported by EPSRC grant EP/M013472/1 (UK Quantum Technology Hub for Quantum Communications Technologies). Schuldt was supported by JSPS KAKENHI Grant Number 15K16006. Woodage was supported by the EPSRC and the UK government as part of the Centre for Doctoral Training in Cyber Security at Royal Holloway, University of London (EP/K035584/1)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Degabriele, J.P., Paterson, K.G., Schuldt, J.C.N., Woodage, J. (2016). Backdoors in Pseudorandom Number Generators: Possibility and Impossibility Results. In: Robshaw, M., Katz, J. (eds) Advances in Cryptology – CRYPTO 2016. CRYPTO 2016. Lecture Notes in Computer Science(), vol 9814. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53018-4_15
Download citation
DOI: https://doi.org/10.1007/978-3-662-53018-4_15
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53017-7
Online ISBN: 978-3-662-53018-4
eBook Packages: Computer ScienceComputer Science (R0)





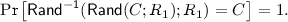

 and
and  .
.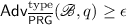 .
.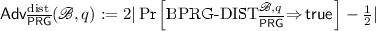 ,
,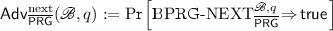 ,
,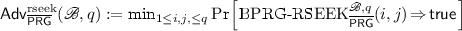 .
.
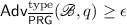 .
.


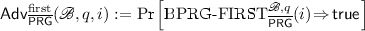 , and
, and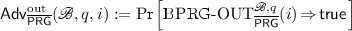

 and
and  .
.



 and
and  for BPRNGs.
for BPRNGs. where
where 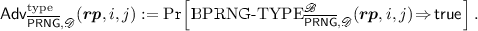
 , where
, where