Abstract
Non-Malleable Codes for the split state model allow to encode a message into two parts such that arbitrary independent tampering on the parts either destroys completely the content or maintains the message untouched. If the code is also leakage resilient it allows limited independent leakage from the two parts. We propose a model where the two parts can be refreshed independently. We give an abstract framework for building codes for this model, instantiate the construction under the external Diffie-Hellman assumption and give applications of such split-state refreshing. An advantage of our new model is that it allows arbitrarily many tamper attacks and arbitrarily large leakage over the life-time of the systems as long as occasionally each part of the code is refreshed. Our model also tolerates that the refreshing occasionally is leaky or tampered with.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Non-malleable codes (NMCs) are a natural relaxation of the notions of error correcting codes and error detecting codes, which tolerates more attacks by relaxing the security guarantees. An error correcting code guarantees that the encoded message is always correctly decoded. The price for this guarantee is that the code can tolerate only limited attacks, e.g., that some small constant fraction of the codeword is tampered with. An error detecting code decodes either the correct message or returns some special symbol \(\bot \) signalling an error. They can tolerate more general attacks, e.g., that some larger constant fraction of the codeword is tampered with. A NMC only guarantees that either the encoded message is correctly decoded or the decoder outputs a message which is unrelated to the encoded message. This weak guarantee allows much more general tampering. It is for instance possible to tolerate tampering that modifies the entire codeword.
Despite the weaker security guarantee, NMCs can be used to protect against physical attacks. Consider a physical device D with an embedded secret key K. For instance a signature card which on input m outputs \(\sigma = \mathsf {Sign}_K(m)\). Assume the device might fall into the hands of an adversary that can apply a physical attack on the device to tamper with K, producing a different but related key \(K'\). Now, on input m the device outputs \(\sigma = \mathsf {Sign}_{K'}(m)\). We would like to ensure that the adversary cannot learn any information about K from seeing \(\mathsf {Sign}_{K'}(m)\). Let \(\mathsf {Encode}\) and \(\mathsf {Decode}\) denote the encoding and decoding algorithms of a NMC. Consider now a device \(\tilde{D}\) on which we store an encoded key \(X \leftarrow \mathsf {Encode}(K)\). On input m the device outputs \(\sigma = \mathsf {Sign}_{\mathsf {Decode}(X)}(m)\). We call \(\tilde{D}\) the strengthened device. In face of a tampering with the key the strengthened device outputs \(\sigma = \mathsf {Sign}_{\mathsf {Decode}(X')}(m)\). The value of \(\mathsf {Decode}(X')\) will either be K or an unrelated key \(K'\). NMC security guarantees that when \(K'\) is an unrelated key, then the adversary could in fact have computed \(K'\) itself without any access to K. It follows that the adversary either learns a correct signature \(\sigma = \mathsf {Sign}_{K}(m)\) or a value \(\sigma = \mathsf {Sign}_{K'}(m)\) it could have computed itself without access to the device. This ensures that tampering does not result in information leaking from the device.
Formally security is defined as a tampering game between an adversary and a simulator \(\mathsf {S}\). The adversary submits to the tampering game a message m and the game computes a random encoding \(X \leftarrow \mathsf {Encode}(m)\). The adversary then submits a tampering function T. Now the game either computes \(m' = \mathsf {Decode}(T(X))\) and gives \(m'\) to the adversary. Or, it computes \(m' = \mathsf {S}(T)\) and gives \(m'\) to the adversary. The code is called secure if for all adversaries there exists an efficient simulator such that the adversary cannot guess which of the two cases occurred except with negligible advantage. A small but crucial modification of the game is needed. Notice that the adversary might for instance submit T equal to the identity function. In that case \(m' = m\) in the first case, so the simulator would be required to compute m too, which is impossible as it is not given m as input and m might be a random value. The game is therefore modified to allow \(\mathsf {S}\) to give a special output \(*\) in which case the game sets \(m' = m\) before giving \(m'\) to the adversary. Security therefore demonstrates that the adversary when submitting a tampering function T could itself efficiently have computed whether the tampering will have no effect (when \(\mathsf {S}(T) = *\)) and in case there is an effect, which message \(m' = \mathsf {S}(T)\) would be the result of the tampering.
It is clear that we need to put some restriction on the tampering function. If the adversary submits the function \(T(X) = \mathsf {Encode}(\mathsf {Decode}(X)+1)\) the simulator would have to output \(m+1\) without knowing m. The most popular way to restrict the tampering functions is to assume the split-state model (STM), which was first used to get leakage-resilient cryptography (see Dziembowski et al. [21]). In this model we assume that the encoding X consists of two parts \(X = (X^0, X^1)\) stored on two separate storage devices or separate parts of a chip. The assumption is that the adversary can only tamper independently with the two parts, i.e., in the model it submits tampering functions \(T = (T^0, T^1)\) and the result of tampering is \((X'^0, X'^1) = (T^0(X^0), T^1(X^1))\). This is also the model we consider in this paper. In the split state model it is possible to construct codes which tolerates arbitrary tampering, except that the two parts must be tampered independently.
Unfortunately NMC security is not sufficient for device strengthening if the adversary can repeatedly tamper with the device. To see this assume for simplicity that the encoding has the property that if a single bit is flipped in an encoding X, then \(\mathsf {Decode}(X') = \bot \). Consider then the tampering function \(O_i\) which overwrites the i’th bit in X by 0. Each \(O_i\) is allowed in the split-state model. Now, \(\mathsf {Decode}(O_i(X)) = \bot \) if and only if the i’th bit of X is 1. Hence by applying \(O_1, \ldots , O_{\vert X \vert }\) an adversary can learn X and then compute \(m = \mathsf {Decode}(X)\). This means that if the code is secure then by definition the simulator can also compute m, which it cannot. Let us call the above attack the fail-or-not attack.
Two different ways to circumvent the fail-or-not attack has been proposed in the literature. In [34] Liu and Lysyanskaya propose that the strengthened device whenever it reconstructed the key \(K = \mathsf {Decode}(X)\) resamples a new encoding \(X' \leftarrow \mathsf {Encode}(K)\) and overrides X by \(X'\) on the storage medium. This way the adversary gets to tamper with each fresh encoding only once and the NMC assumption is sufficient. In [25] Faust et al. propose a model where the encoding X remains the same in all tamperings. Instead the authors assume that the strengthened device self destructs when it detects that \(\mathsf {Decode}(X) = \bot \). In the fail-or-not attack the adversary is using failure or not to leak information on the encoding X. If the device self destructs on failure this can however only be exploited to leak logarithmic many bits, namely in which round of tampering the self destruction happened. The authors in [25] then use a code which can tolerate limited leakage on the two halves of the encoding and constructs the code such that computing in which round the device would have self-destructed can be done using only limited independent leakage from the two halves, reducing tampering to leakage, an idea we use in our new code too.
Both [25, 34] consider codes which are additionally leakage resilient in the split state model. In [25] this is needed anyway to protect against tampering and in [34] it is argued to be a natural requirement as we assume the device to be in the hands of an adversary which might learn leakage on the two parts \(X^0\) and \(X^1\) by measuring the device during operation. In both [25, 34] it is assumed that the circuitry doing the encoding (and refreshing) cannot be tampered with and that it is leakage free, i.e., only the storage devices are subject to tampering and leakage. Below we will partially relax this assumption by allowing occasional leakage and tampering of the refresh procedure.
Our Contributions We propose a new model in line with [34]. In particular we do not assume the device can self destruct and we use refreshing to protect against the fail-or-not attack. We propose two extra requirements on the refreshing which we motivate below. First, we want the refreshing to be split-state, i.e., the refreshing algorithm should be of the form \(\mathsf {Refresh}(X) = (\mathsf {Refresh}_0(X^0), \mathsf {Refresh}_1(X^1))\). Second, the code should tolerate multiple tampering attacks in between refreshes.
To motivate the model, imagine the following application for strengthening a device. The parts \(X^0\) and \(X^1\) are placed in separate storages. When the key is needed the device computes \(K = \mathsf {Decode}(X)\) and outputs \(\mathsf {Sign}_K(m)\). In addition to this, occasionally the device will read up a part \(X^i\) and write back \(X'^i = \mathsf {Refresh}(X^i)\). The refreshing of the parts might also be done by separate processes sitting in the storage device of the part, as opposed to the circuitry doing the decoding. The practical motivation is as follows. In all existing codes the encoding process is considerably more complex than the decoding process. For instance encoding necessarily needs cryptographic strength randomness, whereas decoding can be deterministic. It could therefore be much harder to create a leakage and tamper free implementation of \(\mathsf {Encode}\). Also, refreshing by decoding and re-encoding is unnecessarily risky as (real-world) leakage from this process could be leakage on the decoded key K.
Notice on the other hand that if a partial refreshing \(X'^i = \mathsf {Refresh}(X^i)\) is tampered with, then it can simply be considered just another tampering attack on \(X^i\) in the split state model. In the same way, if a partial refreshing \(X_i' = \mathsf {Refresh}(X_i)\) is leaky, then it can simply be considered just another leakage attack on \(X_i\) in the split state model. For this to be true it is important that the refreshing is split state, motivating our first extra requirement. As a consequence, if only occasionally the refreshing succeeds in being tamper and leakage free, all the failed attempts can be recast as tamper and leakage attacks. This means the code remains secure if it can tolerate several tamper and leakage attacks in between refreshes, motivating our second extra requirement. Notice that for this to be true, the security of the code should not depend on the two parts being refreshed at the same time. We can only assume that each part occasionally gets refreshed.
Our model works as follows. The adversary submits to the game a message m and the game samples \((X^0, X^1) \leftarrow \mathsf {Encode}(m)\). The adversary can then repeatedly submit leakage or tamper queries. In a leakage query the adversary submits (i, L) and is given \(R = L(X^i)\). In a tampering query the adversary submits \((T^0,T^1)\) and is given \(m' = \mathsf {Decode}(T^0(X^0), T^1(X^1))\).Footnote 1 The adversary can also make a refresh query by submitting an index j to the game. Then the game refreshes the corresponding part: \(E^j \leftarrow \mathsf {Refresh}_j(E^j)\). We give a simulation-based security definition. The simulator is not given m. To simulate a leakage query the simulator is given (j, L) and must return some value R to the adversary. To simulate a tampering query the simulator is given \((T^0, T^1)\) and must return some value \(m'\), where \(m'=*\) is replaced with \(m'=m\) before \(m'\) is returned to the adversary. To simulate a refresh query the simulator is given j and has to return nothing. The adversary must not be able to tell whether it is interacting with the real world or the simulator. The only restriction on the adversary is that the length of the leakage and the number of tampering attacks in between refreshes must be limited. For any polynomials \(p(\kappa ),q(\kappa )\) we construct a code that can tolerate \(p(\kappa )\) bits of leakage and \(q(\kappa )\) many tampering attacks in between successful refreshes.
Our definition is not strong according to the notions of Non-Malleable Codes given in the original paper [20]. In the security experiment of the strong NMCs the adversary receives either the entire tampered codeword (as opposed to receive the decoded message of the tampered codeword) or \(*\) in case that the tampering function keeps the codeword unaltered. The goal of the adversary is to distinguish the codewords of two different message given the result of the tampering function. However, such definition cannot be met in presence of a split-state refresh algorithm. In fact the adversary could forward, as tampering function, the refreshing function itself and receives a valid codeword (since it won’t be the same codeword). Given the codeword, it can easily distinguish by decoding.
Our techniques borrow ideas from both [25, 34]. In \(X^1\) we will keep a secret key sk for a public-key encryption scheme. In \(X^0\) we will keep the corresponding public key \( pk = \mathsf {PK}( sk )\), an encryption \(c=\mathsf {Enc}( pk ,m)\) of the encoded message and a simulation-sound NIZK proof of knowledge \(\pi \) of some \( sk \) such that \( pk = \mathsf {PK}( sk )\) using c as a label. Decoding will check the proof and if it is correct and \( sk \) matches \( pk \). If so, it outputs \(\mathsf {Dec}( sk ',c)\). To tolerate leakage and to allow refreshing we use a leakage resilient encryption scheme which allows to refresh \( sk \) and c independently. The public key pk in \(X^1\) will never be refreshed, which is secure as pk might in fact be public. To allow the proof of knowledge to be refreshed we use a non-malleable proof with some controlled malleability. We give a concrete instantiation of this framework based on the Continual Leakage-Resilient scheme of Dodis et al. [18] and the Controlled-Malleable NIZK system of Chase et al. [10] instantiated with Groth-Sahai proofs [30].
The structure of the encoding scheme is very similar to the one proposed by [34], however there are few substantial differences: 1. We substitute the PKE and the NIZK scheme with cryptographic primitives that allow efficient refresh mechanisms; 2. The NP relationship of the NIZK is different. (In fact, it is inspired by the scheme of [25].)
The main proof technique is to reduce tampering to legal leakage queries on the encryption scheme. In the reduction we are given separate leakage oracles of \( sk \) and c. To simulate leakage from \(X^1\), leak from \( sk \). To simulate leakage from \(X^0\), once and for all produce a simulated proof \(\pi \) with label c and simulate each leakage query from \(X^0\) by leaking from \(( pk , c, \pi )\). As for tampering queries, assume that the parts have been tampered into \(X'^1 = sk '\) and \(X'^0 = ( pk ', c', \pi ')\). First we use leakage to check whether the decoding would fail. Leak from \(X'^1\) the value \( pk ''=\mathsf {PK}(sk')\). Then leak from \(X'^0\) a single bit telling whether \( pk ' = pk ''\) and whether \(\pi '\) is a valid proof. This is exactly enough to determine whether the decoding would fail or not. If the decoding would fail, output \(\bot \). Otherwise, if the proof \(\pi '\) still has c as label (which implies that \(X'^0 = ( pk '', c, \pi ')\) when the proof is valid), then output \(*\) indicating that the decoding would output the original encoded message. If the label of \(\pi '\) is not c, then use the extraction trapdoor of the proof to extract the secret key \( sk '\) matching \( pk ''\). Then output \(\mathsf {Dec}( sk ',c')\). This allows to simulate each tampering attack with limited leakage on \(X^0\) and \(X^1\). Therefore the scheme remains secure as long as refreshing happens often enough for the leakage needed to simulate tampering to not grow about the leakage tolerance of the encryption scheme.
In [18], it was shown that Continually Leakage-Resilient Codes with Split-State Refresh are impossible to construct without computational assumptions. The result holds even when the leakage between each updates is 1 bit. It is easy to see that the same result holds for Non-Malleable Codes with Split-State Refresh. (This is because a tampering attack corresponds at least to 1 bit of leakage.)
More Related Work. Non-Malleable Codes were introduced to achieve tamper-proof security of arbitrary cryptographic primitives. Since their introduction many works have constructed NMCs in different models both under cryptographic assumptions or information theoretically (see [1,2,3, 12, 15, 19, 26, 32, 38]).
A related line of work on tamper resilience (see [14, 27, 31, 33]) aims at constructing secure compilers protecting against tampering attacks targeting the computation carried out by a cryptographic device (typically in the form of boolean and arithmetic circuits).
A third line of work on tamper resilience instead aims at constructing ad hoc solutions for different contexts like for example symmetric encryption [6, 28, 36], public-key encryption [5, 7, 16, 17, 24, 35, 39], hash functions [29] and more [8, 13, 38].
Roadmap. In the following we will first introduce some known notation and abstract definitions of the properties we need from the primitives in the abstract framework. Then we describe and prove the abstract framework, followed by an instantiation based on External Diffie-Hellman assumption [4, 9]. At the end we will present the application to continual-tamper-and-leakage resilient cryptography in more details.
2 Preliminaries
2.1 Notation and Probability Preliminaries
We let \(\mathbb {N}\) denote the naturals and \(\mathbb {R}\) denote the reals. For \(a,b \in \mathbb {R}\), we let \([a,b]=\{x\in \mathbb {R}\ :\ a\le x\le b\}\); for \(a\in \mathbb {N}\) we let \([a] = \{0,1,\ldots ,a\}\). If x is a bit-string, we denote its length by |x| and for any \(i\le |x|\) we denote with \(x_{(i)}\) the i-th bit of x; If \(\mathcal {X}\) is a set, \(|\mathcal {X}|\) represents the number of elements in \(\mathcal {X}\). When x is chosen randomly in \(\mathcal {X}\), we write  . When \(\mathsf {A}\) is an algorithm, we write \(y \leftarrow \mathsf {A}(x)\) to denote a run of \(\mathsf {A}\) on input x and output y; if \(\mathsf {A}\) is randomized, then y is a random variable and \(\mathsf {A}(x;r)\) denotes a run of \(\mathsf {A}\) on input x and randomness r. An algorithm \(\mathsf {A}\) is probabilistic polynomial-time (\(\text {PPT}\)) if \(\mathsf {A}\) is allowed to use random choices and the computation of \(\mathsf {A}(x;r)\) terminates in at most \( poly (|x|)\) steps for any input \(x\in \{0,1\}^*\) and randomness \(r \in \{0,1\}^*\).
. When \(\mathsf {A}\) is an algorithm, we write \(y \leftarrow \mathsf {A}(x)\) to denote a run of \(\mathsf {A}\) on input x and output y; if \(\mathsf {A}\) is randomized, then y is a random variable and \(\mathsf {A}(x;r)\) denotes a run of \(\mathsf {A}\) on input x and randomness r. An algorithm \(\mathsf {A}\) is probabilistic polynomial-time (\(\text {PPT}\)) if \(\mathsf {A}\) is allowed to use random choices and the computation of \(\mathsf {A}(x;r)\) terminates in at most \( poly (|x|)\) steps for any input \(x\in \{0,1\}^*\) and randomness \(r \in \{0,1\}^*\).
Let \(\kappa \) be a security parameter. A function \( negl \) is called negligible in \(\kappa \) (or simply negligible) if it vanishes faster than the inverse of any polynomial in \(\kappa \). For a relation \(\mathcal {R}\subseteq \{0,1\}^{*}\times \{0,1\}^{*}\), the language associated with \(\mathcal {R}\) is \(L_\mathcal {R}= \{x:\exists w\text { s.t. }(x,w)\in \mathcal {R}\}\).
For two ensembles \(\mathcal {X}=\{X_\kappa \}_{\kappa \in \mathbb N}\), \(\mathcal {Y}=\{Y_\kappa \}_{\kappa \in \mathbb N}\), we write \(\mathcal X \mathop {\mathop {\approx }\limits ^{c}}\nolimits _\epsilon \mathcal Y\), meaning that every probabilistic polynomial-time distinguisher D has \(\epsilon (\kappa )\) advantage in distinguishing \(\mathcal X\) and \(\mathcal Y\), i.e., \(\frac{1}{2} \vert \mathbb {P}[D(\mathcal X_\kappa )=1] - \mathbb {P}[D(\mathcal Y_\kappa )=1] \vert \le \epsilon (\kappa )\) for all sufficiently large values of \(\kappa \).
We simply write \(\mathcal X {\mathop {\approx }\limits ^{c}} \mathcal Y\) when there exists a negligible function \(\epsilon \) such that \(\mathcal {X} \mathop {\mathop {\approx }\limits ^{c}}\nolimits _\epsilon \mathcal {Y} \). Similarly, we write \(\mathcal X \approx _\epsilon \mathcal Y\) (statistical indistinguishability), meaning that every unbounded distinguisher has \(\epsilon (\kappa )\) advantage in distinguishing \(\mathcal {X} \) and \(\mathcal {Y} \).
Given a string \(X=(X^1,X^2)\in (\{0,1\}^*)^2\) and a value \(\ell \in \mathbb {N}\) let \(\mathcal {O} _\ell (X)\) be the split-state leakage oracle. \(\mathcal {O} _\ell (X)\) accepts as input tuple of the form (i, f) where the first element i is an index in \(\{0,1\}\) and the the second element f is a function defined as a circuit. If the total amount of leakage is below \(\ell \), \(\mathcal {O} _\ell (X)\) outputs \(f_1(X^{i_1})\) otherwise it outputs the special symbol \(\bot \). More formally, the oracle \(\mathcal {O} _\ell (X)\) is a state machine that maintains state variables \(\mathcal {O} _\ell (X).l^0\) and \(\mathcal {O}_\ell (X).l_1\) and upon input (i, f) where f is an efficiently computable function with co-domain \(\{0,1\}^{o}\) for a value \(o\in \mathbb {N}\) outputs \(f(X^{i})\) if \((l^i+o) \le \ell \) and then updates the value \(l^i\) to \(l^i+o\), otherwise it outputs the value \(\bot \).
Given two \(\text {PPT}\) interactive algorithms \(\mathsf {A}\) and \(\mathsf {B}\) we write \((y,k)\leftarrow \mathsf {A}(x)\leftrightarrows \mathsf {B}(z)\) to denote the joint execution of the algorithm \(\mathsf {A}\) with input x and the algorithm \(\mathsf {B}\) with input z. The string y (resp. z) is the output of \(\mathsf {A}\) (resp. \(\mathsf {B}\)) after the interaction. In particular we write \(\mathsf {A}\leftrightarrows \mathcal {O} _{\ell }(X)\) to denote \(\mathsf {A}\) having oracle access to the leakage oracle with input X. Moreover, we write \(\mathsf {A}\leftrightarrows \mathcal {B},\mathcal {C} \) to denote \(\mathsf {A}\) interacting in an interleaved fashion both with \(\mathcal {B} \) and with \(\mathcal {C} \).
2.2 Cryptographic Primitives
NIZK Proof of Knowledge. We first introduce the necessary notation for label-malleable NIZK (lM-NIZK for short) argument system. A label-malleable NIZK is intuitively a non-malleable NIZK except that from a proof under a given label one can generate a new proof for the same statement under a different label without using the witness. A lM-NIZK \(\mathcal {NIZK}:=(\mathsf {I},\mathsf {P},\mathsf {V},\mathsf {RandProof},\mathsf {LEval})\) with label space \(\mathcal L\) is a tuple of \(\text {PPT}\) algorithms where: (1) The algorithm \(\mathsf {I}\) upon input the security parameter \(1^\kappa \), creates a common reference string (CRS) \(\omega \); (2) The prover algorithm \(\mathsf {P}\) upon input \(\omega \), a label \(L\in \mathcal L\) and a valid instance x together with a witness w produces a proof \(\pi \). We write \(\mathsf {P}^L(\omega ,x,w)\); (3) The verifier algorithm \(\mathsf {V}\) upon input \(\omega \), a label L an instance x together with a proof \(\pi \) outputs a verdict in \(\{0,1\}\). We write \(\mathsf {V}^L(\omega ,x,\pi )\); (4) The label-derivation algorithm \(\mathsf {LEval}\) upon input \(\omega \), a transformation \(\phi \), a label L an instance x and a proof \(\pi \) outputs a new proof \(\pi '\).
Definition 1
(Adaptive multi-theorem zero-knowledge). Let \(\mathcal {NIZK}\) be a non-interactive argument system for a relation \(\mathcal {R}\). We say that \(\mathcal {NIZK}\) satisfies adaptive multi-theorem zero-knowledge if the following holds:
-
(i)
There exists a \(\text {PPT}\) algorithm \(\mathsf {S}_0\) that outputs a CRS \(\omega \) and a trapdoor \(\tau _{ sim }\).
-
(ii)
There exist a \(\text {PPT}\) simulator \(\mathsf {S}_1\) and a negligible function \(\nu \) such that, for all \(\text {PPT}\) adversaries \(\mathsf {A}\), we have that
$$\begin{aligned} \Big |\mathbb {P}&\left[ \mathsf {A}(\omega )\leftrightarrows {\mathsf {P}(\omega ,\cdot )}=1|~\omega \leftarrow \mathsf {I}(1^\kappa )\right] \\&- {\mathbb {P}\left[ \mathsf {A}(\omega )\leftrightarrows {\mathcal {SIM}(\tau _{ sim },\cdot )}=1|~(\omega ,\tau _{ sim })\leftarrow \mathsf {S}_0(1^\kappa )\right] }\Big |\le \nu (\kappa ). \end{aligned}$$The simulation oracle \(\mathcal {SIM}(\tau _{ sim },\cdot )\) takes as input a tuple (L, x, w) and checks if \((x,w)\in \mathcal {R}\), and, if true, ignores w and outputs a simulated argument \(\mathsf {S}_1(\tau _{ sim },L,x)\), and otherwise outputs \(\bot \).
Given \(\mathcal {NIZK}\) that supports the set of labels \(\mathcal L\), we say that a set \(\mathcal {T}\) is a set of label transformations for \(\mathcal {NIZK}\) iff for any \(\phi \in \mathcal {T}\) the co-domain of \(\phi \) is a subset of \(\mathcal L\).
Definition 2
( \(\mathcal {T} \) -Malleable Label Simulation Extractability). Let \(\mathcal {T} \) be a set of label transformations for \(\mathcal {NIZK}\). Let \(\mathcal {NIZK}\) be a non-interactive argument system for a relation \(\mathcal {R}\). We say that \(\mathcal {NIZK}\) is \(\mathcal {T} \) -malleable label simulation extractable (\(\mathcal {T} \)-ml-SE) if the following holds:
-
(i)
There exists an algorithm \(\mathsf {S}_0\) that outputs a CRS \(\omega \), a simulation trapdoor \(\tau _{ sim }\), and an extraction trapdoor \(\tau _{ ext }\).
-
(ii)
There exists a \(\text {PPT}\) algorithm \(\mathsf {Ext}\) such that, for all \(\text {PPT}\) adversaries \(\mathsf {A}\), the probability, taken over the experiment \(\mathbf {Exp}^{\mathcal {T}-\mathsf {lmSE}}_{\mathsf {Ext},\mathsf {S},\mathsf {A}}\) (as defined in Fig. 1), of the conjunction of the following events is negligible in the security parameter \(\kappa \):
-
(a)
\((L^*,x^*)\not \in \mathcal {Q} \) and \(\mathsf {V}(\omega ,L^*,x^*,\pi ^*) = 1\);
-
(b)
\((x^*,w)\not \in \mathcal {R}\);
-
(c)
Either \(\phi \not \in \mathcal {T} \) or for any (L, x) either \((L,x)\not \in \mathcal {Q} \) or \(\phi (L)\ne L^*\).
Moreover, we say that \(\mathsf {A}\) wins the \(\mathcal {T} \)-lm SE Experiment when all the above events happen.
-
(a)
Definition 3
(Label Derivation Privacy). Let \(\mathcal {NIZK}\) a lM-NIZK, and let \(\mathcal {T} \) be a set of label transformations. We say that \(\mathcal {NIZK}\) has label derivation privacy if for all \(\text {PPT}\) \(\mathsf {A}\), there exists a negligible function \( negl \) such that \((\mathsf {P}\left[ \mathbf {Exp}^{\mathcal {T}-\mathsf {lDP}}_{\mathcal {NIZK}}(\kappa )=1\right] - \tfrac{1}{2}) \le negl (\kappa ) \) (where the experiment is defined in Fig. 1).
Public-Key Encryption. A public-key encryption (PKE) scheme is a tuple of algorithms \(E= (\mathsf {Setup},\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) defined as follows. (1) Algorithm \(\mathsf {Setup}\) takes as input the security parameter and outputs public parameters \({ pub }\in \{0,1\}^*\). all algorithms are implicitly given \({ pub }\) as input. (2) Algorithm \(\mathsf {Gen}\) takes as input the security parameter and outputs a public/secret key pair \(( pk , sk )\); the set of all secret keys is denoted by \(\mathcal {SK}\) and the set of all public keys by \(\mathcal {PK}\). Additionally, we require the existence of a \(\text {PPT}\) function \(\mathsf {PK}\) which upon an input \( sk \in \mathcal {SK}\) produces a valid public key \( pk \). (3) The randomized algorithm \(\mathsf {Enc}\) takes as input the public key \( pk \), a message \(m\in \mathcal {M}\), and randomness \(r\in \mathcal {R}\), and outputs a ciphertext \(c = \mathsf {Enc}( pk ,m;r)\); the set of all ciphertexts is denoted by \(\mathcal {C}\). (4) The deterministic algorithm \(\mathsf {Dec}\) takes as input the secret key \( sk \) and a ciphertext c, and outputs \(m = \mathsf {Dec}( sk ,c)\) which is either equal to some message \(m\in \mathcal {M}\) or to an error symbol \(\bot \). Additionally, we also consider two \(\text {PPT}\) algorithms: 1. Algorithm \(\mathsf {UpdateC}\) takes as input a public key \( pk \) a ciphertext c and outputs a new ciphertext c. 2. Algorithm \(\mathsf {UpdateS}\) takes as input a secret key \( sk \) and outputs a new secret key \( sk '\).
Correctness (with Updates). We say that \(E\) satisfies correctness if for all \({ pub }\leftarrow \mathsf {Setup}(1^\kappa )\) and \(( pk , sk )\leftarrow \mathsf {Gen}({ pub })\) we have that:
where the randomness is taken over the internal coin tosses of algorithms \(\mathsf {Enc}\), \(\mathsf {UpdateS}\) and \(\mathsf {UpdateC}\). Additionally, we require that for any \( pk , sk \leftarrow \mathsf {Gen}({ pub })\): (A) any \( sk '\) such that \(\mathsf {PK}( sk ')= pk \) and any \(c\in \mathcal {C} \) we have that \(\mathsf {Dec}( sk ,c)=\mathsf {Dec}( sk ',c)\); (B) any \( sk '\leftarrow \mathsf {UpdateS}( sk )\) we have that \(\mathsf {PK}( sk )=\mathsf {PK}( sk ')\).
CLRS Friendly PKE Security. We now turn to define Continual-Leakage Resilient Storage Friendly public key encryption.
Definition 4
For \(\kappa \in \mathbb {N}\), let \(\ell = \ell (\kappa )\) be the leakage parameter. We say that \(E= (\mathsf {Setup},\mathsf {Gen},\mathsf {Enc},\mathsf {Dec},\mathsf {UpdateC},\mathsf {UpdateS})\) is \(\ell \)-CLRS Friendly if for all \(\text {PPT}\) adversaries \(\mathsf {A}\) there exists a negligible function \(\nu :\mathbb {N}\rightarrow [0,1]\) such that \( \left| {\mathbb {P}\left[ \mathbf {Exp}^{\mathrm {clrs}}_{E,\mathsf {A}}(\kappa ,\ell ) = 1\right] } - \frac{1}{2}\right| \le \nu (\kappa ), \) (where the experiment is defined in Fig. 2).
We observe that Definition 4 is weaker than the definition of Dodis et al. [18], in fact we do not consider leakage from the update process. We introduce an extra property on the \(\mathsf {UpdateC}\) algorithm of a CLRS Friendly PKE.
Definition 5
We say that \(E\) is perfectly ciphertext-update private if for any \(\kappa \in \mathbb {N}\), \({ pub }\leftarrow \mathsf {Setup}(1^\kappa )\), \(( pk , sk )\leftarrow \mathsf {Gen}({ pub })\) and any \(m\in \mathcal {M}\) the distributions \(\{\mathsf {Encode}( pk ,m)\}\) and \(\{\mathsf {UpdateC}( pk ,\mathsf {Enc}( pk ,m))\}\) are equivalent.
If \(E\) is a CLRS Friendly PKE then the weaker version of the property above where the two distributions are computationally indistinguishable already holds. The construction in Sect. 4 can be proved secure using the computational ciphertext-update privacy property. However, we prefer to include the perfectly ciphertext-update privacy property because it simplifies the exposition.
3 Definition
In this section we consider three definitions of Non-Malleable Codes with Refresh (NMC-R). The syntax given allows the scheme to depends on a common reference string following [34].
A coding scheme in the CRS model is a tuple \(\varSigma =(\mathsf {Init},\mathsf {Encode},\mathsf {Decode})\) of \(\text {PPT} \) algorithms with the following syntax: (1) \(\mathsf {Init}\) on input \(1^\kappa \) outputs a common reference string \( crs \). (2) \(\mathsf {Encode}\) on inputs \( crs \) and a message \(m\in \mathcal {M} _\kappa \) outputs \(X \in \mathcal {C} _\kappa \); (3) \(\mathsf {Decode}\) is a deterministic algorithm that on inputs \( crs \) and a codeword \(X \in \mathcal {C} _\kappa \) decodes to \(m'\in \mathcal {M} _\kappa \). A coding scheme is correct if for any \(\kappa \) and any \(m\in \mathcal {M} _\kappa \) we have \(\mathbb {P}_{ crs ,r_e}[\mathsf {Decode}( crs ,\mathsf {Encode}( crs ,m;r_e))=m]=1\).
We consider coding schemes with an efficient refreshing algorithm. Specifically, for a coding scheme \(\varSigma \) there exists an algorithm \(\mathsf {Rfrsh}\) that upon inputs \( crs \) and a codeword \(X\in \mathcal {C} _\kappa \) outputs a codeword \(X\in \mathcal {C} _\kappa \). For correctness we require that \({\mathbb {P}\left[ \mathsf {Decode}( crs ,\mathsf {Rfrsh}( crs ,X))=\mathsf {Decode}( crs ,X)\right] }=1\), where the probability is over the randomness used by the algorithms and the generation of the CRS.
We are interested in coding schemes in the split-state model where the two parts can be refreshed independently and without the need of any interactions. Given a codeword \(X:=(X^0,X^1)\), we consider the procedure \(\mathsf {Rfrsh}( crs ,\ (i,X^i))\) for \(i\in \{0,1\}\) that takes the i-th piece of the codeword and outputs a new piece \(X'^i\). Abusing of notation, given a codeword \(X:=(X^0,X^1)\) when we write \(\mathsf {Rfrsh}( crs , X)\) we implicitly mean the execution of both \(\mathsf {Rfrsh}( crs , (i,X^0))\) and \(\mathsf {Rfrsh}( crs , (i,X^1))\). Similarly, given a split-state function \(T=(T^0,T^1)\) we equivalently write T(X) meaning the application of both \(T^0(X^0)\) and \(T^1(X^1)\).
We require that for any codeword \(X:=(X^0,X^1)\) and for any \(i\in \{0,1\}\), let \(\bar{X}\) such that \(\bar{X}^i\leftarrow \mathsf {Rfrsh}( crs , (i,X^i))\) and \(\bar{X}^{i-1}= X^{i}\) then \(\mathbb {P}[\mathsf {Decode}( crs ,\bar{X})=\mathsf {Decode}( crs ,X)]=1\).
NMC with Refresh in the STM. We now give the security definition for Non-Malleable Codes with Refresh. Although the definition would be meaningful for a more general setting, for the sake of concreteness, we specialize it for the split-state model. Let \(I_m\) be a function from \(\mathcal {M}\cup \{*\}\) to \(\mathcal {M}\) which substitutes the symbol \(*\) in input with the message m and acts as the identity function otherwise. Let \(\mathbf {Tamper}\) and \(\mathbf {SimTamper}\) be the experiments described in Fig. 3.
Definition 6
(Non-Malleable Codes with Refresh). For \(\kappa \in \mathbb {N}\), let \(\ell =\ell (\kappa ),\rho =\rho (\kappa ),\tau =\tau (\kappa )\) be parameters. We say that the coding scheme \(\varSigma \) is a \((\ell ,\rho ,\tau )\)-Non-Malleable Code with Refresh (NMC-R) in the split state model if for any adversary \(\mathsf {A}=(\mathsf {A}_0,\mathsf {A}_1,\mathsf {A}_2)\) where \(\mathsf {A}_0\) and \(\mathsf {A}_2\) are a \(\text {PPT}\) algorithm and \(\mathsf {A}_1\) is deterministic polynomial time, there exists a \(\text {PPT}\) simulator \(\mathsf {S}=(\mathsf {S}_0,\mathsf {S}_1,\mathsf {S}_2,\mathsf {S}_3)\) and a negligible function \(\nu \) such that
We give some remarks regarding the definition above. The simulator \(\mathsf {S}\) is composed of four different parts \(\mathsf {S}_0,\mathsf {S}_1,\mathsf {S}_2,\mathsf {S}_3\). The algorithm \(\mathsf {S}_0\) upon input \(1^\kappa \) produces a CRS together with some trapdoor information \( aux \), the CRS produced and the output of \(\mathsf {Init}\) are computational indistinguishable.
For simplicity, we assume that the state information \( aux \) is stored in a common read-and-write memory that the simulators \(\mathsf {S}_0,\mathsf {S}_1,\mathsf {S}_2,\mathsf {S}_3\) have access to. We will sometime referee to \(\mathsf {S}_1\) as the tampering simulator, to \(\mathsf {S}_2\) as the leakage simulator and to \(\mathsf {S}_3\) as the refresh simulator.
The adversary \(\mathsf {A}\) is composed by a \(\text {PPT}\) algorithm \(\mathsf {A}_0\), a deterministic algorithm \(\mathsf {A}_1\) and \(\text {PPT}\) distinguishing algorithm \(\mathsf {A}_2\). The adversary \(\mathsf {A}_0\) can sample a message m (as function of the CRS) and some state information z. The latter may encode some side information z about the message m and other information that \(\mathsf {A}_0\) wants to pass to \(\mathsf {A}_1\). Notice that we can assume without loss of any generality \(\mathsf {A}_1\) to be deterministic, in fact, z may also contain random coins. The tampering simulator, the leakage simulator and the refresh simulator take as input the state information z. In addition, in each round, the tampering simulator \(\mathsf {S}_1\) receives a split-state tampering function \(T_{i+1}\) and it outputs a message \(\bar{m}_{i+1}\). First, we notice that, in general, the tampering \(T_{i+1}\) can be produced as a function of the initial message m, therefore the simulator (which does not know m) cannot compute the tampering function by its own, even given z. Secondly, the adversary can efficiently produce a tampering function that keeps the same encoded message but modifies the codeword (for example, by submitting the refreshing algorithm \(\mathsf {Rfrsh}\) as tampering function). The task of the tampering simulator is to detect this (outputting the special symbol \(*\)), in this case the function \(I_{m}\) forwards to \(\mathsf {A}\) the initial message m. (We stress that the simulator does not know the message m, so it cannot forward m directly to \(\mathsf {A}\) but it needs to pass by \(I_{m}\).)
The tamper experiment takes four parameters: the security parameter \(\kappa \), the leakage parameter \(\ell \), the round parameter \(\rho \) and the tampering parameter \(\tau \). The tampering parameter \(\tau \) counts how many times the adversary can tamper with the codeword before a refresh of the codeword is needed.
4 Construction
Let \(E=(\mathsf {Setup},\mathsf {Gen},\mathsf {Enc},\mathsf {Dec},\mathsf {UpdateC},\mathsf {UpdateS})\) be a CLRS friendly PKE with ciphertext space \(\mathcal {C} _E\). Let \(\mathcal {R}\) be the \( NP \) relation defined below:
Let \(\mathcal {T} \) be a set of label transformations defined below:
Notice that both \(\mathcal {R}\) and \(\mathcal {T}\) are implicitly parametrized by the public parameters \({ pub }\) of the PKE scheme. Let \(\mathcal {U} \) be the following set of label transformations:
It is easy to check that \(\mathcal {U} \subseteq \mathcal {T} \). In fact, by the correctness of PKE, there exists \( sk \) such that \({\mathbb {P}\left[ \mathsf {Dec}( sk ,\mathsf {UpdateC}( pk ,\mathsf {Enc}( pk ,m))=m\right] }=1\) and \( pk =\mathsf {PK}( sk )\).
Let \(\mathcal {NIZK}:=(\mathsf {I},\mathsf {P},\mathsf {V},\mathsf {LEval})\) be a lM-NIZK argument system for the relation \(\mathcal {R}\) with label space \(\mathcal {C}_E\) and set of transformation \(\mathcal {T}\). Let \(\varSigma \) be the following coding scheme with refresh in the CRS model:
-
 Sample \(\omega \leftarrow \mathsf {I}(1^\kappa )\) and \({ pub }\leftarrow \mathsf {Setup}(1^\kappa )\). Return \( crs =(\omega ,{ pub })\).
Sample \(\omega \leftarrow \mathsf {I}(1^\kappa )\) and \({ pub }\leftarrow \mathsf {Setup}(1^\kappa )\). Return \( crs =(\omega ,{ pub })\). -
 Parse \( crs =(\omega ,{ pub })\), sample \(( sk , pk )\leftarrow \mathsf {Gen}({ pub })\), compute \(c \leftarrow \mathsf {Enc}( pk ,m)\) and \(\pi \leftarrow \mathsf {P}^{c}(\omega , pk , sk )\). Set \(X^0:=( pk ,c,\pi )\) and \(X^1:= sk \) and return \(X:=(X^0,X^1)\).
Parse \( crs =(\omega ,{ pub })\), sample \(( sk , pk )\leftarrow \mathsf {Gen}({ pub })\), compute \(c \leftarrow \mathsf {Enc}( pk ,m)\) and \(\pi \leftarrow \mathsf {P}^{c}(\omega , pk , sk )\). Set \(X^0:=( pk ,c,\pi )\) and \(X^1:= sk \) and return \(X:=(X^0,X^1)\). -
 Parse \( crs =(\omega ,{ pub })\) and \(X=(X^0,X^1)\) where \(X^1= sk \) and \(X^0=( pk ,c,\pi )\). Check: (A) \( pk =\mathsf {PK}( sk )\) and (B) \(\mathsf {V}^{c}(\omega , pk ,\pi )=1\).
Parse \( crs =(\omega ,{ pub })\) and \(X=(X^0,X^1)\) where \(X^1= sk \) and \(X^0=( pk ,c,\pi )\). Check: (A) \( pk =\mathsf {PK}( sk )\) and (B) \(\mathsf {V}^{c}(\omega , pk ,\pi )=1\).If both checks (A) and (B) hold then return \(\mathsf {Dec}( sk ,c)\), otherwise return \(\bot \).
-

-
–
\(j=0\), parse \(X^0=(c, pk ,\pi )\),
 , compute \(c':= \mathsf {UpdateC}( pk ,c;r)\) and \(\pi '\leftarrow \mathsf {LEval}\left( \omega ,\ \mathsf {UpdateC}( pk ,\cdot ;r),\ ( pk ,c,\pi ) \right) \), return \(X^0:=( pk ,c',\pi ')\).
, compute \(c':= \mathsf {UpdateC}( pk ,c;r)\) and \(\pi '\leftarrow \mathsf {LEval}\left( \omega ,\ \mathsf {UpdateC}( pk ,\cdot ;r),\ ( pk ,c,\pi ) \right) \), return \(X^0:=( pk ,c',\pi ')\). -
–
\(j=1\), parse \(X^1= sk \) and compute \( sk '\leftarrow \mathsf {UpdateS}( sk )\), return \(X^1:=( sk ')\).
-
–
Theorem 1
For any polynomial \(\tau (\kappa )\), if \(E\) is an \(\ell '\)-CLRS-Friendly PKE scheme (Definition 4) with public key space \(\mathcal {PK}\) and message space \(\mathcal {M} \) and where \(\ell '(\kappa ):=\ell (\kappa )+\tau (\kappa )\cdot (\max (\kappa +1,\log (|\mathcal {M} |+2)+1,\log |\mathcal {PK}|))\) and if \(\mathcal {NIZK}\) is an adaptive multi-theorem zero-knowledge (Definition 1) label-malleable non-interactive argument of knowledge system with malleable label simulation extractability (Definition 2) and label derivation privacy (Definition 3) then the scheme above is a \((\ell ,\rho , \tau )\)-Non-Malleable Code with Refresh for any polynomial \(\rho (\kappa )\).
The leakage rate of the encoding scheme depends on the relation between the size of the proofs of the NIZK system and the parameters of the CLRS Friendly PKE. Roughly, setting \(\tau \) be a constant, assuming the size of the secret key and the size of the ciphertext of the PKE be approximately the same and let \(r=| sk |/\ell \) be the leakage ratio of the CLRS-Friendly PKE then the leakage ratio of the coding scheme is strictly less than \(r/(2+1/ poly (\kappa ))\). This comes from the extractability propertyFootnote 2 of the NIZK system and the \(O(\kappa )\)-bits of leakage needed to support tampering attacks.
Proof
The correctness follows immediately from the correctness of the \(E\) and \(\mathcal {NIZK}\) and \(\mathcal {U} \subseteq \mathcal {T} \). The proof of security is divided in two parts. We first define a simulator, then we define a sequence of mental experiments starting with the initial \(\mathbf {Tamper}\) experiment and proceeding toward the \(\mathbf {SimTamper}\) experiment and we prove that the experiments are computationally indistinguishable.
The Simulator. Let \(\widetilde{\mathsf {S}}\) be the simulator of the \(\mathcal {NIZK}\) as postulated by Definition 1. Given an adversary \(\mathsf {A}=(\mathsf {A}_0,\mathsf {A}_1,\mathsf {A}_2)\) consider the following simulator \(\mathsf {S}=(\mathsf {S}_0,\mathsf {S}_1,\mathsf {S}_2,\mathsf {S}_3)\) for the \(\mathbf {SimTamper}\) experiment:

-
Set the variables \(t^0,t^1,l^0,l^1\) to 0.
-
Run the \(\mathcal {NIZK}\) simulator \((\omega ,\tau _{ sim },\tau _{ ext })\leftarrow \widetilde{\mathsf {S}}_0(1^\kappa )\).
-
Sample \(( pk , sk )\leftarrow \mathsf {Gen}({ pub })\), \(c \leftarrow \mathsf {Enc}( pk ,0^\kappa )\) and \(\pi \leftarrow \tilde{\mathsf {S}}_1(\omega ,c, pk )\).
-
Set the joint state \( aux \) to \((\tau _{ sim },\tau _{ ext },X^0,X^1,t^0,t^1)\) where \((X^0,X^1)=(( pk ,c,\pi ),( sk ))\).

-
Parse \(T=(T^0,T^1)\) and \( aux \) as \((\tau _{ sim },\tau _{ ext },X^0,X^1,t^0,t^1)\) where \((X^0,X^1)=(( pk ,c,\pi ),( sk ))\).
-
Compute \(\tilde{X}^i=T^i(X^i)\) for \(i\in \{0,1\}\).
-
Check \(\tilde{ pk }=\mathsf {PK}(\tilde{ sk })\) and \(\mathsf {V}^{\tilde{c}}(\omega ,\tilde{ pk },\tilde{\pi })=1\) (check (A) and (B) of \(\mathsf {Decode}\)), if at least one of the checks fails then return \(\bot \).
-
Compute \(( sk ',\phi ,c')\leftarrow \mathsf {Ext}(\tau _{ ext },\tilde{c},\ \tilde{ pk },\tilde{\pi })\):
-
(I)
If \(\tilde{ pk }=\mathsf {PK}( sk ')\) then output \(\tilde{m}= \mathsf {Dec}( sk ',\tilde{c})\);
-
(II)
If \(\phi (c')= \tilde{c}\), \(c'=c\) and \(T\in \mathcal {T} \) return \(*\);
-
(III)
Else abort.
-
(I)

-
Parse \( aux \) as \((\tau _{ sim },\tau _{ ext },X^0,X^1,t^0,t^1,l^0,l^1)\) where \((X^0,X^1)=(( pk ,c,\pi ),( sk ))\).
-
Upon message (i, L) where \(i\in \{0,1\}\), compute \(y\leftarrow L(X^i)\). If \(l^i+|y| \le \lambda \) then update \(l^i:=l^i+|y|\) and output y else output \(\bot \).

-
Parse \( aux \) as \((\tau _{ sim },\tau _{ ext },X^0,X^1,t^0,t^1,l^0,l^1)\) where \((X^0,X^1)=(( pk ,c,\pi ),( sk ))\); If \(j\not \in \{0,1\}\) and \(t^{0},t^{1}\le \tau \) set \(X_{i+1}:=X_{i}\); Else:
-
– If \(j=0\) or \((t^{0}> \tau )\) then compute \(c'\leftarrow \mathsf {UpdateC}( pk ,c)\) and \(\pi '\leftarrow \widetilde{\mathsf {S}}_1(\tau _{ sim }, c', pk )\) and reset \(l^0,t^0\) to 0;
-
– If \(j=1\) or \((t^{1}> \tau )\) then compute \( sk '\leftarrow \mathsf {UpdateS}( sk )\) and reset \(l^1,t^1\) to 0.
-
-
Set \( aux \) as \((\tau _{ sim },\tau _{ ext },X'^0,X'^1,t^0,t^1,l^0,l^1)\) where \((X'^0,X'^1)=(( pk ,c',\pi '),( sk '))\).
The Hybrids. We consider a sequence of mental experiments, starting with the initial \(\mathbf {Tamper}\) experiment which for simplicity we denote by \(\mathbf {G}_0\). We summarize the sequence of mental experiments in Fig. 4.
Games in the proof of Theorem 1. Game \(\mathbf {G}_0\) does not execute any of the colored actions, whereas each colored game executes all actions from the previous game plus the ones of the corresponding color. \(\mathbf {G}_6\) executes all actions from the previous game but it does not execute the dash-boxed instructions. Additionally, \(\mathbf {G}_8\) does not execute any of the boxed instructions.
-
Game \(\mathbf {G}_0\). This is exactly the game defined by the experiment \(\mathbf {Tamper}\), where \(\varSigma \) is the coding scheme described above. In particular, the \(\mathsf {Init}\) algorithm of \(\varSigma \) samples a CRS \(\omega \leftarrow \mathsf {I}(1^\kappa )\) for \(\mathcal {NIZK}\), a pair \(( pk , sk _0)\leftarrow \mathsf {Gen}({ pub })\), encrypts \(c_0\leftarrow \mathsf {Enc}( pk ,m)\) and computes \(\pi _0\leftarrow \mathsf {P}^c(\omega , pk , sk )\). The \(\mathsf {Rfrsh}^*\) algorithm if \(\varSigma \) upon input \(j=0\) samples randomness
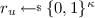 , defines the transformation \(\phi _u(\cdot ):=\mathsf {UpdateC}( pk ,\cdot \ ;r_u)\) and computes \(c_{i+i}:=\phi _u(c_i)\) and \(\pi _{i+1}:=\mathsf {LEval}(\omega ,\phi _u,\ ( pk ,c_i,\pi _i))\).
, defines the transformation \(\phi _u(\cdot ):=\mathsf {UpdateC}( pk ,\cdot \ ;r_u)\) and computes \(c_{i+i}:=\phi _u(c_i)\) and \(\pi _{i+1}:=\mathsf {LEval}(\omega ,\phi _u,\ ( pk ,c_i,\pi _i))\). -
Game \(\mathbf {G}_1\). We change the way the proofs \(\pi _{i+1}\) are refreshed. For each iteration \(i\in [\rho (\kappa )]\), the refresh procedure \(\mathsf {Rfrsh}^*\) upon input \(j=0\) parses \(X^0_i\) as \(( pk ,c_i,\pi _i)\), samples randomness
 , defines the transformation \(\phi _u(\cdot ):=\mathsf {UpdateC}( pk ,\cdot \ ;r_u)\), computes \(c_{i+1}\leftarrow \phi _u(c_i)\) and a fresh proof: $$\begin{aligned} \pi _{i+1}\leftarrow \mathsf {P}^{c_{i+1}}(\omega , pk , sk _i). \end{aligned}$$
, defines the transformation \(\phi _u(\cdot ):=\mathsf {UpdateC}( pk ,\cdot \ ;r_u)\), computes \(c_{i+1}\leftarrow \phi _u(c_i)\) and a fresh proof: $$\begin{aligned} \pi _{i+1}\leftarrow \mathsf {P}^{c_{i+1}}(\omega , pk , sk _i). \end{aligned}$$Finally, it sets \(X^0_{i+1}:=( pk ,c_{i+1},\pi _{i+1})\).
-
Game \(\mathbf {G}_2\). We change the way the CRS for the \(\mathcal {NIZK}\) and the proofs \(\pi _i\) are computed. Let \(\omega ,\tau _{ sim },\tau _{ ext }\leftarrow \widetilde{\mathsf {S}}_0(1^\kappa )\) and for \(i\in [\rho (\kappa )]\) if \(\mathsf {Rfrsh}^*\) is called at the i-th iteration with input \(j=0\) then the proof \(\pi _{i+1}\) is computed as:
$$\begin{aligned} \pi _{i+1}\leftarrow \widetilde{\mathsf {S}}_1(\tau _{ sim },c_{i+1}, pk ). \end{aligned}$$Also the proof \(\pi _0\) is computed in the same way.
-
Game \(\mathbf {G}_3\). We extract the witness from the proof \(\tilde{\pi }\) and abort if the extraction procedure fails. The game is the same as \(\mathbf {G}_2\) but, for each iteration i, let \(\tilde{X}_{i+1}\) be the tampered codeword where \(\tilde{X}_{i+1} = (\tilde{ pk },\tilde{c}, \tilde{\pi }),(\tilde{ sk })\). The game first checks if \(\mathsf {V}^{\tilde{c}}(\omega ,\tilde{ pk },\tilde{\pi })=1\) and if so then it runs:
$$\begin{aligned} sk ',\phi ,c'\leftarrow \mathsf {Ext}(\tau _{ ext },\tilde{\pi }). \end{aligned}$$Let C be the set of ciphertexts produced by the game until the i-th iteration. Namely \(C:=\{{c}_{0},\ldots ,{c}_{i}\}\). If both the conditions: (i) \(\tilde{ pk }=\mathsf {PK}( sk ')\) and (ii) \(\phi (c')= \tilde{c}\), \(c'\in C\) and \(\phi \in \mathcal {T} \) do not hold then the game outputs a special symbol \(\mathbf {Abort}\).
-
Game \(\mathbf {G}_4\). We change the output of \(\mathsf {Decode}\) to match point (I) of the simulator \(\mathsf {S}_1\). The game is the same as \(\mathbf {G}_3\) but, for each iteration \(i\in [\rho (\kappa )]\), after the extraction, if the condition \(\tilde{ pk }=\mathsf {PK}( sk ')\) holds, it sets the message \(m_{i+1}:=I_m(\mathsf {Dec}( sk ',\tilde{c}))\).
-
Game \(\mathbf {G}_5\). We change the output of \(\mathsf {Decode}\). The game is the same as \(\mathbf {G}_4\) but, for each iteration \(i\in [\rho (\kappa )]\), after the i-th extraction, if the conditions \(\phi (c')= \tilde{c}\), \(c'\in C\), where \(C=\{{c}_{0},\ldots ,{c}_{i}\}\) and \(\phi \in \mathcal {T} \) hold, it sets the message \(m_{i+1}:=I_m(*)\) (the original message).
-
Game \(\mathbf {G}_6\). We do not decode explicitly anymore. The game is the same as \(\mathbf {G}_5\) but, for each iteration \(i\in [\rho (\kappa )]\), in the execution of the decoding algorithm \(\mathsf {Decode}\), we do not execute the instruction \(m_{i+1}:=\mathsf {Dec}(\tilde{ sk },\tilde{c})\).
-
Game \(\mathbf {G}_7\). We change the output of \(\mathsf {Decode}\) to match point (II) of the simulator \(\mathsf {S}_1\). The game is the same as \(\mathbf {G}_6\) but, for each iteration \(i\in [\rho (\kappa )]\), after the i-th extraction, let the set C be redefined as the singleton containing the ciphertext produced after the last refresh, namely \(C:=\{c_i\}\), the game checks that the conditions \(\phi (c')= \tilde{c}\), \(c'\in C\) (instead of \(c'\in \{{c}_{0},\ldots ,{c}_{i}\}\)) and \(\phi \in \mathcal {T} \) hold then it sets the message \(m_{i+1}:=I_m(*)\) (the original message).
-
Game \(\mathbf {G}_8\). We replace the ciphertext c with a dummy ciphertext. The game is the same as \(\mathbf {G}_7\) but it sets \(c\leftarrow \mathsf {Enc}( pk ,0^\kappa )\) (instead of \(c\leftarrow \mathsf {Enc}( pk ,m)\)).
It is easy to check that \(\mathbf {G}_8\) is equivalent to the \(\mathbf {SimTamper}_{\mathsf {A},\mathsf {S}}\).
Lemma 1
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _{0,1}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_0(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_1(\kappa ) = 1\right] }\right|\le \nu _{0,1}(\kappa )\).
Proof
We reduce to label derivation privacy of \(\mathcal {NIZK}\) via an hybrid argument. For any \(l\in [\rho (\kappa )+1]\), let \(\mathbf {Hyb}_l\) be the hybrid experiment that executes the same code of \(\mathbf {G}_1\) until the l-th iteration (the proofs are new) and then executes the same code of \(\mathbf {G}_1\) (the proofs are re-labeled). In particular, for any l, in the hybrid \(\mathbf {Hyb}_l\), for any \(0\le i<l\) the proof \(\pi _{i}\) is computed as \(\mathsf {P}^{c_{i+1}}(\sigma , pk , sk )\) while for \(i\ge l\) the proof \(\pi _i\) is computed as \(\mathsf {LEval}\left( \omega ,\phi _u,\ ( pk ,c_i,\pi _i)\right) \). Moreover, \(\mathbf {Hyb}_{\rho +1}\) is equivalent to \(\mathbf {G}_1\) while \(\mathbf {Hyb}_{1}\) is equivalent to \(\mathbf {G}_0\).
Suppose there exist a \(\text {PPT}\) adversary \(\mathsf {A}\), an index \(l\in [\rho (\kappa )]\) and a polynomial \(p(\cdot )\) such that, for infinitely many values of \(\kappa \in \mathbb {N}\), the adversary \(\mathsf {A}\) distinguishes between \(\mathbf {Hyb}_l\) and \(\mathbf {Hyb}_{l+1}\) with probability at least \(1/p(\kappa )\).
We can construct an adversary \(\mathsf {B}\) that breaks label derivation privacy. The adversary \(\mathsf {B}\) with input \(\omega \leftarrow \mathsf {I}(1^\kappa )\) runs the code of hybrid \(\mathbf {Hyb}_l\) on \(\mathsf {A}\) until the l-th iteration. At this point \(\mathsf {B}\) forwards to its own challenger the tuple \((\phi _u,c_{l-1}, pk , sk ,\pi _{l-1})\) where \(\phi _u(\cdot ):=\mathsf {UpdateC}( pk ,\cdot \ ;r_u)\) with  , and receives back the proof \(\pi '\). Notice that \(c_{l}:=\phi _u(c_{l-1})\).
, and receives back the proof \(\pi '\). Notice that \(c_{l}:=\phi _u(c_{l-1})\).
If the challenge bit is \(b=0\) then \(\pi '\leftarrow \mathsf {P}^{c_{l}}(\omega , pk , sk )\), and therefore \(\mathsf {B}\) perfectly simulates \(\mathbf {Hyb}_{l+1}\) otherwise if \(b=1\) then \(\pi '\leftarrow \mathsf {LEval}(\omega ,\phi _u, ( pk ,c_{l-1},\pi _{l-1}))\), therefore \(\mathsf {B}\) perfectly simulates \(\mathbf {Hyb}_{l}\). Therefore \(\mathsf {B}\) can break label derivation privacy of \(\mathcal {NIZK}\) with advantage \(1/p(\kappa )\).
Lemma 2
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _{1,2}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_1(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_2(\kappa ) = 1\right] }\right|\le \nu _{1,2}(\kappa )\).
Proof
We reduce to adaptive multi-theorem zero-knowledge of \(\mathcal {NIZK}\).
Suppose there exist a \(\text {PPT}\) adversary \(\mathsf {A}\) and a polynomial p such that, for infinitely many values of \(\kappa \in \mathbb {N}\), \(\left|{\mathbb {P}\left[ \mathbf {G}_1(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_2(\kappa ) = 1\right] }\right|\ge 1/p(\kappa )\). Let \(\mathsf {B}\) be a \(\text {PPT}\) adversary for the multi-theorem zero-knowledge game that runs the same code of \(\mathbf {G}_2\) but for any i, instead of computing the proof \(\pi _i\), forwards to its oracle the query \((c_i, pk , sk )\).
The view provided by \(\mathsf {B}\) to \(\mathsf {A}\) is equivalent to \(\mathbf {G}_2\) if \(\mathsf {B}\)’s oracle is \(\mathsf {P}\) and equivalent to \(\mathbf {G}_3\) if \(\mathsf {B}\)’s oracle is \(\mathcal {SIM}(\tau _{ sim },\cdot )\). Therefore \(\mathsf {B}\) can break multi-theorem zero-knowledge of \(\mathcal {NIZK}\) with advantage \(1/p(\kappa )\).
Lemma 3
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _{2,3}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_2(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_3(\kappa ) = 1\right] }\right|\le \nu _{2,3}(\kappa )\).
Proof
We reduce to the \(\mathcal {T} \)-Malleable label simulation extractability of \(\mathcal {NIZK}\). Let \(\mathsf {Abort}\) be the event that the game \(\mathbf {G}_3\) aborts with message \(\mathbf {Abort}\). Notice that the two games proceed exactly the same until the event \(\mathsf {Abort}\) happens. Therefore, we have
Suppose there exist a \(\text {PPT}\) adversary \(\mathsf {A}\) and a polynomial p such that, for infinitely many values of \(\kappa \in \mathbb {N}\), \({\mathbb {P}\left[ \mathsf {Abort}\right] }\ge 1/p(\kappa )\), where the probability is over the game \(\mathbf {G}_3\) with adversary \(\mathsf {A}\).
Let \(\mathsf {B}\) be a \(\text {PPT}\) adversary for the malleable label simulation extractability that runs the same code of \(\mathbf {G}_3\) but for any i, instead of computing the proof \(\pi _i\), forwards to its oracle the query \((c_i, pk )\) and, if the event during the i-th iteration the message \(\mathbf {Abort}\) is raised, outputs the value \(\tilde{X}_{i+1}^0=(\tilde{ pk },\tilde{c},\tilde{\pi })\). Notice, that the message \(\mathbf {Abort}\) is raised only if the winning condition of the malleable label simulation extractability experiment are met. Therefore the winning probability of \(\mathsf {B}\) is the probability of the event \(\mathsf {Abort}\) in \(\mathbf {G}_3\).
Lemma 4
\({\mathbb {P}\left[ \mathbf {G}_3(\kappa ) = 1\right] }={\mathbb {P}\left[ \mathbf {G}_4(\kappa ) = 1\right] }\).
Proof
Notice that the two games proceed the same until \(\mathsf {PK}(\tilde{ sk })=\mathsf {PK}( sk ')\) but \(\mathsf {Dec}(\tilde{ sk },\tilde{c}) \ne \mathsf {Dec}( sk ',\tilde{c})\). Let \(\mathsf {WrongDec}\) be such event. Then we have
By the correctness of \(E\) we have that the event \(\mathsf {WrongDec}\) has probability 0.
Lemma 5
\({\mathbb {P}\left[ \mathbf {G}_4(\kappa ) = 1\right] }={\mathbb {P}\left[ \mathbf {G}_5(\kappa ) = 1\right] }\).
Proof
Notice that two games proceed the same until \(\phi (c_i)=\tilde{c}\) and \(\phi \in \mathcal {T} \) but \(\mathsf {Dec}( sk ',\tilde{c})\ne m\) (the original message). Let \(\mathsf {NotSame}\) be such event. Therefore, we have
The definition of the set \(\mathcal {T} \) and \(\phi \in \mathcal {T} \) together with the fact that \(c_i\) is an encryption of m under \( pk \) and \(\phi (c_i)=\tilde{c}\) imply that \(\mathsf {Dec}( sk ',\tilde{c})=m\). In fact \(\phi \in \mathcal {T} \) implies that \(\mathsf {Dec}( sk ,\phi (c))\) decrypts correctly if c is a valid ciphertext under \( pk \) and \( pk =\mathsf {PK}( sk )\). Therefore, we have that the event \(\mathsf {NotSame}\) has probability 0.
Lemma 6
\({\mathbb {P}\left[ \mathbf {G}_5(\kappa ) = 1\right] }={\mathbb {P}\left[ \mathbf {G}_6(\kappa ) = 1\right] }\).
Proof
\(\mathbf {G}_6\) does not execute the instruction \(m_{i+1}:=\mathsf {Dec}(\tilde{ sk },\tilde{c})\), however notice that already in game \(\mathbf {G}_5\) either the value \(m_{i+1}\) is overwritten or the game outputs \(\mathbf {Abort}\). So the two game are semantically the same.
Lemma 7
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _{6,7}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_6(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_7(\kappa ) = 1\right] }\right|\le \nu _{6,7}(\kappa )\).
Proof
We reduce to the CLRS security of \(E\) via an hybrid argument. For \(l\in [\rho (\kappa )]\) let \(\mathbf {Hyb}_l\) be an hybrid experiment that executes the code of \(\mathbf {G}_6\) until the \((l-1)\)-th iteration and, after that, executes the code of \(\mathbf {G}_7\). Specifically, for every \(i< l\) the hybrid \(\mathbf {Hyb}_l\), at the i-th iteration, runs the extractor and checks if the conditions \(T'(c)=\tilde{c}\), \(c'\in \{{c}_{0},\ldots ,{c}_{i}\}\) and \(T\in \mathcal {T} \) hold, and, if yes, it sets \(m_{i+1}:=m\). For every \(i\ge l\) the hybrid \(\mathbf {Hyb}_l\), at the i-th iteration, runs the extractor and checks if the conditions \(T'(c)=\tilde{c}\), \(c'=c_i\) and \(T\in \mathcal {T} \) hold, and, if yes, it sets \(m_{i+1}:=m\). In particular, \(\mathbf {Hyb}_0\) is equivalent to \(\mathbf {G}_7\) while \(\mathbf {Hyb}_{\rho }\) is equivalent to \(\mathbf {G}_8\).
Given an adversary \(\mathsf {A}\) and an index \(k\in [l-1]\) define the event \(\mathsf {OldCT}_k\) over the random experiment \(\mathbf {Hyb}_l\) to hold if \(\mathsf {A}\) at the l-th iteration outputs a tampering function \(T_l\) such that \(T_l(X^0_l) = (\tilde{ pk },\tilde{c},\tilde{\pi })\) and, let \((\bot ,T',c')\leftarrow \mathsf {Ext}(\tau _{ ext },\tilde{c},\tilde{\pi })\), then \(c'=c_k\).
Let \(\mathsf {OldCT}\) be the event \(\{\exists k\in [l-1]:\mathsf {OldCT}_k\}\). It is easy to check that
In fact, if the event \(\mathsf {OldCT}\) does not happen in \(\mathbf {Hyb}_l\) then the condition \(c'=c_l\) holds, therefore the two hybrids behave exactly the same.
Suppose there exist an adversary \(\mathsf {A}\) and a polynomial \(p(\cdot )\) such that, for infinitely many values of \(\kappa \in \mathbb {N}\), the adversary \(\mathsf {A}\) distinguishes between game \(\mathbf {G}_6\) and \(\mathbf {G}_7\) with probability at least \(1/p(\kappa )\). Then \({\mathbb {P}\left[ \mathsf {OldCT}\right] }\ge 1/p(\kappa )\).
We build a \(\text {PPT}\) adversary \(\mathsf {B}\) that breaks CLRS Friendly PKE Security of \(E\). Let \(\mathcal {H} \) a family of 2-wise independent hash functions with domain \(\mathcal {C}_E\) and co-domain \(\{0,1\}^\kappa \). We introduce some useful notation in Fig. 5. A formal description of \(\mathsf {B}\) follows:

- 1.
Receive \({ pub }, pk \) from the challenger of the CLRS security experiment and get oracle access to \(\mathcal {O}_\ell (\mathsf {state})\).
- 2.
Set variables \(i,t^0,t^1\) to 0 (as in the \(\mathbf {Tamper}\) experiment).
- 3.
Run \(\omega ,\tau _{ sim },\tau _{ ext }\leftarrow \widetilde{\mathsf {S}}_0(1^\kappa )\), set \( crs := ({ pub },\omega )\) and send \( crs \) to \(\mathsf {A}_0\).
- 4.
Let m, z be the output from \(\mathsf {A}_{0}\), let \(m'\) be a valid plaintext for \(E\) such that the first bit of \(m'\) differs from the first bit of m and \(|m'|=|m|\). Send the tuple \(m,m'\) to the challenger. Set \( st _0:=z\).
- 5.
For \(i=0\) to \((l-1)\) execute the following loop:
- (a)
Sample
and run the adversary \(\mathsf {A}_1(m_i,st_i)\), upon query \((j,L)\) from \(\mathsf {A}_1\), if \(j=1\) forward the same query to the leakage oracle, if \(j=0\) forward the query \((0,\mathbf{L}_{L,r_i, pk })\) to the leakage oracle.
- (b)
Eventually, the adversary \(\mathsf {A}_1\) outputs \((T_{i+1}, st _{i+1},j)\).
- (c)
Forward the query \((1,\mathsf {PK}(T^1_{i+1}(\cdot )))\) to the leakage oracle and let \( pk '\) be the answer. Forward the query \((0,\mathbf{V}_{T^0_{i+1},r_i, pk , pk '})\) to the leakage oracle and let a be the answer, if \(a=0\) then set \(m_{i+1}:=\bot \) and continue to the next cycle.
- (d)
Otherwise, forward the query \((0,\mathbf{M}_{T_{i+1},r_i, pk })\) and let \(m'\) be the answer, if \(m'\) is Abort \(^*\) then abort, otherwise set \(m_{i+1}:=m'\). Execute the refresh algorithm \(\mathsf {Rfrsh}^*(j)\) as defined by \(\mathbf {G}_6\). (In particular, use the trapdoor \(\tau _{ sim }\) to sample \(\pi _{i+1}\leftarrow \widetilde{\mathsf {S}}_1(\tau _{ sim },c_{i+1}, pk )\).)
- 6.
Sample
and
and run the adversary \(\mathsf {A}_1\) on input \((m_{l-1}, st _{l-1}\)) and reply to the leakage oracle queries as in step (5a). Eventually, the adversary \(\mathsf {A}_1\) outputs \((T_{l}, st _l,j)\) forward the leakage query \((0,\mathbf{H}_{T_l,r_l, pk ,H})\), let h be the answer of the leakage oracle.
- 7.
Set x to be the empty string. For \(i:=1\) to \(\eta \), where \(\eta :=2p^2(\kappa )+2p(\kappa )|c|\), execute the following:
- (a)
Sample
and run the adversary \(\mathsf {A}_1\) on input \((m_{l-1}, st _{l-1}\)) and reply to the leakage oracle queries as in step (5a).
- (b)
Eventually the adversary \(\mathsf {A}_1\) outputs \((T_{l}, st _l,j)\), forward the query \((0,\mathbf{H}_{T_l,r, pk ,x})\) to the leakage oracle, let a the answer, if \(a\ne \bot \) set \(x:= x\Vert a\).
- (c)
Call the oracle \(\mathsf {Update}(0)\) and increase the counter i.
- 8.
If \(|x|<|c|\) then sample
and output \(b'\). Otherwise, query the leakage oracle with \((1,\left( \mathsf {Dec}(\cdot ,x)\right) _{(0)})\) and let a be the answer. If \(a=m_{(0)}\) output 0 else output 1.
We compute the amount of leakage performed by \(\mathsf {B}\). For any executions of the loop in step (5) the adversary \(\mathsf {B}\) forwards all the leakage queries made by \(\mathsf {A}\) and, additionally:
-
In step (5c) leaks \(\log |\mathcal {PK}|\) bits from the secret key and 1 bit from the ciphertext;
-
In step (5d) leaks \(\log (|\mathcal {M}|+2)\) bits from the ciphertext (the output is either a message or \(*\) or \(\mathbf {Abort}\));
Notice that \(\tau \) many of the leakage queries described above are allowed before an invocation of \(\mathsf {Update}\) is forced. Moreover, in step (6) the adversary \(\mathsf {B}\) leaks \(\kappa \) bit from the ciphertext and for any executions of the loop in step (7) leaks 1 bit from the ciphertext and then it calls the \(\mathsf {Update}\) algorithm.
Let \(\ell _\mathsf {A}\) the maximum amount of leakage between each invocation of the \(\mathsf {Rfrsh}^*\) algorithm done by \(\mathsf {A}\), then the amount of leakage done by \(\mathsf {B}\) is:
We compute the winning probability of \(\mathsf {B}\). Let \({c}_{0},\ldots ,{c}_{l+\eta }\) be the set of ciphertexts produced (either by \(\mathsf {Enc}\), in the case of \(c_0\), or by the \(\mathsf {UpdateC}\) procedure otherwise) during the CLRS Security Experiment with \(\mathsf {B}\). Consider the following events and random variables:
-
Let \(\mathsf {Collision}\) be the event \(\{ \exists i,j \le [l+\eta ]: i\ne j \wedge H(c_i)=H(c_j)\}\);
-
Let \(\mathsf {Hit}\) be the event that \(\{ \exists k < l: h=H(c_{k}) \}\), where h is the output of the leakage query \((0,\mathbf{H}_{T_l,r_l, pk ,H})\) (see step 6).
-
Let \(\mathsf {Hit}_i\) be the random variable equal to 1 if the condition \(\left( h=H(c)\right) \) in the i-th execution of the leakage query \((0,\mathbf{H}_{T_l,r_{l+i}, pk ,x})\) (see step 7) holds, 0 otherwise.
-
Let \(\mathsf {Complete}\) be the event \(|x|=|c|\).
It is easy to check that if \(\left( \lnot \mathsf {Collision}\wedge \mathsf {Hit}\wedge \mathsf {Complete}\right) \) holds then, at step (8), there exist a positive index \(k< l\) such that \((x=c_{k})\) holds. Therefore conditioned on the conjunction of the events the adversary \(\mathsf {B}\) winsFootnote 3 with probability 1.
Claim
\({\mathbb {P}\left[ \mathsf {Collision}\right] }\le (\eta +l)^2\cdot 2^{-\kappa }\).
Proof
Recall that H is 2-wise independent, therefore for any fixed \(x,y\in \mathcal {C}_E\) such that \(x\ne y\), \({\mathbb {P}\left[ H(x)=H(y)\right] }=2^{-\kappa }\), where the probability is taken over the sampling of H. Moreover, the ciphertexts \(c_i\) for \(i\in [l+\eta ]\) are sampled independently of the choice of H, therefore given two indices i, j where \(i\ne j\), by averaging over all the possible assignment of \(c_i,c_j\) we have that \({\mathbb {P}\left[ H(c_i)=H(c_j)\right] }=2^{-\kappa }\). By union bound we get the claim.
Claim
\({\mathbb {P}\left[ \mathsf {Hit}~|~{b=0}\right] }={\mathbb {P}\left[ \mathsf {OldCT}\right] }\).
Proof
In fact, the adversary \(\mathsf {B}\) (on challenge the ciphertext \(\mathsf {Enc}( pk ,m)\)) follows the code of \(\mathbf {Hyb}_l\) until step 6. In particular, \(\mathsf {B}\) has only oracle access to the ciphertext and the secret key (as prescribed by the CLRS Security experiment), while the hybrid \(\mathbf {Hyb}_l\) has full access to them. However, the adversary \(\mathsf {B}\) can perform the same operations via its own leakage oracle access. Therefore, in the execution of the leakage query \((0,\mathbf{H}_{T_l,r_l, pk ,H})\) at step (6), the event \(c'=c_{k}\) where \( sk ',T',c'\leftarrow \mathsf {Ext}(\tau _{ ext },\tilde{ pk })\) holds with the same probability of the event \(\mathsf {OldCT}\) in the hybrid \(\mathbf {Hyb}_l\).
Claim
\({\mathbb {P}\left[ \mathsf {Complete}\right] }\le 2^{-2\kappa +1}\).
Proof
Let \(\varphi \) be the variable that denotes all the randomness used (including the challenger randomness) in the CLRS experiment between the challenger and the adversary \(\mathsf {B}\) just before the execution of the step 7. Let \(\mathsf {Good}\) the event that \(\left\{ {\mathbb {P}\left[ \mathsf {Hit}\right] } \ge 1/2p(\kappa ) \right\} \). By a Markov argument the probability \({\mathbb {P}\left[ \varphi \in \mathsf {Good} \right] }\) is at least 1/2. We can condition on the event \(\mathsf {Good}\).
We analyze the random variables \(\{\mathsf {Hit}_i\}_{i\in [\eta ]}\). Fixing the choice of the randomness \(\varphi \), for any i, the random variable \(\mathsf {Hit}_i\) depends only on \(r_{l+i}\) and on the output of \(\mathsf {UpdateC}\) at the \((l+i)\)-th invocation. Notice that the adversary \(\mathsf {B}\) at each iteration of step 7 samples a fresh \(r_{l+i}\), moreover by the perfectly ciphertext-update privacy (see Definition 5) of \(E\), for any \(j\ne i\) the ciphertext \(c_i\) and \(c_j\) are independent (in fact, for any k the distribution of \(c_{k+1}\) does not depend on the value of \(c_{k}\)). Therefore, the random variables \(\{\mathsf {Hit}_i\}_{i\in [\eta ]}\) for any assignment of \(\varphi \) are independent. Let \(Z:=\sum _{j\in [\eta ]}\mathsf {Hit}_j\), we have that \(\mathbb {E} _{}\left[ Z~|\mathsf {Good} \right] \ge \eta /2p(\kappa )\).
Where, in the last step of the above disequations, we used the Chernoff bound.
Let \(\mathsf {Guess}:=(\lnot \mathsf {Hit}\vee \lnot \mathsf {Complete})\), namely the event that triggers \(\mathsf {B}\) to guess the challenge bit at random. Obviously, for any \(a\in \{0,1\}\), \({\mathbb {P}\left[ b'=b~|~\mathsf {Guess},b=a\right] }=\frac{1}{2}\). For any \(a\in \{0,1\}\) and infinitely many \(\kappa \):
Where Eq. (1) follows because \({\mathbb {P}\left[ b'=b~|~\lnot \mathsf {Collision}\wedge \mathsf {Hit}\wedge \mathsf {Complete}\right] }=1\) and Eq. (2) follows because \({\mathbb {P}\left[ \mathsf {Guess}\right] }\ge 1-{\mathbb {P}\left[ \mathsf {Hit}\right] }\).
Lemma 8
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _{7,8}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_7(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_8(\kappa ) = 1\right] }\right|\le \nu _{7,8}(\kappa )\).
Proof
We reduce to the CLRS Friendly PKE Security of \(E\).
By contradiction, assume that there exists a PPT an adversary and a polynomial \(p(\cdot )\) such that for infinitely many values of \(\kappa \in \mathbb {N}\), we have that \(\mathsf {A}\) distinguishes between game \(\mathbf {G}_7\) and game \(\mathbf {G}_8\) with probability at least \(1/p(\kappa )\). We build a \(\text {PPT}\) adversary \(\mathsf {B}\) that breaks CLRS Friendly PKE Security of \(E\). The adversary \(\mathsf {B}\) follows the points (1) to (5) of the adversary defined in Lemma 7 with the following modifications: (i) The adversary \(\mathsf {B}\) runs internally \(\mathsf {D}\); (ii) The messages for the challenge are m and \(0^\kappa \); (iii) The cycle in step (5) runs for \(i=0\) to \(\rho (\kappa )\); (iv) The adversary \(\mathsf {B}\) eventually outputs the same output bit as \(\mathsf {A}\). Let \(\ell _\mathsf {A}\) the maximum amount of leakage between each invocation of the \(\mathsf {Rfrsh}^*\) algorithm done by \(\mathsf {A}\), then the amount of leakage done by \(\mathsf {B}\) is:
A formal description of \(\mathsf {B}\) follows.

- 1.
Receive \({ pub }, pk \) from the challenger of the CLRS security experiment and get oracle access to \(\mathcal {O}_\ell (\mathsf {state})\).
- 2.
Set variables \(i,\mathsf {flg},l^0,l^1,t^0,t^1\) to 0 (as in the \(\mathbf {Tamper}\) experiment).
- 3.
Run \(\omega ,\tau _{ sim },\tau _{ ext }\leftarrow \widetilde{\mathsf {S}}_0(1^\kappa )\), set \( crs := ({ pub },\omega )\) and send \( crs \) to \(\mathsf {A}_0\).
- 4.
Let m, z be the output from \(\mathsf {A}_{0}\). Send \((m,0^\kappa )\) to the challenger and set \( st _0:=z\).
- 5.
For \(i=0\) to \(\rho (\kappa )\) execute the following loop:
- (a)
Sample
and run the adversary \(\mathsf {A}_1(m_i,st_i)\), upon query \((j,L)\) from \(\mathsf {A}_1\), if \(j=1\) forward the same query to the leakage oracle, if \(j=0\) forward the query \((0,\mathbf{L}_{L,r_i, pk })\) to the leakage oracle.
- (b)
Eventually, the adversary \(\mathsf {A}_1\) outputs \((T_{i+1}, st _{i+1},j)\).
- (c)
Forward the query \((1,\mathsf {PK}(T^1_{i+1}(\cdot )))\) to the leakage oracle and let \( pk '\) be the answer. Forward the query \((0,\mathbf{V}_{T^0_{i+1},r_i, pk , pk '})\) to the leakage oracle and let a be the answer, if \(a=0\) then set \(m_{i+1}:=\bot \) and continue to the next cycle.
- (d)
Otherwise, forward the query \((0,\mathbf{M}_{T_i,r_i, pk })\) and let \(m'\) be the answer, if \(m'\) is Abort \(^*\) then abort, otherwise set \(m_{i+1}:=m'\).
- (e)
Execute the refresh algorithm \(\mathsf {Rfrsh}^*(j)\) as defined by \(\mathbf {G}_6\). (In particular, use the trapdoor \(\tau _{ sim }\) to sample \(\pi _{i+1}\leftarrow \widetilde{\mathsf {S}}_1(\tau _{ sim },c_{i+1}, pk )\).)
- 6.
Output \(\mathsf {A}_2( st _{\rho })\).
The view provided by \(\mathsf {B}\) to \(\mathsf {A}\) is equivalent to \(\mathbf {G}_7\) if the challenge bit b of the PKE Friendly Security experiment is 0. (This because the encrypted message is m.) Otherwise the view is equivalent to \(\mathbf {G}_8\).
Wrapping up all together we have that:
5 Concrete Instantiations
For a group \(\mathbb {G}\) of prime order q and a generator g of \(\mathbb {G}\), we denote by \([a]_g:=g^a\in \mathbb {G}\) the implicit representation of an element \(a\in \mathbb {Z}_q\). Let \(\mathcal {G} \) be a \(\text {PPT}\) pairing generation algorithm that upon input the security parameter \(1^\kappa \) outputs a tuple \(gd=(\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,q,g,h,e)\) where the first three elements are the description of groups of prime order \(q>2^{\kappa }\), g (resp. h) is a generator for the group \(\mathbb {G}_1\) (resp. \(\mathbb {G}_2\)) and e is an efficiently computable non-degenerate pairing function from \(\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T\). In what follow, we indicate vectors with bold chars and matrices with capital bold chars, all vectors are row vectors, given a group \(\mathbb {G}\), two matrices \({\varvec{X}}\in \mathbb {G}^{n\times m}, {\varvec{Y}}\in \mathbb {G}^{m\times t}\) for \(n,m,t\ge 1\) and an element \(a\in \mathbb {G}\) we denote with \({\varvec{X}} \cdot {\varvec{Y}}\) the matrix product of \({\varvec{X}}\) and \({\varvec{Y}}\) and with \(a\cdot {\varvec{X}}\) the scalar multiplication of \({\varvec{X}}\) by a. Given two elements \([a]_g\in \mathbb {G}_1\) and \([b]_h\in \mathbb {G}_2\) we denote with \([a]_g\bullet [b]_h=[a\cdot b]_{e(g,h)}\) the value \(e([a]_g,[b]_h)\), the notation is extended to vectors and matrices in the natural way. Given a field \(\mathbb {F}\) and natural numbers \(n,m,j\in \mathbb {N}\) where \(j\le \min (n,m)\) we define \(\mathsf {Rk}_j(\mathbb {F}^{n\times m})\) to be the set of matrices in \(\mathbb {F}^{n\times m}\) with rows rank j; given a matrix \({\varvec{B}}\) we let \(\mathsf {Rank}({\varvec{B}})\) be the rank of \({\varvec{B}}\).
Definition 7
The k-rank hiding assumption for a pairing generation algorithm  states that for any \(i\in \{1,2\}\) and for any \(k\le j,j'\le \min (n,m)\) the tuple \((g_i,[{\varvec{B}}]_{g_i})\) and the tuple \((g_i,[{\varvec{B}}']_{g_i})\) for random
states that for any \(i\in \{1,2\}\) and for any \(k\le j,j'\le \min (n,m)\) the tuple \((g_i,[{\varvec{B}}]_{g_i})\) and the tuple \((g_i,[{\varvec{B}}']_{g_i})\) for random  and
and  are computational indistinguishable.
are computational indistinguishable.
The k-rank hiding assumption was introduced by Naor and Segev in [37] where the authors showed to be implied by the more common k-linear (DLIN) assumption. The assumption gets weaker as k increases. In fact for \(k=1\) this assumption is equivalent to DDH assumption. Unfortunately, it is known that DDH cannot hold in symmetric pairings where \(\mathbb {G}_1=\mathbb {G}_2\). However, it is reasonable to assume that DDH holds in asymmetric pairings. This assumption is often called external Diffie-Hellman assumption (SXDH) (see [4, 9]).
5.1 The Encryption Scheme
We consider a slight variation of the CLRS Friendly PKE scheme of [18]. Consider the following PKE scheme \(E= (\mathsf {Setup},\mathsf {Gen},\mathsf {Enc},\mathsf {Dec},\mathsf {UpdateC},\mathsf {UpdateS})\) with message space \(\mathcal {M}:= \{0,1\}\) and parameters \(n,m,d\in \mathbb {N}\).
-
 Sample \(gd\leftarrow \mathcal {G} (1^\kappa )\) and vectors
Sample \(gd\leftarrow \mathcal {G} (1^\kappa )\) and vectors  such that \({\varvec{p}} \cdot {\varvec{w}}^T=0\mod q\). Return \({ pub }:= (gd,[{\varvec{p}}]_g,[{\varvec{w}}]_h)\). (Recall that all algorithms implicitly take \({ pub }\) as input.)
such that \({\varvec{p}} \cdot {\varvec{w}}^T=0\mod q\). Return \({ pub }:= (gd,[{\varvec{p}}]_g,[{\varvec{w}}]_h)\). (Recall that all algorithms implicitly take \({ pub }\) as input.) -
 Sample
Sample  ,
, 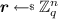 and compute \( sk := [{\varvec{r}}^T\cdot {\varvec{w}} + {\varvec{1}}_n^T \cdot {\varvec{t}}]_h\), set \(\alpha := {\varvec{p}} \cdot {\varvec{t}}^T\) and compute \( pk :=[\alpha ]_g\). The latter can be computed given only \([{\varvec{p}}]_g\in \mathbb {G}_1^m\) and \({\varvec{t}}\in \mathbb {Z}_q^m\). Return \(( pk , sk )\).
and compute \( sk := [{\varvec{r}}^T\cdot {\varvec{w}} + {\varvec{1}}_n^T \cdot {\varvec{t}}]_h\), set \(\alpha := {\varvec{p}} \cdot {\varvec{t}}^T\) and compute \( pk :=[\alpha ]_g\). The latter can be computed given only \([{\varvec{p}}]_g\in \mathbb {G}_1^m\) and \({\varvec{t}}\in \mathbb {Z}_q^m\). Return \(( pk , sk )\). -
 Sample
Sample  and compute \(c_1:=[{\varvec{u}}^T\cdot {\varvec{p}}]_g\) and \(c_2:=[\alpha {\varvec{u}}+b{\varvec{1}}_n]_g\). Return \(C:=(c_1,c_2)\).
and compute \(c_1:=[{\varvec{u}}^T\cdot {\varvec{p}}]_g\) and \(c_2:=[\alpha {\varvec{u}}+b{\varvec{1}}_n]_g\). Return \(C:=(c_1,c_2)\). -
 Let \(f=e(g,h)\), parse \( sk = [{\varvec{S}}]_h\in \mathbb {G}_2^{n\times m}\), let \({\varvec{S}}_1\) be the first row of \({\varvec{S}}\) and parse \(C=([{\varvec{C}}]_g,[{\varvec{c}}]_g)\in \left( \mathbb {G}_1^{n\times m}\times \mathbb {G}_1^{n}\right) \). Compute \({\varvec{b}}:=[{\varvec{c}} - {\varvec{C}} \cdot {\varvec{S}}_1^T ]_f\) and output 1 if and only if \({\varvec{b}} = [{\varvec{1}}_n]_f\). In particular, \([{\varvec{b}}]_f\) can be computed by first computing \([{\varvec{c}}]_f:=e([{\varvec{c}}]_g,h)\) and then \([{\varvec{C}}\cdot {\varvec{S}}_1^T]_f:=\prod _i e({\varvec{C}}[i],{\varvec{S}}[i])\).
Let \(f=e(g,h)\), parse \( sk = [{\varvec{S}}]_h\in \mathbb {G}_2^{n\times m}\), let \({\varvec{S}}_1\) be the first row of \({\varvec{S}}\) and parse \(C=([{\varvec{C}}]_g,[{\varvec{c}}]_g)\in \left( \mathbb {G}_1^{n\times m}\times \mathbb {G}_1^{n}\right) \). Compute \({\varvec{b}}:=[{\varvec{c}} - {\varvec{C}} \cdot {\varvec{S}}_1^T ]_f\) and output 1 if and only if \({\varvec{b}} = [{\varvec{1}}_n]_f\). In particular, \([{\varvec{b}}]_f\) can be computed by first computing \([{\varvec{c}}]_f:=e([{\varvec{c}}]_g,h)\) and then \([{\varvec{C}}\cdot {\varvec{S}}_1^T]_f:=\prod _i e({\varvec{C}}[i],{\varvec{S}}[i])\). -
 Parse \(C=([{\varvec{C}}]_g,[{\varvec{c}}]_g)\in \left( \mathbb {G}_1^{n\times m}\times \mathbb {G}_1^{n}\right) \). Sample
Parse \(C=([{\varvec{C}}]_g,[{\varvec{c}}]_g)\in \left( \mathbb {G}_1^{n\times m}\times \mathbb {G}_1^{n}\right) \). Sample  such that \({\varvec{B}}\cdot {\varvec{1}}_n^T={\varvec{1}}_n\) and the rank of \({\varvec{B}}\) is d. Return \(([ {\varvec{B}} \cdot {\varvec{C}}],[{\varvec{B}} \cdot {\varvec{c}}^T])\).
such that \({\varvec{B}}\cdot {\varvec{1}}_n^T={\varvec{1}}_n\) and the rank of \({\varvec{B}}\) is d. Return \(([ {\varvec{B}} \cdot {\varvec{C}}],[{\varvec{B}} \cdot {\varvec{c}}^T])\). -
 Parse \( sk =[{\varvec{S}}]_h\in \mathbb {G}_2^{n\times m}\). Sample
Parse \( sk =[{\varvec{S}}]_h\in \mathbb {G}_2^{n\times m}\). Sample  such that \({\varvec{A}}\cdot {\varvec{1}}_n^T={\varvec{1}}_n\) and the rank of \({\varvec{A}}\) is d. Return \([ {\varvec{A}} \cdot {\varvec{S}}]_h\).
such that \({\varvec{A}}\cdot {\varvec{1}}_n^T={\varvec{1}}_n\) and the rank of \({\varvec{A}}\) is d. Return \([ {\varvec{A}} \cdot {\varvec{S}}]_h\).
Some remarks are in order. First, the main difference between the scheme above and the PKE of [18] is in the public-keys and in the ciphertexts spaces. Let \(E_{\mathsf {DLWW}}\) be the scheme proposed by [18]. A public key for \(E_{\mathsf {DLWW}}\) is the target group element \([{\varvec{p}} \cdot {\varvec{t}}^T]_f\), while in the scheme above, a public key belongs to the group \(\mathbb {G}_1\). Similarly, a ciphertext for \(E_{\mathsf {DLWW}}\) is a tuple \((c_1,c_2)\) where \(c_2\in \mathbb {G}_T^n\). The message space of \(E_{\mathsf {DLWW}}\) is \(\mathbb {G}_T\), while the message space of the scheme above is \(\{0,1\}\). This is a big disadvantage, however, thanks to this modification, the public keys, secret keys and ciphertexts belong either to \(\mathbb {G}_1\) or \(\mathbb {G}_2\). As we will see, this modification is necessary to use lM-NIZK based on Groth-Sahai proof systems [30].
Second, we cannot directly derive from the secret key the public key. However, we can define the function \(\mathsf {PK}'\) that upon input \( sk =[{\varvec{S}}]_h\) produces \( pk ' = [{\varvec{p}}]_g \bullet [{\varvec{S}}_1 ]_h \), where \({\varvec{S}}_1\) is the first row of \({\varvec{S}}\). Notice that the NMC \(\varSigma \) and the simulator \(\mathsf {S}_1\) of Theorem 1 need to check if the public key stored in one side is valid for the secret key stored in the other side. We can fixFootnote 4 this issue by checking the condition \(e( pk ,h)=\mathsf {PK}'( sk )\) instead.
Theorem 2
For any \(m\ge 6, n\ge 3m-6, d:=n-m+3\) the above scheme is an \(\ell \)-CLRS-friendly encryption scheme under the External Diffie-Hellman Assumption on \(\mathcal {G} \) for \(\ell =\min \{m/6-1,n-3m+6\}\cdot \log (q)-\omega (\log \kappa )\).
The proof of security follows the same line of [18]. The PKE scheme \(E\) is perfectly ciphertext-update private. See the full version [23] of the paper for more details.
Unfortunately, the message space of the PKE is \(\{0,1\}\) which limits the number of applications of NMC-R. We propose two different way to overcome this weakness:
-
For any \(k\in \mathbb {N}\) let \(E^{\times k}\) the direct product encryption scheme that given a message in \(\{0,1\}^\kappa \) encrypts it bit by bit. In the full version of the paper we show that if \(E\) is a \(\ell \)-CLRS-Friendly secure PKE then \(E^{\times k}\) is a \(\ell \)-CLRS-Friendly secure PKE. Unfortunately, the leakage-rate of the encoding scheme gets much worse. In fact, the size of the chipertexts increase \(\kappa \) times but the leakage parameter stays the same.
-
We define CLRS-Friendly Key Encapsulation Mechanisms and the Non-Malleable Key-Encoding schemes with Refresh. The latter notion is strictly weaker than Non-Malleable Codes, however, it still allows useful applications in the setting of tamper resilience cryptography. We defer all the details to the full version of the paper.
5.2 The Label-Malleable NIZK
We can cast a lM-NIZK as a special case of the Controlled-Malleable NIZK (cM-NIZK) argument of knowledge systems [10]. Roughly speaking, cM-NIZK systems allow malleability (from a specific set of allowable transformation) both on the instance and on the NIZK proof. Similarly to lM-NIZK AoK systems, cM-NIZK systems have a form of simulation sound extractability called Controlled-Malleable Simulation Sound Extractability (cM-SSE). Informally, the extractor will either extract a valid witness or will track back to a tuple formed by an instance queried to the simulation oracle and the associated simulated proof.
The elegant framework of [10] (full version [11]) builds on the malleability of Groth-Sahai proof systems [30] and provides a set of sufficient conditions to have efficient cM-NIZK systems. Here we translate the conditions to the setting of lM-NIZK systems.
Definition 8
For a relation \(\mathcal {R}\) and a set of transformations \(\mathcal {T}\) on the set of labels \(\mathcal L\), we say \((\mathcal {R}, \mathcal {T})\) is LM-friendly if the following five properties hold:
-
1.
Representable statements and labels: any instance and witness of \(\mathcal {R}\) can be represented as a set of group elements; i.e., there are efficiently computable bijections \(F_s : L_{\mathcal {R}} \rightarrow \mathbb {G}_{i_s}^{d_s}\) for some \(d_s\) and \(i_s\), \(F_w :W_\mathcal {R}\rightarrow G_{i_d}^{d_w}\) for some \(d_w\) and \(i_w\) where \(L_\mathcal {R}:=\{ x | \exists w: (x,w)\in \mathcal {R}\}\) and \(L_\mathcal {R}:=\{ w | \exists x: (x,w)\in \mathcal {R}\}\) and \(F_l : \mathcal L\rightarrow \mathbb {G}_{i_l}^{d_l}\) for some \(d_l\) and \(i_l=i_s\).
-
2.
Representable transformations: any transformation in \(\mathcal {T}\) can be represented as a set of group elements; i.e., there is an efficiently computable bijection \(F_t : \mathcal {T}\rightarrow G^{d_t}_{i_t}\) for some \(d_t\) and some \(i_t\).
-
3.
Provable statements: we can prove the statement \((x,w) \in \mathcal {R}\) (using the above representation for x and w) using pairing product equations; i.e., there is a pairing product statement that is satisfied by \(F_s(x)\) and \(F_w(w)\) iff \((x,w) \in ~\mathcal {R}\).
-
4.
Provable transformations: we can prove the statement “\(\phi (L') = L \wedge \phi \in \mathcal {T}\)” (using the above representations for labels \(L,L'\) and transformation \(\phi \)) using a pairing product equation, i.e. there is a pairing product statement that is satisfied by \(F_t(\phi ),F_l(L),F_l(L')\) iff \(T \in \mathcal {T}\wedge \ \phi (L') = L\).
-
5.
Transformable transformations: for any \(\phi ,\phi ' \in \mathcal {T}\) there is a valid transformation \(t(\phi )\) that takes the statement “\(\phi (L') = L \wedge \ \phi \in \mathcal {T}\)” (phrased using pairing products as above) for the statement “\((\phi '\circ \phi )(L') = \phi (L) \wedge \ (\phi '\circ \phi ) \in \mathcal {T}\)” and that preservesFootnote 5 the label \(L'\).
The definition above is almost verbatim from [11], the only differences are that the point (1) is extended to support labels and that the original definition has a condition on the malleability of the tuple statement/witness (which trivially holds for lM-NIZK). We adapt a theorem of [11] to the case of Label Malleability:
Theorem 3
If the DLIN assumption holds then we can construct a lM-NIZK that satisfies derivation privacy for any LM-friendly relation and transformation set \((\mathcal {R},\mathcal {T})\).
With this powerful tool in our hand, we are now ready to show that there exists a lM-NIZK for the relation and transformation set \((\mathcal {R} _{ pub },\mathcal {T} _{ pub })\) defined above:
where \({ pub }=(gd,[{\varvec{p}}]_g,[{\varvec{w}}]_h)\leftarrow \mathsf {Setup}(1^\kappa )\). Notice that the set of all the possible updates of a ciphertext,
is a subset of \(\mathcal {T}_{ pub }\). Therefore, we can apply the generic transformation of Sect. 4 given a lM-NIZK for the relation \(\mathcal {R}_{ pub }\) and the set of transformations \(\mathcal {T}_{ pub }\) and the CLRS-Friendly PKE defined above. We show that the tuple \((\mathcal {R} _{ pub },\mathcal {T} _{ pub })\) is LM-Friendly.
-
Representable statements and labels: Notice that \(L_{\mathcal {R}_{ pub }}\subseteq \mathbb {G}_1\), while the set of valid label is the set \(\mathbb {G}_1^{n\times m}\times \mathbb {G}_1^{n}\).
-
Representable transformations: We can describe a transformation \(\phi _{{\varvec{B}}}\in \mathcal {T}_{ pub }\) as a matrix of elements \([{\varvec{B}}]_h\in \mathbb {G}_2^{n\times n}\).
-
Provable statements: The relation \(\mathcal {R}_{ pub }\) can be represented by the pairing product statement \([\alpha ]_g\bullet [1]_h = [{\varvec{p}}] \bullet [{\varvec{S}}_1^T]_h\).
-
Provable transformations: Given a transformation \(\phi _{{\varvec{B}}}\in \mathcal {T}_{ pub }\) and labels \(c=([{\varvec{C}}]_g,[{\varvec{c}}]_g),c'=([{\varvec{C}}']_g,[{\varvec{c}}']_g)\), the statement “\(\phi _{{\varvec{B}}}(c') = c \wedge \phi _{{\varvec{B}}} \in \mathcal {T}\)” is transformed as the system of pairing product statements:
$$\begin{aligned} \left\{ \begin{array}{l} \ [{\varvec{B}}]_h \bullet [{\varvec{C}}'^T]_g = [{\varvec{C}}]_g\bullet [1]_h \\ \ [{\varvec{B}}]_h \bullet [{\varvec{c}}'^T]_g = [{\varvec{c}}]_g\bullet [1]_h \\ \ [{\varvec{B}}]_h \bullet [{\varvec{1}}^T]_g = [{\varvec{1}}]_f \end{array} \right. \end{aligned}$$(3) -
Transformable transformations: Let \(\phi _{{\varvec{B}}},c,c'\) be as before and let \(\phi _{{\varvec{B}}'}\in \mathcal {T}_{ pub }\). We show that we can transform the system in Eq. (3) to be a valid system of pairing product statement for the statement \((\phi _{{\varvec{B}}'}\circ \phi _{{\varvec{B}}})(c') = \phi _{{\varvec{B}}'}(c) \wedge (\phi _{{\varvec{B}}'}\circ \phi _{{\varvec{B}}}) \in \mathcal {T}\). Given the system of pairing product equations in Eq. (3) and \({\varvec{B}}'\in \mathbb {Z}_q^{n\times n}\) we can perform operations at the exponent and derive:
$$\begin{aligned} \left\{ \begin{array}{l} \ [{\varvec{B}}'\cdot {\varvec{B}}]_h \bullet [{\varvec{C}}'^T]_g = [{\varvec{B}}'\cdot {\varvec{C}}^T]_g\bullet [1]_h \\ \ [{\varvec{B}}'\cdot {\varvec{B}}]_h \bullet [{\varvec{c}}'^T]_g = [{\varvec{B}}'\cdot {\varvec{c}}^T]_g\bullet [1]_h \\ \ [{\varvec{B}}'\cdot {\varvec{B}}]_h \bullet [{\varvec{1}}^T]_g = [{\varvec{1}}]_f \end{array} \right. \end{aligned}$$
The Set \({\varvec{\mathcal {T}}}_{{\varvec{pub}}}^{\times {{\varvec{k}}}}\) of Transformations for \({{\varvec{E}}}^{\times {{\varvec{k}}}}\) . For any \(k\in \mathbb {N}\), let the PKE scheme \(E^{\times k}\) be defined as in Sect. 5.1, let \(\mathcal {C}_{E^{\times k}}=(\mathcal {C}_{E})^k\) be the ciphertexts space of \(E^{\times k}\) and let \(\mathcal {T}_{ pub }^{\times k} = (\mathcal {T}_{ pub })^{k}\). Explicitly, the set of transformations is defined as:
For any positive polynomial \(k(\kappa )\), the tuple \((\mathcal {R}_{ pub },\mathcal {T}_{ pub }^{\times k})\) is LM-Friendly. The result follows straight forward from the framework presented in Sect. B.3 of [11] where it is shown that the for any pair of transformations on statements over pairing product equations we can derive a new transformation for the conjunction of the statements.
6 Applications
Following the same approach of [22, 34] we show a compiler that maps any functionality \(G(s,\cdot )\) to a Continually-Leakage-and-Tamper Resilient functionality \(G'(s',\cdot )\) equipped with refresh procedure \(\mathsf {Rfrsh}\). Consider the experiments in Fig. 6.
Definition 9
A compiler \(\varPhi =(\mathsf {Setup},\mathsf {FCompile}, \mathsf {MCompile},\mathsf {Rfrsh})\) is a Split-State \((\ell ,\rho ,\tau )\)-Continually-Leakage-and-Tamper (for short \((\ell ,\rho ,\tau )\)-CLT) Compiler in the CRS model if for every \(\text {PPT}\) adversary \(\mathsf {A}\) there exists a simulator \(\mathsf {S}\) such that for every efficient functionality \(G:\{0,1\}^\kappa \times \{0,1\}^i\rightarrow \{0,1\}^o\) for \(\kappa ,i,o\in \mathbb {N}\) and any secret state \(s\in \{0,1\}^\kappa \), the output of the real experiment \(\mathbf {TamperFunc}^{(G,s)}_{\mathsf {A},\varPhi }(\kappa ,\ell ,\rho ,\tau )\) and the output of the simulated experiment \(\mathbf {IdealFunc}(\kappa )\) are indistinghuishable.
Given a NMC-R \(\varSigma \), consider the following compiler \(\varPi = (\mathsf {Setup},\mathsf {MCompile},\mathsf {Enc},\mathsf {FCompile},\mathsf {Rfrsh})\):
-
 Output
Output  ;
; -
 Output
Output  ;
; -
 Output \(G'(s',x):=G(\varSigma .\mathsf {Dec}( crs ,s'))\);
Output \(G'(s',x):=G(\varSigma .\mathsf {Dec}( crs ,s'))\); -
 Output \(\varSigma .\mathsf {Rfrsh}( crs ,s')\).
Output \(\varSigma .\mathsf {Rfrsh}( crs ,s')\).
Theorem 4
Let \(\varSigma \) be a \((\ell ,\rho ,\tau )\)-Non-Malleable Code with Refresh then \(\varPi \) as defined above is a Split-State \((\ell ,\rho ,\tau )\)-CTL Compiler in the CRS model.
Notes
- 1.
Notice that tampering does not overwrite the codeword. This is called non-persistent tampering and is stronger than persistent tampering in the split state model as the set of tampering functions is closed under composition—subsequent tamperings can just first reapply all previous tampering functions (cf. Jafargholi and Wichs [32]).
- 2.
We also are assuming that the NIZK system is not succinct.
- 3.
Notice we assume perfect correctness of \(E\).
- 4.
In particular, the reduction in Lemma 7 in steps 5c can leak \((1,\mathsf {PK}'(T_{i+1}(\cdot )))\) and then, in step 5d, we need to modify the function \(\mathbf{V}_{T^0_{i+1},r_i, pk , pk '}\) to check if \(e(\tilde{ pk },h)= pk '\) and the function \(\mathbf{M}_{T_{i+1},r_i, pk }\) to check if \(e(\tilde{ pk },h)=\mathsf {PK}'( sk ')\).
- 5.
See full version for the formal definition.
References
Aggarwal, D., Dodis, Y., Lovett, S.: Non-malleable codes from additive combinatorics. In: Proceedings of the STOC, pp. 774–783 (2014)
Agrawal, S., Gupta, D., Maji, H.K., Pandey, O., Prabhakaran, M.: A rate-optimizing compiler for non-malleable codes against bit-wise tampering and permutations. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 375–397. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_16
Ball, M., Dachman-Soled, D., Kulkarni, M., Malkin, T.: Non-malleable codes for bounded depth, bounded fan-in circuits. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 881–908. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_31
Ballard, L., Green, M., de Medeiros, B., Monrose, F.: Correlation-resistant storage via keyword-searchable encryption. Cryptology ePrint Archive, Report 2005/417 (2005). http://ia.cr/2005/417
Bellare, M., Cash, D., Miller, R.: Cryptography secure against related-key attacks and tampering. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 486–503. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25385-0_26
Bellare, M., Kohno, T.: A theoretical treatment of related-key attacks: RKA-PRPs, RKA-PRFs, and applications. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 491–506. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_31
Bellare, M., Paterson, K.G., Thomson, S.: RKA security beyond the linear barrier: IBE, encryption and signatures. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 331–348. Springer, Heidelberg (2012). doi:10.1007/978-3-642-34961-4_21
Boldyreva, A., Cash, D., Fischlin, M., Warinschi, B.: Foundations of non-malleable hash and one-way functions. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 524–541. Springer, Heidelberg (2009). doi:10.1007/978-3-642-10366-7_31
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_3
Chase, M., Kohlweiss, M., Lysyanskaya, A., Meiklejohn, S.: Malleable proof systems and applications. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 281–300. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_18
Chase, M., Kohlweiss, M., Lysyanskaya, A., Meiklejohn, S.: Malleable proof systems and applications. IACR Cryptology ePrint Archive, 2012:12 (2012)
Chattopadhyay, E., Zuckerman, D.: Non-malleable codes against constant split-state tampering. In: Proceedings of the FOCS, pp. 306–315 (2014)
Chen, Y., Qin, B., Zhang, J., Deng, Y., Chow, S.S.M.: Non-malleable functions and their applications. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9615, pp. 386–416. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49387-8_15
Dachman-Soled, D., Kalai, Y.T.: Securing circuits and protocols against 1/poly(k) tampering rate. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 540–565. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_23
Dachman-Soled, D., Liu, F.-H., Shi, E., Zhou, H.-S.: Locally decodable and updatable non-malleable codes and their applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 427–450. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_18
Damgård, I., Faust, S., Mukherjee, P., Venturi, D.: Bounded tamper resilience: how to go beyond the algebraic barrier. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 140–160. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42045-0_8
Damgård, I., Faust, S., Mukherjee, P., Venturi, D.: The chaining lemma and its application. In: Lehmann, A., Wolf, S. (eds.) ICITS 2015. LNCS, vol. 9063, pp. 181–196. Springer, Heidelberg (2015). doi:10.1007/978-3-319-17470-9_11
Dodis, Y., Lewko, A.B., Waters, B., Wichs, D.: Storing secrets on continually leaky devices. In: Proceedings of the FOCS, pp. 688–697 (2011)
Dziembowski, S., Kazana, T., Obremski, M.: Non-malleable codes from two-source extractors. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 239–257. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_14
Dziembowski, S., Kazana, T., Wichs, D.: One-time computable self-erasing functions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 125–143. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_9
Dziembowski, S., Pietrzak, K.: Leakage-resilient cryptography. In: Proceedings of the FOCS, pp. 293–302 (2008)
Dziembowski, S., Pietrzak, K., Wichs, D.: Non-malleable codes. In: Innovations in Computer Science, pp. 434–452 (2010)
Faonio, A., Nielsen, J.B.: Non-malleable codes with split-state refresh. Cryptology ePrint Archive, Report 2016/1192 (2016). http://eprint.iacr.org/2016/1192
Faonio, A., Venturi, D.: Efficient public-key cryptography with bounded leakage and tamper resilience. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 877–907. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53887-6_32
Faust, S., Mukherjee, P., Nielsen, J.B., Venturi, D.: Continuous non-malleable codes. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 465–488. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_20
Faust, S., Mukherjee, P., Venturi, D., Wichs, D.: Efficient non-malleable codes and key-derivation for poly-size tampering circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 111–128. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_7
Faust, S., Pietrzak, K., Venturi, D.: Tamper-proof circuits: how to trade leakage for tamper-resilience. In: Aceto, L., Henzinger, M., Sgall, J. (eds.) ICALP 2011. LNCS, vol. 6755, pp. 391–402. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22006-7_33
Goldenberg, D., Liskov, M.: On related-secret pseudorandomness. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 255–272. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11799-2_16
Goyal, V., O’Neill, A., Rao, V.: Correlated-input secure hash functions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 182–200. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_12
Groth, J., Sahai, A.: Efficient noninteractive proof systems for bilinear groups. SIAM J. Comput. 41(5), 1193–1232 (2012)
Ishai, Y., Prabhakaran, M., Sahai, A., Wagner, D.: Private circuits II: keeping secrets in tamperable circuits. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 308–327. Springer, Heidelberg (2006). doi:10.1007/11761679_19
Jafargholi, Z., Wichs, D.: Tamper detection and continuous non-malleable codes. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 451–480. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_19
Kiayias, A., Tselekounis, Y.: Tamper resilient circuits: the adversary at the gates. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 161–180. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42045-0_9
Liu, F.-H., Lysyanskaya, A.: Tamper and leakage resilience in the split-state model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 517–532. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_30
Lu, X., Li, B., Jia, D.: Related-key security for hybrid encryption. In: Chow, S.S.M., Camenisch, J., Hui, L.C.K., Yiu, S.M. (eds.) ISC 2014. LNCS, vol. 8783, pp. 19–32. Springer, Cham (2014). doi:10.1007/978-3-319-13257-0_2
Lucks, S.: Ciphers secure against related-key attacks. In: Roy, B., Meier, W. (eds.) FSE 2004. LNCS, vol. 3017, pp. 359–370. Springer, Heidelberg (2004). doi:10.1007/978-3-540-25937-4_23
Naor, M., Segev, G.: Public-key cryptosystems resilient to key leakage. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 18–35. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_2
Qin, B., Liu, S., Yuen, T.H., Deng, R.H., Chen, K.: Continuous non-malleable key derivation and its application to related-key security. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 557–578. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_25
Wee, H.: Public key encryption against related key attacks. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 262–279. Springer, Heidelberg (2012). doi:10.1007/978-3-642-30057-8_16
Acknowledgement
The authors acknowledge support by European Research Council Starting Grant 279447. The authors acknowledge support from the Danish National Research Foundation and The National Science Foundation of China (under the grant 61361136003) for the Sino-Danish Center for the Theory of Interactive Computation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Faonio, A., Nielsen, J.B. (2017). Non-malleable Codes with Split-State Refresh. In: Fehr, S. (eds) Public-Key Cryptography – PKC 2017. PKC 2017. Lecture Notes in Computer Science(), vol 10174. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54365-8_12
Download citation
DOI: https://doi.org/10.1007/978-3-662-54365-8_12
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54364-1
Online ISBN: 978-3-662-54365-8
eBook Packages: Computer ScienceComputer Science (R0)








 Sample
Sample  Parse
Parse  Parse
Parse 
 , compute
, compute 
 , defines the transformation
, defines the transformation  , defines the transformation
, defines the transformation 
 and run the adversary
and run the adversary  and
and  and run the adversary
and run the adversary  and run the adversary
and run the adversary  and output
and output 

 and run the adversary
and run the adversary  Sample
Sample  such that
such that  Sample
Sample  ,
,  and compute
and compute  Sample
Sample  and compute
and compute  Let
Let  Parse
Parse  such that
such that  Parse
Parse  such that
such that 
 Output
Output  ;
; Output
Output  ;
; Output
Output  Output
Output