Abstract
Leakage resilient codes (LRCs) are probabilistic encoding schemes that guarantee message hiding even under some bounded leakage on the codeword. We introduce the notion of fully leakage resilient codes (FLRCs), where the adversary can leak \(\lambda _0\) bits from the encoding process, namely, the message and the randomness involved during the encoding process. In addition the adversary can as usual leak from the codeword. We give a simulation-based definition requiring that the adversary’s leakage from the encoding process and the codeword can be simulated given just \(\lambda _0\) bits of leakage from the message. We give a fairly general impossibility result for FLRCs in the popular split-state model, where the codeword is broken into independent parts and where the leakage occurs independently on the parts. We then give two feasibility results for weaker models. First, we show that for \(\mathsf {NC}^0\)-bounded leakage from the randomness and arbitrary poly-time leakage from the parts of the codeword the inner-product construction proposed by Daví et al. (SCN’10) and successively improved by Dziembowski and Faust (ASIACRYPT’11) is a FLRC for the split-state model. Second, we provide a compiler from any LRC to a FLRC in the common reference string model where the leakage on the encoding comes from a fixed leakage family of small cardinality. In particular, this compiler applies to the split-state model but also to other models.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Leakage-resilient cryptography
- Impossibility
- Fully-leakage resilience
- Simulation-based definition
- Feasibility results
1 Introduction
Leakage-resilient codes (LRCs) (also known as leakage-resilient storages) allow to store safely a secret information in a physical memory that may leak some side-channel information. Since their introduction (see Davì et al. [12]) they have found many applications either by their own or as building blocks for other leakage and tamper resilient primitives. To mention some, Dziembowski and Faust [15] proposed an efficient and continuous leakage-resilient identification scheme and a continuous leakage-resilient CCA2 cryptosystem, while Andrychowicz et al. [5] proposed a practical leakage-resilient LPN-based version of the Lapin protocol (see Heyse et al. [28]) both relying on LRCs based on the inner-product extractor. LRC found many applications also in the context of non-malleable codes (see Dziembowski et al. [17]), which, roughly speaking, can be seen as their tamper-resilience counterpart. Faust et al. [23] showed a non-malleable code based on LRC, Aggarwal et al. [1] proposed a construction of leakage and tamper resilient code and Faust et al. [21] showed continuous non-malleable codes based on LRC [21] (see also Jafargholi and Wichs [29]).
The security requirement of LRC states that given two encoded messages, arbitrarily but bounded length leakage on the codeword is indistinguishable. Ideally, a good LRC should be resilient to a leakage that can be much longer than the size of the message protected, however, to get such strong guarantee some restriction on the class of leakage allowed must be set. Intuitively, any scheme where the adversary can even partially compute the decoding function as leakage cannot be secure. A way to fix this problem is to consider randomly chosen LRCs. As showed in [12], and successively improved in [23, 29], for any fixed set of leakage functions, there exists a family of efficiently computable codes such that with high probability a code from this family is leakage resilient. From a cryptographic perspective, the results known in this direction can be interpreted as being in the “common reference string” model, where the leakage class is set and, then, the LRC is sampled.
Another way, more relevant for our paper, is to consider the split-state model [16, 27] where the message is encoded in two (or more) codewords and the leakage happens adaptively but independently from each codeword, thus the decoding function cannot automatically be part of the allowed leakage, which opens the possibility of constructing a LRC.
It is easy to see that the encoding algorithm must be randomized, otherwise two fixed messages can be easily distinguished. However, the security of LRC does not give any guarantee when there is leakage from the randomness used in the encoding process. In other words, while the encoded message can be stored in a leaky device the encoding process must be executed in a completely leak-free environment. A stronger flavour of security where we allow leakage from the encoding process is usually called fully leakage resilient.
Our Contributions. We generalize the notion of LRC to the setting of fully leakage resilience. Roughly speaking, a fully leakage-resilient code (FLRC) hides information about the secret message even when the adversary leaked information during the encoding process. Our contributions are summarized as follow:
-
1.
We provide a simulation-based definition of fully leakage-resilient codes. The definition postulates that for any adversary leaking \(\lambda _0\) bits from the encoding process and \(\lambda _1\) bits from the codewords there exists a simulator which provides a view that is indistinguishable. Our definition is, in some sense, the minimal one suitable for the fully leakage resilience setting. As a sanity check, we show that our new notion is implied by the indistinguishability-based definition of [12] for \(\lambda _0 = 0\).
-
2.
We show that there does not exist an efficient coding scheme in the split-state model that is a fully leakage resilient code if the leakage function is allowed to be any poly-time function. Our result holds for coding schemes where the length of the messages is at least linear in the security parameter and under the sole assumption that collision-resistant hash functions exist. We can generalize the impossibility result to the case of constant-length messages under the much stronger assumption that differing-input obfuscation (diO) exists (see [3, 9]).
-
3.
We provide two feasibility results for weaker models. We show that, if the leakage from the randomness is computable by bounded-depth constant fan-in circuits (i.e. \(\mathsf {NC}^0\)-computable leakage), the inner-product extractor LRC of [12] is fully leakage resilient. We show a compiler from any LRC to a fully leakage resilient code in the common reference string model for any fixed leakage-from-the-encoding-process family of small cardinality.
Simulation-Based Security. Consider the naive fully leakage-resilient extension of the indistinguishability-based security definition of LRC. Roughly speaking, the adversary plays against a challenger and it can leak \(\lambda _0>0\) bits from a random string  , in a second phase, the adversary sends to the challenger two messages \(m_0,m_1\), the challenger chooses a random bit b and encodes the message \(m_b\) using the randomness \(\omega \). After this, the adversary gets access to leakage from the codewords. We show an easy attack on this definition. The attacker can compute, via one leakage function on the randomness, the encoding of both \(m_0\) and \(m_1\) and find a coordinate in which the two codewords differ, successively, by leaking from the codeword only one bit, it can check whether \(m_0\) or \(m_1\) has been encoded.
, in a second phase, the adversary sends to the challenger two messages \(m_0,m_1\), the challenger chooses a random bit b and encodes the message \(m_b\) using the randomness \(\omega \). After this, the adversary gets access to leakage from the codewords. We show an easy attack on this definition. The attacker can compute, via one leakage function on the randomness, the encoding of both \(m_0\) and \(m_1\) and find a coordinate in which the two codewords differ, successively, by leaking from the codeword only one bit, it can check whether \(m_0\) or \(m_1\) has been encoded.
The problem with the indistinguishability-based security definition sketched above is that it concentrates on preserving, in the presence of leakage on the randomness, the same security guarantees as the (standard) leakage resilient definition. However, the ability of leaking before and after the challenge generation, as shown for many other cryptographic primitives, gives to the adversary too much power.
Following the leakage-tolerant paradigm introduced by Bitansky et al. [7], we instead consider a simulation-based notion of security. The definition postulates that for any adversary leaking \(\lambda _0\) bits from the encoding process and \(\lambda _1\) bits from the codeword there exists a simulator which provide a view that is indistinguishable. In particular, the adversary chooses one input message and forwards it to the challenger of the security game. After that, the adversary can leak first from the encoding process and then from the codeword. The job of the simulator is to produce an indistinguishable view of the leakage oracles to the adversary given only leakage oracle access to the message. It is not hard to see that, without the help of leakage oracle on the message, the task would be impossible. In fact, the adversary can leak bits of the input message, if the input message is randomly chosen the simulator cannot provide an indistinguishable view. Therefore, the simulator can leak up to \(\lambda _0(1+\gamma )\) bits from the message for a “slack parameter” \(\gamma \geqslant 0\). The idea is that some information about the message can unavoidably leak from the encoding process, however the amount of information about the message that the adversary gathers by jointly leaking from the encoding process and from the codeword should not exceed by too much the the bound given by the leakage on the encoding process. The slack parameter is often considered as a reasonable weakening of the model in the context of fully leakage resilience (see for example [19, 26, 27, 39]), we include it in our model to make the impossibility results stronger. For the feasibility results we will instead ignore it.
The Impossibility Results. We give an impossibility result for FLRCs in the split-state model. Recall that, in the split state model, the codeword is divided in two parts which are stored in two independent leaky devices. Each leakage query can be any poly-time function of the data stored in one of the parts.
Here we give the intuition behind the attacker. For simplicity let us set the slack parameter \(\gamma \) equal to 0. In our attack we leak from the encoding process a hash of each of the two parts of the codeword. The leakage function takes the message and the randomness, runs the encoding algorithm to compute the two parts L and R (the left part and the right part) and leaks two hash values \(h_l = h(L)\) and \(h_r = h(R)\). Then we use a succinct argument of knowledge system to leak an argument of knowledge of pre-images L and R of \(h_l\) and \(h_r\) for which it holds that (L, R) decodes to m. Let \(\lambda _0\) be equal to the length of the two hashed values and the transcript of the succinct argument. After this the message can be encoded. The adversary uses its oracle access to L to leak, in sequence, several succinct arguments of knowledge of L such that \(h_l = h(L)\). Similarly, the adversary uses its oracle access to R to leak, in sequence, several succinct arguments of knowledge of R such that \(h_r = h(R)\). By setting \(\lambda _1\gg \lambda _0\) we can within the leakage bound \(\lambda _1\) on L and R leak \(17 \lambda _0\) succinct arguments of knowledge of L and R. Suppose that the code is secure, then there exists a simulator which can simulate the leakage of \(h_l\) and \(h_r\) and all the arguments given at most \(\lambda _0\) bits of leakage on m. Since the arguments are accepting in the real world and the simulator is assumed to be good it follows that the simulated arguments are accepting with probability close to 1. Since the simulator has access to only \(\lambda _0\) bits of leakage on m it follows that for one of the \(17 \lambda _0\) simulated arguments produced by the simulator it uses the leakage oracle on m with probability at most \(\frac{1}{4}\). This means that with probability \(\frac{3}{4}\) the simulator is not even using the leakage oracle to simulate this argument, so if we remove the access to leakage from m the argument will still be acceptable with probability close to \(\frac{3}{4}\). Hence if the argument systems has knowledge error just \(\frac{1}{2}\) we can extract L from this argument with probability close to \(\frac{1}{4}\). Similarly we can extract from one of the arguments of knowledge of R the value R with probability close to \(\frac{1}{4}\). By collision resistance and soundness of the first argument leaked from the encoding process it follows that (L, R) decodes to m. This means that we can extract from the simulator the message m with probability negligibly close to \(\frac{1}{16}\) while using only \(\lambda _0\) bits of leakage on m. If m is uniformly random and just \(\lambda _0+6\) bits long, this is a contradiction. In fact, the amount of min-entropy of m after have leaked \(\lambda _0\) bits is \(\lambda _0+6-\lambda _0= 6\), therefore m cannot be guessed with probability better than \(2^{-6}\).
Similar proof techniques have been used already by Nielsen et al. [38] to prove a connection between leakage resilience and adaptive security and recently by Ostrovsky et al. [40] to prove an impossibility result for certain flavors of leakage-resilient zero-knowledge proof systems. The way we apply this type of argument here is novel. It is in particular a new idea to use many arguments of knowledge in sequence to sufficient restrict the simulators ability to leak from its leakage oracle in one of the proofs.
The definition of FLR makes sense only when the leakage parameter \(\lambda _0\) is strictly smaller than the size of the message. The proposed attack needs to leak at least a collision resistant hash function of the codeword, therefore the length of the message needs to be super-logarithmic in the security parameter. Thus the technique cannot be used to give an impossibility result for FLRC with message space of constant length. We can overcome this problem relying on the concept of Predictable ZAP (PZAP) recently proposed by Faonio et al. [20]. A PZAP is an extremely succinct 2-message argument of knowledge where the prover can first see the challenge from the verifier and then decide the instance. This allows the attacker to implement the first check by just leaking a constant-length argument that the hashed values of the two parts of the codeword are well formed (without actually leaking the hashed values) and then, successively, leak the hashed values from the codeword and check the validity of the argument. PZAP are shown to imply extractable witness encryption (see Boyle et al. [9]) and therefore the “implausibility” result of Garg et al. [25] applies. We interpret our second impossibility result as an evidence that constant-length FLRC are hard to construct as such a code would not only make extractable witness encryption implausible, but it would prove it impossible under the only assumption that collision-resistant hash functions exists. We provide more details in the full version of the paper [18].
The Feasibility Results. The ability to leak a collision resistant hash function of the randomness is necessary for the impossibility result. Therefore, the natural question is: If we restrict the leakage class so that collision resistant hash functions cannot be computed as leakage on the randomness, can we find a coding scheme that is fully leakage resilient? We answer this question affirmatively.
We consider the class \(\mathsf {NC}^0\) of constant-depth constant fan-in circuits and we show that the LRC based on the inner-product extractor (and more general LRCs where there is an \(\mathsf {NC}^0\) function that maps the randomness to the codeword) are fully leakage resilient. The intuition is that \(\mathsf {NC}^0\) leakage is not powerful enough to break all the “independence” between the two parts of the codeword. Technically, we are able to cast every leakage query on the randomness into two slightly bigger and independent leakage queries on the two parts of the codeword. Notice that collision resistant hash functions cannot be computed by \(\mathsf {NC}^0\) circuits. This is necessary. In fact, proving a similar result for a bigger complexity class automatically implies a lower bound on the complexity of computing either collision resistant hash functions or arguments of knowledge. Intuitively, this provides a strong evidence that is hard to construct FLRC even for bounded classes of leakage.
Another important property that we exploit in the impossibility result is that, given access to the leakage oracle on the randomness, we can compute the codeword. A second path to avoid the impossibility results is to consider weaker models of security where this is not permitted. We point out that the schemes proposed by [12, 23, 29] in the common reference string model can be easily proved to be fully leakage resilient. Inspired by the above results we provide a compiler that maps any LRC to FLRC for any fixed leakage-from-the-encoding family \(\mathcal {F} \) of small cardinality. Notice that the bound is on the cardinality of the leakage class and not on its complexity (in principle, the leakage class could contain collision resistant hash functions).
We remark that the definition of FLRC already assumes a CRS (this to include in our model the result of Liu and Lysyanskaya [34]). The key point is that, by fixing \(\mathcal {F} \) ahead (namely, before the common reference string is sampled) and because of the small cardinality, the adversary cannot make the leakage on the encoding “depends” from the common reference string, disabling therefore the computation of the encoded word as leakage on the encoding process.
Technically, we use a result of Trevisan and Vadhan [43] which proves that for any fixed leakage class \(\mathcal {F} \) a t-wise independent hash function (the parameter t depends on the cardinality of \(\mathcal {F} \)) is a deterministic extractor with high probability. The proof mostly follows the template given in [23].
Related Work. Cryptographic schemes are designed under the assumption that the adversary cannot learn any information about the secret key. However, side-channel attacks (see [32, 33, 42]) have showed that this assumption does not always hold. These attacks have motivated the design of leakage-resilient cryptosystems which remain secure even against adversaries that may obtain partial information about the secret state. Starting from the groundbreaking result of Micali and Reyzin [36], successively either gradually stronger or different models have been considered (see for example [2, 16, 24, 37]). Fully leakage resilient schemes are known for signatures [11, 19, 35], zero-knowledge proof system [4, 26, 41] and multi-party computation protocols [8, 10]. Similar concepts of leakage resilient codes have been considered, Liu and Lysyanskaya [34] and successively Aggarwal et al. [1] constructed leakage and tamper resilient codes while Dodis et al. [13] constructed continual leakage resilient storage. Simulation-based definitions in the context of leakage-resilient cryptography were also adopted in the case of zero-knowledge proof (see [4, 26, 41]), public-key encryption (see [27]) and signature schemes (see [39]). As mentioned already, our proof technique for the impossibility result is inspired by the works of Nielsen et al. [38] and Ostrovsky et al. [40], however, part of the analysis diverges, and instead resembles an information theoretic argument already known in leakage-resilient cryptography (see for example [2, 19, 30]).
In [22] the authors present a RAM model of computation where a CPU is connected to some constant number of memories, paralleling the split-state model that we use here. The memories and buses are assumed to be leaky, but the CPU is assumed to be leakage free. Besides leakage, the paper also shows how to handle tampering, like moving around codewords in the memories. They show how to use a leakage-resilient and tamper-resilient code to securely compute on this platform. In each step the CPU will read from the disks a number of codewords, decode these, do a computation on the plaintext, re-encode the results and write the codewords back in the memories. One should wonder if it is possible to get a similar result for the more realistic model where there is a little leakage from the CPU? It is clear that if the CPU can leak, then it can also leak from the plaintexts it is working on. This can be handled by having the computation that is done on the plaintexts being leakage resilient in itself. The challenging part is then to show that the leakage from the CPU during re-encoding of the results to be stored in the memories can be simulated given just a little leakage on the results themeselves. This would in particular require that the code is fully leakage-resilient in the sense we define in this paper. Our negative results therefore do not bode well for this proof strategy. On the other hand, our positive results open up the possibility of tolerating some simple leakage from the CPU or getting a result for weaker models, like the random oracle model. Note, however, that the code would have to be tamper-resilient in addition to being fully leakage resilient, so there still seem to be significant obstacles towards proving such a result.
Roadmap. In Sect. 2 we introduce the necessary notation for probability and cryptographic tools. In Sect. 3 we provide the simulation-based definition for Fully Leakage-Resilient Codes. In Sect. 4 we state and prove the main impossibility result for linear-size message spaces. In Sect. 5 we provide the two feasibility results, specifically, in Sect. 5.1 we give a FLR code for the class \(\mathsf {NC}^0\) and in Sect. 5.2 we give a compiler from Leakage-Resilient Codes to Fully Leakage-Resilient Codes for any fixed class of small cardinality.
2 Preliminaries
We let \(\mathbb {N}\) denote the naturals and \(\mathbb {R}\) denote the reals. For \(a,b \in \mathbb {R}\), we let \([a,b]=\{x\in \mathbb {R}\ :\ a\le x\le b\}\); for \(a\in \mathbb {N}\) we let \([a] = \{1,2,\ldots ,a\}\). If x is a string, we denote its length by |x|; if \(\mathcal {X}\) is a set, \(|\mathcal {X}|\) represents the number of elements in \(\mathcal {X}\). When x is chosen randomly in \(\mathcal {X}\), we write  . When \(\mathcal {A} \) is an algorithm, we write \(y \leftarrow \mathcal {A} (x)\) to denote a run of \(\mathcal {A} \) on input x and output y; if \(\mathcal {A} \) is randomized, then y is a random variable and \(\mathcal {A} (x;r)\) denotes a run of \(\mathcal {A} \) on input x and randomness r. An algorithm \(\mathcal {A} \) is probabilistic polynomial-time (\(\mathsf {ppt}\)) if \(\mathcal {A} \) is allowed to use random choices and for any input \(x\in \{0,1\}^*\) and randomness \(r \in \{0,1\}^*\) the computation of \(\mathcal {A} (x;r)\) terminates in at most \(\mathsf {poly} (|x|)\) steps.
. When \(\mathcal {A} \) is an algorithm, we write \(y \leftarrow \mathcal {A} (x)\) to denote a run of \(\mathcal {A} \) on input x and output y; if \(\mathcal {A} \) is randomized, then y is a random variable and \(\mathcal {A} (x;r)\) denotes a run of \(\mathcal {A} \) on input x and randomness r. An algorithm \(\mathcal {A} \) is probabilistic polynomial-time (\(\mathsf {ppt}\)) if \(\mathcal {A} \) is allowed to use random choices and for any input \(x\in \{0,1\}^*\) and randomness \(r \in \{0,1\}^*\) the computation of \(\mathcal {A} (x;r)\) terminates in at most \(\mathsf {poly} (|x|)\) steps.
Let \(\kappa \) be a security parameter. A function \(\mathsf {negl} \) is called negligible in \(\kappa \) (or simply negligible) if it vanishes faster than the inverse of any polynomial in \(\kappa \). For a relation \(\mathcal {R}\subseteq \{0,1\}^{*}\times \{0,1\}^{*}\), the language associated with \(\mathcal {R}\) is \(\mathcal {L}_\mathcal {R}= \{x:\exists w\text { s.t. }(x,w)\in \mathcal {R}\}\).
For two ensembles \(\mathcal {X}=\{X_\kappa \}_{\kappa \in \mathbb N}\), \(\mathcal {Y}=\{Y_\kappa \}_{\kappa \in \mathbb N}\), we write \(\mathcal X \mathop {\mathop {\approx }\limits ^{c}}\nolimits _{\epsilon } \mathcal Y\), meaning that every probabilistic polynomial-time distinguisher D has \(\epsilon (\kappa )\) advantage in distinguishing \(\mathcal X\) and \(\mathcal Y\), i.e., \(\frac{1}{2} \vert \Pr [D(\mathcal X_\kappa )=1] - \Pr [D(\mathcal Y_\kappa )=1] \vert \le \epsilon (\kappa )\) for all sufficiently large values of \(\kappa \).
We simply write \(\mathcal X \mathop {\approx }\limits ^{c}\mathcal Y\) when there exists a negligible function \(\epsilon \) such that \(\mathcal {X} \mathop {\mathop {\approx }\limits ^{c}}\nolimits _\epsilon \mathcal {Y} \). Similarly, we write \(\mathcal X \approx _\epsilon \mathcal Y\) (statistical indistinguishability), meaning that every unbounded distinguisher has \(\epsilon (\kappa )\) advantage in distinguishing \(\mathcal {X} \) and \(\mathcal {Y} \). Given two ensembles \(\mathcal {X} \) and \(\mathcal {Y} \) such that \(\mathcal {X} \approx _\epsilon \mathcal {Y} \) the following holds:
We recall the notion of (average) conditional min-entropy. We adopt the definition given in [2], where the authors generalize the notion of conditional min-entropy to interactive predictors that participate in some randomized experiment \(\mathbf {E} \). The conditional min-entropy of random variable X given any randomized experiment \(\mathbf {E} \) is defined as \( \widetilde{\mathbb {H}}_\infty \left( X \left| \right. \mathbf {E} \right) = \max _{\mathcal {B}}\left( - \log \Pr [ \mathcal {B} ()^{\mathbf {E}}=X] \right) \), where the maximum is taken over all predictors without any requirement on efficiency. Note that w.l.o.g. the predictor \(\mathcal {B} \) is deterministic, in fact, we can de-randomize \(\mathcal {B} \) by hardwiring the random coins that maximize its outcome. Sometimes we write \(\widetilde{\mathbb {H}}_\infty ( X | Y )\) for a random variable Y, in this case we mean the average conditional min-entropy of X given the random experiment that gives Y as input to the predictor. Given a string \(X\in \{0,1\}^*\) and a value \(\lambda \in \mathbb {N}\) let the oracle \(\mathcal {O} _\lambda ^X(\cdot )\) be the leakage oracle that accepts as input functions \(f_1,f_2,\dots \) defined as circuits and outputs \(f_1(X),f_2(X),\dots \) under the restriction that \(\sum _i |f_i(X)| \leqslant \lambda \).
We recall here a lemma of Alwen et al. [2] and a lemma from Bellare and Rompel [6] that we make us of.
Lemma 1
For any random variable X and for any experiment \(\mathbf {E} \) with oracle access to \(\mathcal {O} _\lambda ^X(\cdot )\), consider the experiment \(\mathbf {E} '\) which is the same as \(\mathbf {E} \) except that the predictor does not have oracle access to \(\mathcal {O} _\lambda ^X(\cdot )\). Then \(\widetilde{\mathbb {H}}_\infty \left( X \left| \right. \mathbf {E} \right) \geqslant \widetilde{\mathbb {H}}_\infty \left( X \left| \right. \mathbf {E} ' \right) - \lambda \).
Lemma 2
Let \(t \geqslant 4\) be an even integer. Suppose \(X_1,\dots ,X_n\) are t-wise independent random variables taking values in [0, 1]. Let \(X := \sum _i X_i\) and define \(\mu := {{\mathrm{\mathbb {E}}}}[X]\) to be the expectation of the sum. Then, for any \(A > 0\), \(\Pr [|X - \mu | \geqslant A] \leqslant 8\left( \tfrac{t\mu +t^2}{A^2}\right) ^{t/2}\).
2.1 Cryptographic Primitives
Arguments of Knowledge. Our results are based on the existence of round-efficient interactive argument systems. We follow some of the notation of Wee [44]. The knowledge soundness definition is taken from [40]. A public-coin argument system (P(w), V)(x) with round complexity \(\rho (\kappa )\) is fully described by the tuple of \(\mathsf {ppt}\) algorithms \((\mathsf {Prove},\mathsf {Judge})\) where:
-
V on input x samples uniformly random strings
 , P on inputs x, w samples uniformly random string
, P on inputs x, w samples uniformly random string 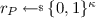 .
. -
For any \(i\in [\rho (\kappa )]\), V sends the message \(y_i\) and P replies with the message \(x_i:=\mathsf {Prove} (x,w,{y}_{1},\ldots ,{y}_{i};r_P)\).
-
The verifier V executes \(j:=\mathsf {Judge}\big (x,{y}_{1},\ldots ,{y}_{\rho (\kappa )},{x}_{1},\ldots ,{x}_{\rho (\kappa )}\big )\) and accepts if \(j=1\).
Definition 1
(Argument of knowledge). An interactive protocol (P, V) is an argument of knowledge for a language \(\mathcal {L}\) if there is a relation \(\mathcal {R}\) such that \(\mathcal {L}= \mathcal {L}_\mathcal {R}:= \{ x \vert \exists w : (x,w) \in \mathcal {R}\}\), and functions \(\nu ,s:\mathbb {N}\rightarrow [0,1]\) such that \(1-\nu (\kappa ) > s(\kappa ) + 1/\mathsf {poly} (\kappa )\) and the following conditions hold.
-
(Efficiency): The length of all the exchanged messages is polynomially bounded, and both P and V are computable in probabilistic polynomial time;
-
(Completeness): If \((x,w)\in \mathcal {R}\), then V accepts in (P(w), V)(x) with probability at least \(1-\nu (|x|)\).
-
(Knowledge Soundness): For every \(\mathsf {ppt}\) prover strategy \(P^*\), there exists an expected polynomial-time algorithm \(\mathsf {K}\) (called the knowledge extractor) such that for every \(x,z,r\in \{0,1\}^*\) if we denote by \(p^*(x,z,r)\) the probability that V accepts in (P(z; r), V)(x), then \(p^*(x,z,r) > s(|x|)\) implies that
$$ \Pr [\mathsf {K}(P^*,x,z,r)\in \mathcal {R}(x)]\geqslant p^*(x,z,r) - s(|x|). $$
The value \(\nu (\cdot )\) is called the completeness error and the value \(s(\cdot )\) is called the knowledge error. We say (P, V) has perfect completeness if \(\nu = 0\). The communication complexity of the argument system is the total length of all messages exchanged during an execution; the round complexity is the total number of exchanged messages. We write \(\mathsf {AoK}_{\nu ,s}(\rho (\kappa ),\lambda (\kappa ))\) to denote interactive argument on knowledge systems with completeness error \(\nu \), knowledge error \(s\), round-complexity \(\rho (\kappa )\) and communication complexity \(\lambda (\kappa )\). Sometimes we also write \(\lambda (\kappa ) = \lambda _P(\kappa )+\lambda _V(\kappa )\) to differentiate between the communication complexity of the prover and of the verifier. We say (P, V) is succinct if \(\lambda (\kappa )\) is poly-logarithmic in the length of the witness and the statement being proven.
We remark that for our results interactive arguments are sufficient; in particular our theorems can be based on the assumption that collision-resistant function ensembles exist [31].
Collision Resistant Hash Functions. Let \(({\mathsf {Gen}}^{\texttt {CRH}},\mathsf {Eval}^{{\texttt {CRH}}})\) be a tuple of \(\mathsf {ppt}\) algorithms such that upon input \(1^\kappa \) the algorithm \({\mathsf {Gen}}\) outputs an evaluation key h and upon inputs h and a string \(x\in \{0,1\}^*\) the deterministic algorithm \(\mathsf {Eval}^{{\texttt {CRH}}}\) outputs a string \(y\in \{0,1\}^{\ell _{\mathsf {CRH}}(\kappa )}\). We shorten the notation by writing h(x) for \(\mathsf {Eval}^{{\texttt {CRH}}}(h,x)\).
Definition 2
A tuple  is a collision-resistant hash function (family) with output length \(\ell _\mathsf {CRH}(\kappa )\) if for all non-uniform polynomial time adversary \(\mathcal {B} _{coll}\) there exists a negligible function \(\mathsf {negl} \) such that the following holds:
is a collision-resistant hash function (family) with output length \(\ell _\mathsf {CRH}(\kappa )\) if for all non-uniform polynomial time adversary \(\mathcal {B} _{coll}\) there exists a negligible function \(\mathsf {negl} \) such that the following holds:

For simplicity we consider the model of non-uniform polynomial time adversaries. Note, however, that our results hold also if we consider the model \(\mathsf {ppt}\) adversaries.
3 Definition
In this section we give the definition of Fully Leakage Resilient Codes. The definition given is specialized for the 2-split-state model, we adopt this definition instead of a more general one for simplicity. The results given in Sect. 4 can be adapted to hold for the more general k-split model (see Remark 1). LRCs of [12, 21, 29] in the common reference string model can be proved fully-leakage resilience (see Sect. 5). Therefore the syntax given allows the scheme to depends on a common reference string to include the scheme of [34].
An \((\alpha ,\beta )\)-split-coding scheme is a tuple \(\varSigma =({\mathsf {Gen}},\mathsf {Enc},{\mathsf {Dec}})\) of \(\mathsf {ppt} \) algorithms with the following syntax:
-
\({\mathsf {Gen}}\) on input \(1^\kappa \) outputs a common reference string \(\mathsf {crs}\);
-
\(\mathsf {Enc} \) on inputs \(\mathsf {crs}\) and a message \(m\in \mathcal {M} _\kappa \) outputs a tuple \((L,R)\in \mathcal {C} _\kappa \times \mathcal {C} _\kappa \);
-
\({\mathsf {Dec}}\) is a deterministic algorithm that on inputs \(\mathsf {crs}\) and a codeword \((L,R)\in \mathcal {C} _\kappa \times \mathcal {C} _\kappa \) decodes to \(m'\in \mathcal {M} _\kappa \).
Here \(\mathcal {M} _\kappa = \{0,1\}^{\alpha (\kappa )}\), \(\mathcal {C} _\kappa = \{0,1\}^{\beta (\kappa )}\) and the randomness space of \(\mathsf {Enc} \) is \(\mathcal {R} _k = \{0,1\}^{p(\kappa )}\) for a fixed polynomial p.
A split-coding scheme is correct if for any \(\kappa \) and any \(m\in \mathcal {M} _\kappa \) we have \(\Pr _{\mathsf {crs},r_e}[{\mathsf {Dec}}(\mathsf {crs},\mathsf {Enc} (\mathsf {crs},m;r_e))=m]=1\). In what follows, whenever it is clear from the context, we will omit the security parameter \(\kappa \) so we will write \(\alpha ,\beta \) instead of \(\alpha (\kappa ),\beta (\kappa )\), etc.
Given an \((\alpha ,\beta )\)-split-coding scheme \(\varSigma \), for any \(\mathcal {A} =(\mathcal {A} _0,\mathcal {A} _1)\) and any function \(\lambda _0,\lambda _1\) let \({\mathsf {Real}}_{\mathcal {A},\varSigma }^{\lambda _0,\lambda _1}(\kappa )\) be the following experiment:
Sampling Phase. The experiment runs the adversary \(\mathcal {A} _0\) on input  and randomness
and randomness  for a polynomial p that bounds the running time of \(\mathcal {A} _0\). The adversary outputs a message \(m\in \mathcal {M} _\kappa \) and a state value st. The experiment samples
for a polynomial p that bounds the running time of \(\mathcal {A} _0\). The adversary outputs a message \(m\in \mathcal {M} _\kappa \) and a state value st. The experiment samples  and instantiates a leakage oracle \(\mathcal {O} _{\lambda _0}^{\omega \Vert m} \).
and instantiates a leakage oracle \(\mathcal {O} _{\lambda _0}^{\omega \Vert m} \).
Encoding Phase. The experiment runs the adversary \(\mathcal {A} _1\) on input st and \(\mathsf {crs}\). Moreover, the experiment sets an index \(i:=0\).
-
Upon query \((\mathtt {rand},f)\) from the adversary where f is the description of a function with domain \(\mathcal {R} _\kappa \times \mathcal {M} _\kappa \), the experiment sets \(i:=i+1\), computes \(\mathsf {lk}_{\omega }^{i}:=\mathcal {O} _{\lambda _0}^{\omega \Vert m} (f)\) and returns the value to the adversary.
-
Eventually, the adversary notifies the experiment by sending the message encode.
The message is encoded, namely the experiment defines \((L,R):=\mathsf {Enc} (\mathsf {crs},m;\omega )\) and instantiates the oracles \(\mathcal {O} _{\lambda _1}^L \), \(\mathcal {O} _{\lambda _1}^R \). Moreover, the experiment sets two indexes \(l:=0\) and \(r:=0\).
-
Upon query \((\mathtt {L},f)\) from the adversary where f is the description of a function with domain \(\mathcal {C} _\kappa \), the experiment sets \(l:=l+1\), computes \(\mathsf {lk}^l_{L}:=\mathcal {O} _{\lambda _1}^L (f)\) and returns the value to the adversary.
-
Upon query \((\mathtt {R},f)\) from the adversary where f is the description of a function with domain \(\mathcal {C} _\kappa \), the experiment sets \(r:=r+1\), computes \(\mathsf {lk}^r_{R}:=\mathcal {O} _{\lambda _1}^R (f)\) and returns the value to the adversary.
By overloading the notation, we let \({\mathsf {Real}}_{\mathcal {A},\varSigma }^{\lambda _0,\lambda _1}\) be also the tuple of random variables that describes the view of \(\mathcal {A} \) in the experiment:
Given an adversary \(\mathcal {A} =(\mathcal {A} _0,\mathcal {A} _1)\), a simulator \(\mathcal {S} \) and a slack parameter \(\gamma (\kappa )\) such that \(0\leqslant \gamma (\kappa )< \tfrac{\alpha (\kappa )}{\lambda _0(\kappa )} - 1\) let \(\mathsf {Ideal}^{\lambda _0,\lambda _1}_{\mathcal {A},\mathcal {S},\gamma }(\kappa )\) be the following experiment:
-
Sampling Phase. The experiment runs the adversary \(\mathcal {A} _0\) on input
 and randomness
and randomness  for a polynomial p that bounds the running time of \(\mathcal {A} _0\). The adversary outputs a message \(m\in \mathcal {M} _\kappa \) and a state value st. The experiment instantiates an oracle \(\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m \).
for a polynomial p that bounds the running time of \(\mathcal {A} _0\). The adversary outputs a message \(m\in \mathcal {M} _\kappa \) and a state value st. The experiment instantiates an oracle \(\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m \). -
Encoding Phase. The experiment runs the adversary \(\mathcal {A} _1\) on input st and \(\mathsf {crs}\), and the simulator \(\mathcal {S} \) on input \(\mathsf {crs}\).
-
Upon query (X, f) from the adversary where \(X\in \{\mathtt {rand},\mathtt {L},\mathtt {R}\}\) the experiment forwards the query to the simulator \(\mathcal {S} \) which returns an answer to the adversary.
-
Upon query \((\mathtt {msg},f)\) from the simulator the experiment computes \(\mathsf {lk}_m:=\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m (f)\) and returns an answer to the simulator.
As we did with \({\mathsf {Real}}_{\mathcal {A},\varSigma }^{\lambda _0,\lambda _1}\) we denote with \(\mathsf {Ideal}^{\lambda _0,\lambda _1}_{\mathcal {A},\mathcal {S},\gamma }\) also the tuple of random variables that describe the view of \(\mathcal {A} \) in the experiment. To mark the distinction between the real experiment and ideal experiment we upper script the “simulated” components of the ideal experiment with a tilde, namely:
Given a class of leakage functions \(\varLambda \) we say that an adversary is \(\varLambda \)-bounded if it submits only queries \((\mathtt {rand},f)\) where the function \(f\in \varLambda \).
Definition 3
(Simulation-based \(\varLambda \) -fully leakage resilient code). An \((\alpha ,\beta )\)-split-coding scheme is said to be \((\varLambda ,\lambda _0,\lambda _1,\epsilon )\)-FLR-sim-secure with slack parameter \(0\leqslant \gamma <\alpha /\lambda _0 -1\) if for any \(\mathsf {ppt} \) adversary \(\mathcal {A} \) that is \(\varLambda \)-bounded there exists a \(\mathsf {ppt} \) simulator \(\mathcal {S} \) such that \(\left\{ {\mathsf {Real}}_{\mathcal {A},\varSigma }^{\lambda _0,\lambda _1}(\kappa )\right\} _{\kappa \in \mathbb N} \mathop {\mathop {\approx }\limits ^{c}}\nolimits _\epsilon \left\{ \mathsf {Ideal}^{\lambda _0,\lambda _1}_{\mathcal {A},\mathcal {S},\gamma }(\kappa )\right\} _{\kappa \in \mathbb N}\).
Let \(\mathsf {P}_{/\mathsf {poly}}\) be the set of all polynomial-sized circuits.
Definition 4
(Simulation-based fully leakage resilient code). An \((\alpha ,\beta )\)-split-coding scheme is said to be \((\lambda _0,\lambda _1,\epsilon )\)-FLR-sim-secure with slack parameter \(\gamma \) if it is \((\mathsf {P}_{/\mathsf {poly}},\lambda _0,\lambda _1,\epsilon )\)-FLR-sim-secure with slack parameter \(\gamma \). We simply say that a split-coding scheme is \((\lambda _0,\lambda _1)\)-FLR-sim-secure if there exists a negligible function \(\mathsf {negl} \) and a constant \(\gamma <\alpha /\lambda _0 -1\) such that the scheme is \((\lambda _0,\lambda _1,\mathsf {negl})\)-FLR-sim-secure with slack parameter \(\gamma \).
In the full version of the paper [18] we prove that the game-based definition of [12] implies FLR-sim-security for \(\lambda _0=0\).
4 Impossibility Results
In this section we show the main result of this paper. Throughout the section we let the class of leakage functions be \(\varLambda = \mathsf {P}_{/\mathsf {poly}}\). We prove that \((\alpha ,\beta )\)-split-coding schemes that are \((\lambda _0,\lambda _1)\)-FLR-sim-secure don’t exist for many interesting parameters of \(\alpha ,\beta ,\lambda _0\) and \(\lambda _1\). We start with the case \(\alpha (\kappa )=\varOmega (\kappa )\), the impossibility results holds under the only assumption that collision resistant hash functions exist. For the case \(\alpha (\kappa )=O(1)\), the impossibility results holds under the stronger assumption that adaptive-secure PAoK exists.
Theorem 1
If public-coin \(\mathsf {AoK}_{\mathsf {negl} (\kappa ),1/2}(O(1),\ell _\mathsf {AoK}(\kappa ))\) for \(\mathsf {NP} \) and collision-resistant hash functions with output length \(\ell _\mathsf {CRH}(\kappa )\) exist then for any \(\lambda _0\geqslant \ell _\mathsf {AoK}(\kappa ) + 2\cdot \ell _\mathsf {CRH}(\kappa )\) for any \(\gamma \geqslant 0\) and for any \((\alpha ,\beta )\)-split-coding scheme \(\varSigma \) with \(\alpha (\kappa )\geqslant \lambda _0(\kappa )\cdot (1+\gamma )+ \ell _\mathsf {CRH}(\kappa )+7\) and if \(\lambda _1(\kappa ) \geqslant 17\lambda _0(\kappa )\cdot (1+\gamma )\cdot \ell _\mathsf {AoK}(\kappa )\) then \(\varSigma \) is not \((\lambda _0,\lambda _1)\)-FLR-sim-secure.
Proof
We first set some necessary notation. Given a random variable x we use the notation \(\bar{x}\) to refer to a possible assignment of the random variable. Let \(({\mathsf {Gen}}^{\texttt {CRH}},\mathsf {Eval}^{{\texttt {CRH}}})\) be a collision resistant hash function with output length \(\ell _\mathsf {CRH}(\kappa )\).
Leakage-Aided Prover. Let \(\varPi =(\mathsf {Prove},\mathsf {Judge})\) be in \(\mathsf {AoK}_{1/2,\mathsf {negl} (\kappa )}(O(1),\ell _\mathsf {AoK}(\kappa ))\) and a public-coin argument system for \(\mathsf {NP} \). For concreteness let \(\rho \) be the round complexity of the \(\varPi \). We say that an attacker leaks an argument of knowledge for \(x\in \mathcal {L}_\mathcal {R}\) from \(\mathtt {X}\in \{\mathtt {rand}, \mathtt {L}, \mathtt {R} \}\) if the attacker proceeds with the following sequence of instructions and leakage-oracle queries:
-
Let \(r_p\) be a random string long enough to specify all random choices done by the prover of \(\varPi \). For \(j\in [\rho ]\) do the following:
-
1.
Sample a random string
 ;
; -
2.
Send the query \(\big (\mathtt {X},\mathsf {Prove} (x,\cdot ,y_1,\dots ,y_j;r_p) \big )\) and let \(z_j\) be the answer to such query.
-
1.
-
Let \(\pi :=y_1,\dots ,y_\rho ,{z}_{1},\ldots ,{z}_{\rho }\) be the leaked transcript, compute the value \(j:=\mathsf {Judge}\big (x,\pi \big )\big )\), if \(j=1\) we say that the leaked argument of knowledge is accepting.
Consider the adversary \(\mathcal {A} '=({\mathcal {A} '}_{0},{\mathcal {A} '}_{1})\) that does the following:
-
1.
Pick a collision resistant hash function \(h\leftarrow {\mathsf {Gen}}^{\texttt {CRH}}(1^\kappa )\);
-
2.
Pick
 and send it to the challenger;
and send it to the challenger; -
3.
Compute h(m).
This ends the code of \({\mathcal {A} '}_0\), formally, \({\mathcal {A} '}_0(1^\kappa )\) outputs m that is forwarded to the experiment which instantiates a leakage oracle \(\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m \), also \({\mathcal {A} '}_0(1^\kappa )\) outputs the state \(st:=(h,h(m))\). Here starts the code of \({\mathcal {A} '}_1( h,h(m) )\):
-
4.
Leak Hashed Values. Define the following function:
$$ f_0(\omega \Vert m):=\left( h(L),h(R) \text{ where } L,R=\mathsf {Enc} (\mathsf {crs},m;\omega )\right) ; $$Send the query \((\mathtt {rand},f_0)\). Let \((h_l,h_r)\) be the answer to the query.
-
5.
Leak Argument of Knowledge of Consistency. Consider the following relation:
$$\mathcal {R}^{\mathsf {st}}:=\left\{ (x_{crs},x_l,x_r,x_m),(w_l,w_r): \begin{array}{c} h(w_l)=x_l\\ h(w_r)=x_r\\ h({\mathsf {Dec}}(x_{crs},w_l,w_r))=x_m \end{array}\right\} $$Leak an argument of knowledge for \((\mathsf {crs},h_l, h_r, h(m) )\in \mathcal {L}_{\mathcal {R}^{\mathsf {st}}}\) from \(\mathtt {rand} \). Notice that a witness for the instance can be defined as function of \((\omega \Vert m)\). If the leaked argument is not accepting then abort. Let \(\pi _0\) be the leaked transcript.
-
6.
Send the message encode.
-
7.
Leak Arguments of Knowledge of the Left part. Consider the following relation:
$$ \mathcal {R}^{\mathsf {hash}}:=\big \{ (y,x) : h(x)=y \big \}$$Let \(\tau := 17 \lambda _0\cdot (1+\gamma )\), for all \(i\in [\tau ]\) leak an argument of knowledge for \(h_l\in \mathcal {L}_{\mathcal {R}^{\mathsf {hash}}}\) from \(\mathtt {L} \). If the leaked argument is not accepting then abort. Let \(\pi ^L_i\) be the leaked transcript.
-
8.
Leak Arguments of Knowledge of the Right part. For all \(i\in [\tau ]\) leak an argument of knowledge for \(h_r\in \mathcal {L}_{\mathcal {R}^{\mathsf {hash}}}\) from \(\mathtt {R} \). If the leaked argument is not accepting then abort. Let \(\pi ^R_i\) be the leaked transcript.
Consider the following randomized experiment \(\mathbf {E} \):
-
Pick uniformly random
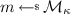 and
and  and set \(st=(h,h(m))\) and forward to the predictor the state st.
and set \(st=(h,h(m))\) and forward to the predictor the state st. -
Instantiate an oracle \(\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m \) and give the predictor access to it.
Lemma 3
\(\widetilde{\mathbb {H}}_\infty (m~ \left| \right. \mathbf {E})\geqslant \alpha - \ell _{\mathsf {CRH}} - \lambda _0\cdot (1+\gamma )\).
Proof
Consider the experiment \(\mathbf {E} '\) which is the same as \(\mathbf {E} \) except that the predictor’s input is h (instead of (h, h(m))). We apply Lemma 1:
Consider the experiment \(\mathbf {E} ''\) which is the same as \(\mathbf {E} '\) except that the predictor’s oracle access to \(\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m \) is removed. We apply Lemma 1:
In the last experiment \(\mathbf {E} ''\) the predictor has no information about m and moreover h is independently chosen with respect to m, therefore:
\(\square \)
Lemma 4
If \(\varSigma \) is \((\lambda _0,\lambda _1)\)-FLR-sim-secure then \(\widetilde{\mathbb {H}}_\infty (m|\mathbf {E})\leqslant 6\).
Proof
Assume that \(\varSigma \) is an \((\lambda _0,\lambda _1,\epsilon )\)-FLR-sim-secure split-coding scheme for a negligible function \(\epsilon \) and a slack parameter \(\gamma \). Since \(\mathcal {A} '\) is \(\mathsf {ppt}\) there exists a \(\mathsf {ppt}\) simulator \(\mathcal {S} '\) such that:
For the sake of the proof we first build a predictor which tries to guess m. We then use this predictor to prove the lemma. Let \(\mathsf {K}\) be the extractor given by the knowledge soundness property of the argument of knowledge for the relation \(\mathcal {R}^{\mathsf {hash}}\). Consider the following predictor \(\mathcal {B} \) that takes as input (h, h(m)) and has oracle access to \(\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m \):
-
1.
Pick two random tapes \(r_{a},r_{s}\) for the adversary \({\mathcal {A} '}_1\) and the simulator \(\mathcal {S} '\) and run both of them (with the respective randomness \(r_a,r_s\)) forwarding all the queries from \({\mathcal {A} '}_1\) to \(\mathcal {S} '\) and from \(\mathcal {S} '\) to \(\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m \). (The adversary \({\mathcal {A} '}_1\) starts by leaking the values \(h_l,h_r\) and an argument of knowledge for \((h_l,h_r)\in \mathcal {L}_{\mathcal {R}^{\mathsf {st}}}\). Eventually the adversary sends the message \(\mathtt {encode}\).)
-
2.L.
Extract \((h_l,L')\in \mathcal {R}^{\mathsf {hash}}\) using the knowledge extractor \(\mathsf {K}\) . For any \(i\in [\tau ]\), let \(\bar{st}^L_i\) be the actual internal state of \(\mathcal {S} '\) during the above run of \(\mathcal {S} '\) and \({\mathcal {A} '}_1\) just before the i-th iteration of step 7 of \({\mathcal {A} '}_1\).
Let \(\mathcal {P} _{\mathsf {leak}}\) be a prover of \(\varPi \) for \(\mathcal {R}^{\mathsf {hash}}\) that upon input the instance \(h_l\), randomness \(r_p\) and auxiliary input \(\bar{st}^L_i\) does the following:
-
Run a new instance \(\mathcal {S} '_i\) of \(\mathcal {S} '\) with the internal state set to \(\bar{ st }^L_i\).
-
Upon message \(y_j\) with \(j\in [\rho ]\) from the verifier, send to \(\mathcal {S} '_i\) the message \((\mathtt {L},\mathsf {Prove} (h_l,\cdot ,{y}_{1},\ldots ,{y}_{j}; r_p))\).
-
Upon message \((\mathtt {msg},f')\) from the simulator \(\mathcal {S} '_i\) reply \(\bot \) to \(\mathcal {S} '_i\).
Notice that \(\mathcal {P} _{\mathsf {leak}}\) makes no leakage oracle queries.
-
(i)
If the value \(L'\) is unset, run the knowledge extractor \(\mathsf {K}\) on the prover \(\mathcal {P} _{\mathsf {leak}}\) on input \(h_l\) and auxiliary input \(st^L_i\) and proper randomnessFootnote 1. The knowledge extractor \(\mathsf {K}\) outputs a value \(L'\) or aborts. If \(h_l= h(L')\) then set \(L'\) otherwise we say that the i-th extraction aborts.
-
(ii)
Keep on running \({\mathcal {A} '}_1\) and \(\mathcal {S} '\) as in the simulated experiment until reaching the next iteration.
If all the extractions abort, the predictor aborts.
-
-
2.R.
Extract \((h_r,R')\in \mathcal {R}^{\mathsf {hash}}\) using the knowledge extractor \(\mathsf {K}\) . The procedure is the same as step 2.L of the predictor, for notational completeness let us denote with \(st^R_i\) the internal state of \(\mathcal {S} '\) just before the i-th iteration of step 8.
-
3.
The predictor outputs \(m':={\mathsf {Dec}}(L',R')\) as its own guess.
We compute the probability that \(\mathcal {B} \) predicts m correctly. We set up some useful notation:
-
Let \(\mathsf {Ext}_L\) (resp. \(\mathsf {Ext}_R\)) be the event that \(\mathsf {K}\) successfully extracts a value \(L'\) (resp. \(R'\)).
-
Let \(\mathsf {CohSt}\) be the event \( \left\{ h({\mathsf {Dec}}(L',R'))=h(m) \right\} . \)
-
Let \(\mathsf {Coll}\) be the event \( \{h({\mathsf {Dec}}(L',R'))= h(m) \wedge {\mathsf {Dec}}(L',R')\ne m\}. \)
Recall that \(m':={\mathsf {Dec}}(L',R')\) is the guess of \(\mathcal {B} \). We can easily derive that:
In fact, \(\mathsf {Ext}_L\) and \(\mathsf {Ext}_R\) imply that \(L'\) and \(R'\) are well defined and the event \((\mathsf {CohSt}\wedge \lnot \mathsf {Coll})\) implies that \({\mathsf {Dec}}(L',R')=m\).
Claim 1
\(\Pr [\mathsf {Ext}_L] \geqslant \tfrac{1}{4} - \mathsf {negl} (\kappa )\).
Proof
Consider the execution of step 7 between the adversary and the simulator. Let \(\bar{\mathbf {st}}=\bar{st}^L_1,\dots ,\bar{st}^L_\tau \in \{0,1\}^*\) be a fixed observed value of the states of \(\mathcal {S} '\) in the different rounds, i.e., \(\bar{st}^L_i\) is the observed state of \(\mathcal {S} '\) just before the i-th iteration in step 7.
We define a probability \(\mathsf {Free}_L(\bar{st}^L_i)\) of the simulator not asking a leakage query in round i, i.e., the probability that the simulator queries its leakage oracle if run with fresh randomness starting in round i. We can assume without loss of generality that the randomness \(r_s\) of the simulator is part of \(\bar{st}^L_i\). Therefore the probability is taken over just the randomness \(r_a\) of the adversary, m, h and the challenges used in the proof in round i. Notice that even though it might be fixed in \(\bar{\mathbf {st}}=\bar{st}^L_1,\dots ,\bar{st}^L_\tau \) whether or not the simulator leaked in round i (this information might be contained in the final state \(\bar{st}^L_\tau \)), the probability \(\mathsf {Free}_L(\bar{st}^L_i)\) might not be 0 or 1, as it is the probability that the simulator leaked in round i if we would rerun round i with fresh randomness of the adversary consistent with \(\bar{st}^L_i\).
Recall that \(\bar{\mathbf {st}}=\bar{st}^L_1,\dots ,\bar{st}^L_\tau \in \{0,1\}^*\) is a fixed observed value of the states of \(\mathcal {S} '\) in the different rounds. Let \(\mathsf {Good}(\bar{\mathbf {st}})\) be a function which is 1 if
and which is 0 otherwise.Footnote 2 After having defined \(\mathsf {Good}(\bar{\mathbf {st}})\) relative to a fixed observed sequence of states, we apply it to the random variable \(\mathbf{st }\) describing the states of \(\mathcal {S} '\) in a random run. When applied to \(\mathbf{st }\), we simply write \(\mathsf {Good}\).
We use the law of total probability to condition to the event \(\{ \mathsf {Good}=1 \}\):
We will now focus on bounding \(\Pr [ \mathsf {Ext}_L ~| \mathsf {Good}=1]\cdot \Pr [\mathsf {Good}=1]\). We first bound \(\Pr [\mathsf {Good}=1]\) and then bound \(\Pr [ \mathsf {Ext}_L ~| \mathsf {Good}=1]\). We first prove that
To see this notice that the simulator by the rules of the experiment never queries its leakage oracle in more than \(\lambda _0\cdot (1+\gamma )\) rounds: it is not allowed to leak more than \(\lambda _0\cdot (1+\gamma )\) bits and each leakage query counts as at least one bit. Therefore there are at least \(\tau - \lambda _0\cdot (1+\gamma )\) rounds in which the simulator did not query its oracle. If \(\mathsf {Good}=0\), then in each of these rounds the probability of leaking, before the round was executed, was at least \(\tfrac{1}{4}\) and hence the probability of not leaking was at most \(\tfrac{3}{4}\). Set \(\lambda ':=\lambda \cdot (1+\gamma )\), we can use a union bound to bound the probability of observing this event
We now use that \(\tau = 17 \lambda _0\cdot (1+\gamma )= 17\lambda '\) and that it holds for any constant \(c \in (0,1)\) that \(\lim _{n \rightarrow \infty }{n \atopwithdelims ()c n} = 2^{H_2(c)\cdot n}\), where \(H_2\) is the binary entropy function. We get that
We now bound \(\Pr [ \mathsf {Ext}_L ~| \mathsf {Good}=1]\). Let \(\mathsf {Ext}_L(i)\) be the event that \(\mathsf {K}\) successfully extracts the value \(L'\) at the i-th iteration of the step 7 of the adversary \(\mathcal {A} \). Let \(\mathsf {Accept}_L(i)\) be the event that \(\mathcal {P} _{\mathsf {leak}}\) on input \(h_l\) and auxiliary input \(st^L_i\) gives an accepting proof. It follows from knowledge soundness of \(\varPi \) that
Let \(\mathsf {Leak}_L(i)\) be the event that the simulator queries its leakage oracle in round i. It holds for all i that
To see this assume that \(\mathcal {P} _{\mathsf {leak}}\) upon message \((\mathtt {msg},f')\) from \(\mathcal {S} '_i\) would send to the simulator \(f'(\omega \Vert m)\) instead of \(\bot \). In that case it gives an acceptable proof with probability \(1 - \mathsf {negl} (\kappa )\) as the adversary leaks an acceptable proof in the real world and the simulator simulates the real world up to negligible difference. Furthermore, sending \(\bot \) when the simulator queries its oracle can only make a difference when it actually sends a query, which happens with probability \(\Pr [\mathsf {Leak}_L(i)]\). Combining the above inequalities we get that
When \(\mathsf {Good}=1\) there exists some round \(i^*\) such that \(\mathsf {Free}_L(\bar{st}^L_{i^*}) \geqslant \frac{3}{4}\), which implies that \(\Pr \big [ \mathsf {Ext}_L(i^*) \vert \mathsf {Good}= 1 \big ] \geqslant \frac{3}{4} - \mathsf {negl} (\kappa ) - \frac{1}{2}\). Clearly \(\mathsf {Ext}_L(i^*)\) implies \(\mathsf {Ext}_L\), so we conclude that \(\Pr \big [ \mathsf {Ext}_L \vert \mathsf {Good}= 1 \big ] \geqslant \frac{1}{4} - \mathsf {negl} (\kappa )\).
Claim 2
\(\Pr [\mathsf {Ext}_R | \mathsf {Ext}_L ] \geqslant \tfrac{1}{4}-\mathsf {negl} (\kappa )\).
The proof proceeds similar to the proof of Claim 1, therefore it is omitted. The reason why the condition \(\mathsf {Ext}_L\) does not matter is that the proof exploits only the knowledge soundness of the proof system. Whether the extraction of the left part succeeded or not does not remove the knowledge soundness of the proofs for the right part, as they are done after the proofs for the left part.
Claim 3
\(\Pr [\mathsf {CohSt}~|\mathsf {Ext}_L \wedge \mathsf {Ext}_R ]\geqslant \tfrac{1}{2}- \mathsf {negl} (\kappa )\).
Proof
We reduce to the collision resistance property of h and the knowledge soundness of the argument system \(\varPi \). Suppose that
Consider the following collision finder adversary \(\mathcal {B} _{coll}(h)\):
-
1.
Sample uniformly random
 and random
and random 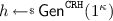 ;
; -
2.
Run an instance of the predictor \(\mathcal {B} ^{\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m}(h,h(m))\). The predictor needs oracle access to \(\mathcal {O} _{\lambda _0\cdot (1+\gamma )}^m \) which can be simulated by \(\mathcal {B} _{coll}(h)\).
-
3.
Let \(L',R'\) be defined as by the execution of the predictor \(\mathcal {B} \) and let \(r_a,r_s\) be the same randomness used by \(\mathcal {B} \) in its step 1. Simulate an execution of \(\mathcal {A} _1(h,h(m);r_a)\) and \(\mathcal {S} '(1^\kappa ;r_s)\) and break them just before the adversary leaks an argument of knowledge for \(\mathcal {R}^{\mathsf {st}}\). Let \(st'\) be the internal state of \(\mathcal {S} (1^\kappa ;r_s)\). Let \(\mathcal {P} _{\mathsf {leak}}'\) be a prover for \(\varPi \) for the relation \(\mathcal {R}^{\mathsf {st}}\) that upon input the instance \((\mathsf {crs},h(L'),h(R'),h(m))\) and auxiliary input \(z:=(st',m)\) does the following:
-
Run an \(\mathcal {S} '\) with the internal state set to \(st'\). Sample a random string \(r_p\) long enough to specify all random choices done by the prover of \(\varPi \).
-
Upon message \(y_j\) with \(j\in [\rho ]\) from the verifier, send to \(\mathcal {S} '\) the message \((\mathtt {rand},\mathsf {Prove} ((\mathsf {crs},h(L'),h(R'),h(m)),\mathsf {Enc} (\mathsf {crs},\cdot \ ;\cdot ),{y}_{1},\ldots ,{y}_{j};r_p))\). (The next-message function of the prover of \(\varPi \) that uses as input the witness \(\mathsf {Enc} (\mathsf {crs},m;\omega )\) and the internal randomness set to \(r_p\).)
-
Upon message \((\mathtt {msg},f')\) from the simulator \(\mathcal {S} '\) reply forwarding \(f'(m)\).
-
-
4.
Run \(\mathsf {K}_{\mathsf {st}}\) on the prover \(\mathcal {P} _{\mathsf {leak}}'\) on input \((\mathsf {crs},h(L'),h(R'), h(m))\) and auxiliary input z. Let \(L'',R''\) be the witness output by the extractor.
-
5.
If \(L'\ne L''\) output \((L',L'')\) else \((R',R'')\).
It is easy to check that \(\mathcal {B} _{coll}\) simulates perfectly the randomized experiment \(\mathbf {E} \). Therefore:
On the other hand, the extractor \(\mathsf {K}_{\mathsf {st}}\) succeeds with probability at least \(1-\mathsf {negl} (\kappa ) - \tfrac{1}{2}\). Therefore, \(L''\) and \(R''\) are such that \(h(L'')= h(L')\), \(h(R'')= h(R')\) and \(h({\mathsf {Dec}}(L'',R''))=h(m)\).
Combining the latter and the statement of the event in Eq. (5), we have \(h({\mathsf {Dec}}(L',R'))\ne h(m)= h({\mathsf {Dec}}(L'',R''))\) which implies that either \(L'' \ne L'\) or \(R'' \ne R'\). Lastly, notice that \(\mathcal {B} _{coll}\) is an expected polynomial time algorithm. However we can make it polynomial time by aborting if the number of step exceeds some fixed polynomial. By setting the polynomial big enough the probability of \(\mathcal {B} _{coll}\) finding a collision is still noticeable.
Claim 4
\(\Pr \big [\mathsf {Coll}~| \mathsf {CohSt}\wedge \mathsf {Ext}_L \wedge \mathsf {Ext}_R \big ] \leqslant \mathsf {negl} (\kappa )\).
Recall that \(\mathsf {Coll}\) is the event that \(h(m)=h(m')\) but \(m\ne m'\). It can be easily verified that under collision resistance of h the claim holds, therefore the proof is omitted. Summarizing, we have:
which implies the statement of the lemma.
We conclude the proof of the theorem noticing that, if \(\varSigma \) is \((\lambda _0,\lambda _1)\)-FLR-sim-secure split-coding scheme by the parameter given in the statement of the theorem we have that Lemmas 3 and 4 are in contraction. \(\square \)
Remark 1
The result can be generalized for a weaker version of the split-state model where the codeword is split in many parts. The probability that the predictor in Lemma 4 guesses the message m degrades exponentially in the number of splits (the adversary needs to leak one hash for each split and then executes step 7 for any split). Therefore, the impossibility holds when the number of splits is \(o((\alpha - \lambda _0(1+\gamma ))/\ell _\mathsf {CRH})\). We present the theorem, as stated here, for sake of simplicity.
The Case of Constant-Size Message. For space reason we defer the impossibility result for the case of constant-size message fully leakage resilient codes the full version of the paper [18].
5 Feasibility Results
In this section we give two feasibility results for weaker models of security.
5.1 The Inner-Product Extractor is a \(\mathsf {NC}^0\)-Fully LR Code
We start by giving a well-known characterization of the class \(\mathsf {NC}^0\).
Lemma 5
Let \(f\in \mathsf {NC}^0\) where \(f:=\left( f^n:\{0,1\}^n\rightarrow \{0,1\}^{m(n)}\right) _{n\in \mathbb N}\) for a function m. For any n there exists a value \(c=O(m)\), a set \(\{{i}_{1},\ldots ,{i}_{c}\}\subseteq [n]\) of indexes and a function g such that for any \(x\in \{0,1\}^n\), \(f(x)=g(x_{i_1},x_{i_2},\dots ,x_{i_c})\).
The lemma above shows that any function in \(\mathsf {NC}^0\) with output length m such that \(m(n)/n =o(1)\) cannot be collision resistant, because an adversary can guess an index \(i\notin \{{i}_{1},\ldots ,{i}_{c}\}\) and output \(0^n,(0^{i-1}\Vert 1\Vert 0^{n-i})\) as collision.
Let \(\mathbb {F} \) be a finite field and let \(\varPhi ^{n}_\mathbb {F} =(\mathsf {Enc},{\mathsf {Dec}})\) be as follows:
-
\(\mathsf {Enc} \) on input \(m\in \mathbb {F} \) picks uniformly random
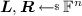 under the condition that \(\left\langle {\varvec{L},\varvec{R}} \right\rangle =m\).
under the condition that \(\left\langle {\varvec{L},\varvec{R}} \right\rangle =m\). -
\({\mathsf {Dec}}\) on input \(\varvec{L},\varvec{R}\) outputs \(\left\langle {\varvec{L},\varvec{R}} \right\rangle \).
Theorem 2
(from [15]). The encoding scheme \(\varPhi ^{n}_\mathbb {F} \) as defined above for \(|\mathbb {F} |=\varOmega (\kappa )\) is a \((0,0.3\cdot n\log |\mathbb {F} ||)\)-FLR-SIM-secure for \(n>20\).
We will show now that the scheme is also fully leakage resilient for \(\mathsf {NC}^0\)-bounded adversaries.
Theorem 3
For any \(n\in \mathbb N\) and \(n>20\) there exists a positive constant \(\delta \in \mathbb {R}\) such that, for any \(\lambda _0,\lambda _1\) such that \(\delta \cdot \lambda _0+\lambda _1< 0.3\cdot |\mathbb {F} ^n|\) the encoding scheme \(\varPhi ^n_\mathbb {F} \) is \((\mathsf {NC}^0,\lambda _0,\lambda _1)\)-FLR-SIM-secure.
We reduce an adversary \(\mathcal {A} \) for the \((\mathsf {NC}^0,\lambda _0,\lambda _1)\)-FLR-SIM game (with \(\lambda _0>0\)) to an adversary for the \((0,\delta \cdot \lambda _0+\lambda _1)\)-FLR-SIM game. Given Lemma 5 and the structure of \(\varPhi ^n_\mathbb {F} \), the task is very easy. In fact, the randomness \(\omega \) picked by \(\mathsf {Enc} \) can be parsed as \(({L}_{0},\ldots ,{L}_{n-1},{R}_{0},\ldots ,{R}_{n-2})\). Whenever the adversary \(\mathcal {A} \) queries the oracle \(\mathcal {O} _{\lambda _0}^\omega \) the reduction splits the leakage function in two pieces and leak from \(\mathcal {O} ^\mathbf{L}\) and \(\mathcal {O} ^\mathbf{R}\) the relative piece of information necessary to compute the leakage function. Because of Lemma 5 we know that for each function the amount of leakage done on the two states is bounded by a constant \(\delta \).
Proof
Given a vector \(\varvec{X}\in \mathbb {F} ^n\) let \(\mathsf {bit}(X)_i\) be the i-th bit of a canonical bit-representation of \(\varvec{X}\). Given \(\mathcal {A} =(\mathcal {A} _0,\mathcal {A} _1)\) we define a new adversary \(\mathcal {A} '\) that works as follows:
-
0.
Instantiate an execution of
 ;
; -
1.
Execute \(\mathcal {A} _1(st)\) and reply to the leakage oracle queries it makes as follow:
-
Upon message \((\mathtt {rand},f)\) from \(\mathcal {A} _1\), let I be the set of indexes such that f depends on I only. Define \(I_L := I \cap [qn]\) and \(I_R := I\cap [qn+1,2qn]\). Define the functions:
$$f_L(\varvec{L}):= (\mathsf {bit}(\varvec{L})_i \text{ for } i\in I_L) \text{ and } f_R(\varvec{R}):= (\mathsf {bit}(\varvec{R})_i \text{ for } i\in I_R).$$Send the queries \((\mathtt {L},f_L)\) and \((\mathtt {R},f_R)\) and let \(\mathsf {lk}_L\) and \(\mathsf {lk}_R\) be the answers to the queries. Hardwire such values and evaluate the function f on input m. Namely, compute \(\mathsf {lk}_f:=f( f_L(\varvec{L}), f_R(\varvec{R}), m)\) and send it back to \(\mathcal {A} _1(st)\).
-
Upon message \((\mathtt {X},f)\) where \(\mathtt {X}\in \{\mathtt {L},\mathtt {R} \}\) from \(\mathcal {A} _1\) forward the message.
-
W.l.o.g. assume that every leakage query to \(\mathcal {O} _{\lambda _0}^{\omega \Vert m} \) has output length 1 and that the adversary makes exactly \(\lambda _0\) queries. By Lemma 5 there exists a constant \(\delta \in \mathbb N\) such that for the i-th leakage query made by \(\mathcal {A} _1\) to \(\mathcal {O} _{\lambda _0}^{\omega \Vert m} \) the adversary \(\mathcal {A} '\) leaks \(\delta \) bits from \(\mathcal {O} _{\lambda _1}^L,\mathcal {O} _{\lambda _1}^R \). By construction:
Let \(\mathcal {S} '\) be the simulator for the adversary \(\mathcal {A} '\) as provided by Theorem 2, thus:
Let \(\mathcal {S} \) be defined as the machine that runs the adversary \(\mathcal {A} '\) interacting with the simulator \(\mathcal {S} '\). Notice that:
This conclude the proof of the theorem. \(\square \)
The proof exploits only marginally the structure of \(\varPhi ^{n}_\mathbb {F} \). It is not hard to see that the theorem can be generalized for any coding scheme \(({\mathsf {Gen}},\mathsf {Enc},{\mathsf {Dec}})\) where for any message \(m\in \mathcal {M}\) and any \(\mathsf {crs}\) the function \(\mathsf {Enc} (\mathsf {crs},m;\cdot )\) is invertible in \(\mathsf {NC}^0\). We present the theorem, as stated here, only for sake of concreteness. Moreover, the The construction is secure under the slightly stronger definition where the adversary does not lose access to \(\mathcal {O} _{\lambda _0}^{\omega \Vert m} \) after having sent the message encode.
5.2 A Compiler from LRC to FLRC
Given a \((\alpha ,\beta )\)-split-coding scheme \(\varSigma =({\mathsf {Gen}},\mathsf {Enc},{\mathsf {Dec}})\) with randomness space \(\mathcal {R} \), let \(\mathcal {H} _{r,t}\) denote a family of efficiently computable t-wise independent hash function with domain \(\{0,1\}^{r}\) and co-domain \(\mathcal {R} \). We define \(\varSigma '=({\mathsf {Gen}}',\mathsf {Enc} ',{\mathsf {Dec}}':={\mathsf {Dec}})\):
-
\({\mathsf {Gen}}'\) on input \(1^\kappa \) executes
 and samples a function
and samples a function 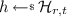 . It outputs \(\mathsf {crs}' = (h,\mathsf {crs})\).
. It outputs \(\mathsf {crs}' = (h,\mathsf {crs})\). -
\(\mathsf {Enc} '\) on input a message \(m\in \mathcal {M}\) and \((h,\mathsf {crs})\) picks a random string
 and returns as output \(\mathsf {Enc} (\mathsf {crs},m;h(\omega ))\).
and returns as output \(\mathsf {Enc} (\mathsf {crs},m;h(\omega ))\).
Theorem 4
For any encoding scheme \(\varSigma \) and any leakage class \(\mathcal {F} \), if \(\varSigma \) is \((0,\lambda _1,\epsilon )\)-FLR-SIM-secure then \(\varSigma '\) is \((\mathcal {F},\lambda _0,\lambda _1,3\epsilon )\)-FLR-SIM-secure for any \(0\leqslant \lambda _0 < \alpha \) whenever:
We leverage on the fact that with overwhelming probability a t-wise independent hash function (where t is set as in the statement of the theorem) is a deterministic strong randomness extractor for the class of of sources defined by adaptively leaking from the randomness using functions from \(\mathcal {F} \). We can, therefore, reduce an adversary for the \((\mathcal {F},\lambda _0,\lambda _1)\)-FLR-SIM game to an adversary for the \((0,\lambda _1)\)-FLR-SIM game. The reduction samples a uniformly random string  and replies all the leakage oracle queries on the randomness by applying the the leakage function on \(\omega '\). By the property of the randomness extractor, this leakage is indistinguishable from to the leakage on the real randomness. It is not hard to see that the above result can be generalized to every class of leakage that allows an efficient average-case strong randomness extractor [14]. We present the result, as stated here, only for sake of concreteness.
and replies all the leakage oracle queries on the randomness by applying the the leakage function on \(\omega '\). By the property of the randomness extractor, this leakage is indistinguishable from to the leakage on the real randomness. It is not hard to see that the above result can be generalized to every class of leakage that allows an efficient average-case strong randomness extractor [14]. We present the result, as stated here, only for sake of concreteness.
Proof
Given an adversary \(\mathcal {A} '\) against \(\varSigma '\), we define a \(\mathsf {ppt}\) adversary \(\mathcal {A} =(\mathcal {A} _0,\mathcal {A} _1)\) against \(\varSigma \) as follow:
-
Adversary \(\mathcal {A} _0\) : On input \(\mathsf {crs}\), it picks at random
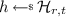 , a random string
, a random string 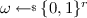 and a random string
and a random string  for a polynomial p that bounds the running time of \(\mathcal {A} '\) and runs \({\mathcal {A} '}_0(1^\kappa ;r)\). Upon leakage oracle query f to \({\mathcal {O} _{\lambda _0}^{\omega }}\) from \({\mathcal {A} '}_0\), it replies \(f(\omega )\). Eventually, the adversary \({\mathcal {A} '}_0\) outputs a a message \(m\in \mathcal {M} \) and a state value st, \(\mathcal {A} _0\) outputs m and \(st'=(st,h)\).
for a polynomial p that bounds the running time of \(\mathcal {A} '\) and runs \({\mathcal {A} '}_0(1^\kappa ;r)\). Upon leakage oracle query f to \({\mathcal {O} _{\lambda _0}^{\omega }}\) from \({\mathcal {A} '}_0\), it replies \(f(\omega )\). Eventually, the adversary \({\mathcal {A} '}_0\) outputs a a message \(m\in \mathcal {M} \) and a state value st, \(\mathcal {A} _0\) outputs m and \(st'=(st,h)\). -
Adversary \(\mathcal {A} _1\) : On inputs \(st'=(st,h)\) and \(\mathsf {crs}\), it runs \({\mathcal {A} '}_1(st,(h,\mathsf {crs}))\) and forwards all the queries made by \({\mathcal {A} '}_1\).
W.l.o.g. the adversary \(\mathcal {A} _0\) makes the sequence \((\mathtt {rand},f_1),(\mathtt {rand} ,f_2),\dots ,(\mathtt {rand},f_{\lambda _0})\) of queries. Let \(\varvec{f}:=({f}_{1},\ldots ,{f}_{\lambda _0}) \in \mathcal {F} ^{\lambda _0}\), therefore view of \(\mathcal {A} '\) in the real experiment is:
On the other hand, by definition of the adversary \(\mathcal {A} \), the view provided to \(\mathcal {A} '\) is:
where \({L'},{R'}=\mathsf {Enc} (\mathsf {crs},m;\omega ')\) and  and
and  .
.
Claim 5
\( \big \{{{\mathsf {Real}}_{\mathcal {A} ',\varSigma '}^{\lambda _0,\lambda _1}}(\kappa )\big \}_{\kappa \in \mathbb N} \approx _{2\epsilon (\kappa )} \big \{\mathsf {Hyb}(\kappa )\big \}_{\kappa \in \mathbb N} \).
Before proceeding with the proof of the claim we show how the theorem follows. Let \(\mathcal {S} \) be the simulator for the adversary \(\mathcal {A} \) as given by the hypothesis of the theorem:
Let \(\mathcal {S} '\) be defined as the adversary \(\mathcal {A} \) interacting with the simulator \(\mathcal {S} \). Therefore, if we consider \(\mathsf {Ideal}^{0,\lambda _1}_{\mathcal {A},\mathcal {S}}(\kappa )=\big ( (r,h,\omega ),\ \mathsf {crs}, \widetilde{\mathsf {lk}}_L, \widetilde{\mathsf {lk}}_R \big )\), it holds that:
It follows from a simple reduction to Eq. (6) that:
We conclude by applying Claim 5 to equation above. \(\square \)
Proof
(of the claim). Since we are proving statistical closeness we can de-randomize the adversary \(\mathcal {A} '\) by setting the random string that maximize the distinguishability of the two random variables. Similarly we can de-randomize the common reference string generation algorithm \({\mathsf {Gen}}\). Therefore, w.l.o.g., we can consider them fixed in the views.
Recall that the adversary \(\mathcal {A} \) defines for \(\mathcal {A} '\) a hybrid environment where the leakage on the randomness is on  but the codeword is instantiated using fresh randomness
but the codeword is instantiated using fresh randomness  . We prove the stronger statement that the two views are statistical close with high probability over the choice of the t-wise hash function h. For convenience, we define two tuples of random variables:
. We prove the stronger statement that the two views are statistical close with high probability over the choice of the t-wise hash function h. For convenience, we define two tuples of random variables:
Notice that in both distributions above the function \(\varvec{f}\) are random variable. For any fixed sequence of functions \(\varvec{f} = {f}_{0},\ldots ,{f}_{\lambda _0}\), let \(\mathsf {Real}_{h,\varvec{f}}\) (resp. \(\mathsf {Hyb}_{h,\varvec{f}}\)) be the distribution \(\mathsf {Real}_{h}\) (resp. \(\mathsf {Hyb}_{h}\)) where the leakage functions are set. We prove that
where the probability is over the choice of  . Let \(\mathsf {Bad}\) be the event \(\{\mathsf {Hyb}_{h} \not \approx _\epsilon \mathsf {Real}_{h}\}\).
. Let \(\mathsf {Bad}\) be the event \(\{\mathsf {Hyb}_{h} \not \approx _\epsilon \mathsf {Real}_{h}\}\).

Let \(\lambda :=\lambda _0+\lambda _1\) and let \(p_{v}:=\Pr _{\omega ,\omega '}[\mathsf {Hyb}_{h,\varvec{f}} = v]\). Define \(\tilde{p}_v := \max \{ p_v, 2^{-\lambda }\}\). Note that:
Define the indicator random variable \(Y_{\bar{\omega },v}\) for the event \(\{\mathsf {Real}_{h,\varvec{f}}= v~|\omega = \bar{\omega }\}\), where the randomness is over the choice of  .
.
For any view v, the random variables \(\{ Y_{\bar{\omega },v} \}_{\bar{\omega }\in \{0,1\}^r}\) are t-wise independent.
Moreover, \({{\mathrm{\mathbb {E}}}}[\sum _{\bar{\omega }\in \{0,1\}^r} Y_{\bar{\omega },v}]=2^rp_{v}\). In fact, for any \(\bar{h}\in \mathcal {H} \), any \(\bar{\omega }\in \{0,1\}^r\) and any \(v\in \{0,1\}^\lambda \) it holds that \(\Pr _h[\mathsf {Real}_{h,\varvec{f}}= v~|\omega = \bar{\omega }]=\Pr _{\omega '}[\mathsf {Hyb}_{h,\varvec{f}}=v~|\omega = \bar{\omega }, h = \bar{h}]\). It follows that

where Eq. (7) follows by Lemma 2 and Eqs. (8) and (9) follow because \(2^{r}\cdot \tilde{p}_v\geqslant 2^{r-\lambda }\geqslant t\). Combining all together we have:
To make the above negligible we can set:
6 Conclusion and Open Problems
We defined the notion of Fully Leakage Resilient Codes. Although natural, our definition is too strong to be met in the popular split-state model. Fortunately, by restricting the class of leakage from the randomness we were able to achieve two different feasibility results.
There is still a gap between our impossibility result and the possibility results. As we showed, in the plain model the problem of finding a FLR Code in the split-state model is strictly connected to the complexity of computing the next-message function of a prover of a succinct argument of knowledge and to the complexity of computing an collision resistant hash function. A construction of FLR code for, let say, the class \(\mathsf {NC}\) provides, therefore, a complexity lower bound for at least one of the two mentioned tasks and it would be a very surprising result. An interesting open problem is to show FLR codes for \(\mathsf {AC}^0\).
Our definition restricts the simulator to be efficient, this seems a natural restriction and it is necessary for our impossibility result. It would be interesting to show either a FLR code with unbounded-time simulator or to generalize our impossibility result in this setting.
Notes
- 1.
The randomness for \(\mathcal {P} _{\mathsf {leak}}\) is implicitly defined in the random string \(r_a\).
- 2.
Intuitively, \(\mathsf {Good}\) is an indicator for a good event, that, as we will show, has overwhelming probability.
References
Aggarwal, D., Dziembowski, S., Kazana, T., Obremski, M.: Leakage-resilient non-malleable codes. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 398–426. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_17
Alwen, J., Dodis, Y., Wichs, D.: Leakage-resilient public-key cryptography in the bounded-retrieval model. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 36–54. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_3
Ananth, P., Boneh, D., Garg, S., Sahai, A., Zhandry, M.: Differing-inputs obfuscation and applications. Cryptology ePrint Archive, Report 2013/689 (2013). http://ia.cr/2013/689
Ananth, P., Goyal, V., Pandey, O.: Interactive proofs under continual memory leakage. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 164–182. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44381-1_10
Andrychowicz, M., Masny, D., Persichetti, E.: Leakage-resilient cryptography over large finite fields: theory and practice. In: Malkin, T., Kolesnikov, V., Lewko, A.B., Polychronakis, M. (eds.) ACNS 2015. LNCS, vol. 9092, pp. 655–674. Springer, Heidelberg (2015). doi:10.1007/978-3-319-28166-7_32
Bellare, M., Rompel, J.: Randomness-efficient oblivious sampling. In: FOCS, pp. 276–287 (1994)
Bitansky, N., Canetti, R., Halevi, S.: Leakage-tolerant interactive protocols. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 266–284. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28914-9_15
Bitansky, N., Dachman-Soled, D., Lin, H.: Leakage-tolerant computation with input-independent preprocessing. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 146–163. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44381-1_9
Boyle, E., Chung, K.-M., Pass, R.: On extractability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 52–73. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_3
Boyle, E., Goldwasser, S., Kalai, Y.T.: Leakage-resilient coin tossing. Distrib. Comput. 27(3), 147–164 (2014)
Boyle, E., Segev, G., Wichs, D.: Fully leakage-resilient signatures. J. Cryptol. 26(3), 513–558 (2013)
Davì, F., Dziembowski, S., Venturi, D.: Leakage-resilient storage. In: Garay, J.A., Prisco, R. (eds.) SCN 2010. LNCS, vol. 6280, pp. 121–137. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15317-4_9
Dodis, Y., Lewko, A.B., Waters, B., Wichs, D.: Storing secrets on continually leaky devices. In: FOCS, pp. 688–697 (2011)
Dodis, Y., Ostrovsky, R., Reyzin, L., Smith, A.D.: Fuzzy extractors: how to generate strong keys from biometrics and other noisy data. SIAM J. Comput. 38(1), 97–139 (2008)
Dziembowski, S., Faust, S.: Leakage-resilient cryptography from the inner-product extractor. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 702–721. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25385-0_38
Dziembowski, S., Pietrzak, K.: Leakage-resilient cryptography. In: FOCS, pp. 293–302 (2008)
Dziembowski, S., Pietrzak, K., Wichs, D.: Non-malleable codes. In: ICS, pp. 434–452 (2010)
Faonio, A., Nielsen, J.B.: Fully leakage-resilient codes. IACR Cryptology ePrint Archive 2015:1151 (2015)
Faonio, A., Nielsen, J.B., Venturi, D.: Mind your coins: fully leakage-resilient signatures with graceful degradation. IACR Cryptology ePrint Archive 2014:913 (2014)
Faonio, A., Nielsen, J.B., Venturi, D.: Predictable arguments of knowledge (2015). http://ia.cr/2015/740
Faust, S., Mukherjee, P., Nielsen, J.B., Venturi, D.: Continuous non-malleable codes. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 465–488. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_20
Faust, S., Mukherjee, P., Nielsen, J.B., Venturi, D.: A tamper and leakage resilient von neumann architecture. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 579–603. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_26
Faust, S., Mukherjee, P., Venturi, D., Wichs, D.: Efficient non-malleable codes and key-derivation for poly-size tampering circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 111–128. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_7
Faust, S., Rabin, T., Reyzin, L., Tromer, E., Vaikuntanathan, V.: Protecting circuits from leakage: the computationally-bounded and noisy cases. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 135–156. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_7
Garg, S., Gentry, C., Halevi, S., Wichs, D.: On the implausibility of differing-inputs obfuscation and extractable witness encryption with auxiliary input. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 518–535. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_29
Garg, S., Jain, A., Sahai, A.: Leakage-resilient zero knowledge. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 297–315. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22792-9_17
Halevi, S., Lin, H.: After-the-fact leakage in public-key encryption. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 107–124. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_8
Heyse, S., Kiltz, E., Lyubashevsky, V., Paar, C., Pietrzak, K.: Lapin: an efficient authentication protocol based on ring-lpn. In: Canteaut, A. (ed.) FSE 2012. LNCS, vol. 7549, pp. 346–365. Springer, Heidelberg (2012). doi:10.1007/978-3-642-34047-5_20
Jafargholi, Z., Wichs, D.: Tamper detection and continuous non-malleable codes. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 451–480. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_19
Katz, J., Vaikuntanathan, V.: Signature schemes with bounded leakage resilience. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 703–720. Springer, Heidelberg (2009). doi:10.1007/978-3-642-10366-7_41
Kilian, J.: A note on efficient zero-knowledge proofs and arguments (extended abstract). In: STOC, pp. 723–732 (1992)
Kocher, P.C.: Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 104–113. Springer, Heidelberg (1996). doi:10.1007/3-540-68697-5_9
Kocher, P., Jaffe, J., Jun, B.: Differential power analysis. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 388–397. Springer, Heidelberg (1999). doi:10.1007/3-540-48405-1_25
Liu, F.-H., Lysyanskaya, A.: Tamper and leakage resilience in the split-state model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 517–532. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_30
Malkin, T., Teranishi, I., Vahlis, Y., Yung, M.: Signatures resilient to continual leakage on memory and computation. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 89–106. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_7
Micali, S., Reyzin, L.: Physically observable cryptography. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 278–296. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24638-1_16
Naor, M., Segev, G.: Public-key cryptosystems resilient to key leakage. IACR Cryptology ePrint Archive 2009:105 (2009)
Nielsen, J.B., Venturi, D., Zottarel, A.: On the connection between leakage tolerance and adaptive security. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 497–515. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36362-7_30
Nielsen, J.B., Venturi, D., Zottarel, A.: Leakage-resilient signatures with graceful degradation. In: Public Key Cryptography, pp. 362–379 (2014)
Ostrovsky, R., Persiano, G., Visconti, I.: Impossibility of black-box simulation against leakage attacks. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 130–149. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_7
Pandey, O.: Achieving constant round leakage-resilient zero-knowledge. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 146–166. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_7
Quisquater, J.-J., Samyde, D.: Electromagnetic analysis (EMA): measures and counter-measures for smart cards. In: E-smart, pp. 200–210 (2001)
Trevisan, L., Vadhan, S.P.: Extracting randomness from samplable distributions. In: FOCS, pp. 32–42 (2000)
Wee, H.: On round-efficient argument systems. In: Caires, L., Italiano, G.F., Monteiro, L., Palamidessi, C., Yung, M. (eds.) ICALP 2005. LNCS, vol. 3580, pp. 140–152. Springer, Heidelberg (2005). doi:10.1007/11523468_12
Acknowledgement
The authors acknowledge support by European Research Council Starting Grant 279447. The authors acknowledge support from the Danish National Research Foundation and The National Science Foundation of China (under the grant 61361136003) for the Sino-Danish Center for the Theory of Interactive Computation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Faonio, A., Nielsen, J.B. (2017). Fully Leakage-Resilient Codes. In: Fehr, S. (eds) Public-Key Cryptography – PKC 2017. PKC 2017. Lecture Notes in Computer Science(), vol 10174. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54365-8_14
Download citation
DOI: https://doi.org/10.1007/978-3-662-54365-8_14
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54364-1
Online ISBN: 978-3-662-54365-8
eBook Packages: Computer ScienceComputer Science (R0)





 , P on inputs x, w samples uniformly random string
, P on inputs x, w samples uniformly random string 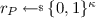 .
. and randomness
and randomness  for a polynomial p that bounds the running time of
for a polynomial p that bounds the running time of  ;
; and send it to the challenger;
and send it to the challenger;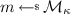 and
and  and set
and set  and random
and random 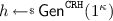 ;
;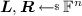 under the condition that
under the condition that  ;
; and samples a function
and samples a function 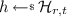 . It outputs
. It outputs  and returns as output
and returns as output 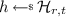 , a random string
, a random string 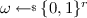 and a random string
and a random string  for a polynomial p that bounds the running time of
for a polynomial p that bounds the running time of