Abstract
Refinement types turn typechecking into lightweight verification. The classic form of refinement type is the datasort refinement, in which datasorts identify subclasses of inductive datatypes.
Existing type systems for datasort refinements require that all the refinements of a type be specified when the type is declared; multiple refinements of the same type can be obtained only by duplicating type definitions, and consequently, duplicating code.
We enrich the traditional notion of a signature, which describes the inhabitants of datasorts, to allow re-refinement via signature extension, without duplicating definitions. Since arbitrary updates to a signature can invalidate the inversion principles used to check case expressions, we develop a definition of signature well-formedness that ensures that extensions maintain existing inversion principles. This definition allows different parts of a program to extend the same signature in different ways, without conflicting with each other. Each part can be type-checked independently, allowing separate compilation.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Type systems provide guarantees about run-time behaviour; for example, that a record will not be multiplied by a string. However, the guarantees provided by traditional type systems like Hindley–Milner do not rule out a practically important class of run-time failures: nonexhaustive match exceptions. For example, the type system of Standard ML allows a case expression over lists that omits a branch for the empty list:

If this expression is evaluated with elems bound to the empty list [], the exception Match will be raised.
Datasort refinements eliminate this problem: a datasort can express, within the static type system, that elems is not empty; therefore, the above case expression will never raise Match. Datasorts can also express less shallow properties. For example, the definition in Fig. 1 encodes conjunctive normal form—a formula that consists of (possibly nested) \(\mathsf {And}\)s of clauses, where a clause consists of (possibly nested) \(\mathsf {Or}\)s of literals, where a literal is either a positive literal (a variable) or a negation of a positive literal. A case expression comparing two values of type \(\mathsf {clause}\) would only need branches for \(\mathsf {Or}\), \(\mathsf {Not}\) and \(\mathsf {Var}\); the \(\mathsf {And}\) branch could be omitted, since \(\mathsf {And}\) does not produce a \(\mathsf {clause}\).
Datasorts correspond to regular tree grammars, which can encode various data structure invariants (such as the colour invariant of red-black trees), as well as properties such as CNF and A-normal form. Datasort refinements are less expressive than the “refinement type” systems (such as liquid types) that followed work on index refinements and indexed types; like regular expressions, which “can’t count”, datasorts cannot count the length of a list or the height of a tree. However, types with datasorts are simpler in some respects; most importantly, types with datasorts never require quantifiers. Avoiding quantifiers, especially existential quantifiers, also avoids many complications in type checking. By analogy, regular expressions cannot solve every problem—but when they can solve the problem, they may be the best solution.
The goal of this paper is to make datasort refinements more usable—not by making datasorts express more invariants, but by liberating them from the necessity of a fixed specification (a fixed signature). First, we review the trajectory of research on datasorts.
The first approach to datasort refinements (Freeman and Pfenning 1991; Freeman 1994) extended ML, using abstract interpretation (Cousot and Cousot 1977) to infer refined types. The usual argument in favour of type inference is that it reduces a direct burden on the programmer. When type annotations are boring or self-evident, as they often are in plain ML, this argument is plausible. But datasorts can express more subtle specifications, calling that argument into question. Moreover, inference discourages a form of fine-grained modularity. Just as we expect a module system to support information hiding, so that clients of a module cannot depend on its internal details, a type system should prevent the callers of a function from depending on its internal details. Inferring refinements exposes those details. For example, if a function over lists is written with only nonempty input in mind, the programmer may not have thought about what the function should do for empty input, so the type system shouldn’t let the function be applied to an empty list. Finally, inferring all properties means that the inferred refined types can be long, e.g. inferring a 16-part intersection type for a simple function (Freeman and Pfenning 1991, p. 271).
Thus, the second generation of work on datasort refinements (Davies and Pfenning 2000; Davies 2005) used bidirectional typing, rather than inference. Programmers have to write more annotations, but refinement checking will never fabricate unintended invariants. A third generation of work (Dunfield and Pfenning 2004; Dunfield 2007b) stuck with bidirectional type checking, though this was overdetermined: other features of that type system made inference untenable.
All three generations (and later work by Lovas (2010) on datasorts for LF) shared the constraint that a given datatype could be refined only once. The properties tracked by datasorts could not be subsequently extended; the same set of properties must be used throughout the program. Modular refinement checking could be achieved only by duplicating the type definition and all related code. Separate type-checking of refinements enables simpler reasoning about programs, separate compilation, and faster type-checking (simpler refinement relations lead to simpler case analyses).
The history of pattern typing in case expressions is also worth noting, as formulating pattern typing seems to be the most difficult step in the design of datasort type systems. Freeman supported a form of pattern matching that was oversimplified. Davies implemented the full SML pattern language and formalized most of it, but omitted as-patterns—which become nontrivial when datasort refinements enter the picture.
The system in this paper allows multiple, separately declared refinements of a type by revising a fundamental mechanism of datasort refinements: the signature. Refinements are traditionally described using a signature that specifies—for the entire program—which values of a datatype belong to which refinements. For example, the type system can track the parity of bitstrings using the following signature, which says: (1) \(\mathsf {even}\) and \(\mathsf {odd}\) are subsorts (subtypes) of the type \(\mathsf {bits}\) of bitstrings, the (2) empty bitstring has even parity, (3) appending a 1 flips the parity, and (4) appending a 0 preserves parity.

The connective  , read “and” or “intersection”, denotes conjunction of properties: adding a \(\mathsf {One}\) makes an even bitstring odd (
, read “and” or “intersection”, denotes conjunction of properties: adding a \(\mathsf {One}\) makes an even bitstring odd ( ), and makes an odd bitstring even (
), and makes an odd bitstring even ( ). Thus, if
). Thus, if  is a bitstring known to have odd parity, then appending a 1 yields a bitstring with even parity:
is a bitstring known to have odd parity, then appending a 1 yields a bitstring with even parity:

In some datasort refinement systems (Dunfield 2007b; Lovas 2010), the programmer specifies the refinements by writing a signature like the one above. In the older systems of Freeman and Davies, the programmer writes a regular tree grammarFootnote 1, from which the system infers a signature, including the constructor types and the subsort relation:

In either design, the typing phase uses the same form of signature. We use the first design, where the programmer gives the signature directly. Giving the signature directly is more expressive, because it enables refinements to carry information not present at run time. For example, we can refine natural numbers by \(\mathsf {Tainted}\) and \(\mathsf {Untainted}\):

The sorts  and
and  have the same closed inhabitants, but a program cannot directly create an instance of
have the same closed inhabitants, but a program cannot directly create an instance of  from an instance of
from an instance of  :
:

Thus, the two sorts have different open inhabitants. This is analogous to dimension typing, where an underlying value is just an integer or float, but the type system tracks that the number is in (for example) metres (Kennedy 1996).
Giving the signature directly allows programmers to choose between a variety of subsorting relationships. For example, to allow untainted data to be used where tainted data is expected, write  . Subsorting can be either structural (as the signatures generated from grammars) or nominal (as in the example above). In this paper, giving signatures directly is helpful: it enables extension of signatures without translating between signatures and grammars.
. Subsorting can be either structural (as the signatures generated from grammars) or nominal (as in the example above). In this paper, giving signatures directly is helpful: it enables extension of signatures without translating between signatures and grammars.
Contributions. This paper makes the following contributions:
-
A language and type system with extensible signatures for datasort refinements (Sect. 3). Refinements are extended by blocks that are checked to ensure that they do not weaken a sort’s inversion principle, which would make typing unsound.
-
A new formulation of typing (Sect. 4) for case expressions. This formulation is based on a notion of finding the intersection of a type with a pattern; it concisely models the interesting aspects of realistic ML-style patterns.
-
Type (datasort) preservation and progress for the type assignment system, stated in Sect. 6 and proved in Appendix B, with respect to a standard call-by-value operational semantics (Sect. 5).
-
A bidirectional type system (Sect. 7), which directly yields an algorithm. We prove that this system is sound (given a bidirectional typing derivation, erasing annotations yields a type assignment derivation) and complete (given any type assignment derivation, annotations can be added to make bidirectional typing succeed).
The appendix, which includes definitions and proofs omitted for space reasons, can be found at http://www.cs.queensu.ca/~jana/papers/extensible.
2 Datasort Refinements
What are Datasort Refinements? Datasort refinements are a syntactic discipline for enforcing invariants. This is a play on Reynolds’s definition of types as a “syntactic discipline for enforcing levels of abstraction” (Reynolds 1983). Datasorts allow programmers to conveniently categorize inductive data, and operations on such data, more precisely than in conventional type systems.
Indexed types and related systems (e.g. liquid types and other “refinement types”) also serve that purpose, but datasorts are highly syntactic, whereas indexed types depend on the semantics of a constraint domain. For example, to check the safety of accessing the element at position  of a 0-based array of length
of a 0-based array of length  , an indexed type system must check whether the proposition
, an indexed type system must check whether the proposition  is entailed in the theory of integers (under some set of assumptions, e.g.
is entailed in the theory of integers (under some set of assumptions, e.g.  ). The truth of
). The truth of  depends on the semantics of arithmetic, whereas membership in a datasort only depends on a head constructor and the datasorts of its arguments. Put roughly, datasorts express regular grammars, and indexed types express grammars with more powerful side conditions. (Unrestricted dependent types can express arbitrarily precise side conditions.)
depends on the semantics of arithmetic, whereas membership in a datasort only depends on a head constructor and the datasorts of its arguments. Put roughly, datasorts express regular grammars, and indexed types express grammars with more powerful side conditions. (Unrestricted dependent types can express arbitrarily precise side conditions.)
Applications of Datasort Refinements. Datasorts are especially suited to applications of symbolic computing, such as compilers and theorem provers. Compilers usually work with multiple internal languages, from abstract syntax through to intermediate languages. These internal languages may be decomposed into further variants: source ASTs with and without syntactic sugar, A-normal form, and so on. Similarly, theorem provers, SMT solvers, and related tools transform formulas into various normal forms or sublanguages: quantifier-free Boolean formulas, conjunctive normal form, formulas with no free variables, etc. Many such invariants can be expressed by regular tree grammars, and hence by datasorts.
Our extensible refinements offer the ability to use new refinements of a datatype when the need arises, without the need to update a global refinement declaration. For example, we could extend the types in Fig. 1, in which \(\mathsf {clause}\) contains disjunctions of literals and \(\mathsf {cnf}\) contains conjunctions of clauses, with a new sort for conjunctions of literals:

What are Datasort Refinements Not? First, datasorts are not really types, at least not in the sense of Hindley–Milner type systems. A function on bitstrings (Sect. 1) has a best, or principal, type:  . In contrast, such a function may have many refined types (sometimes called sorts), depending not only on the way the programmer chose to refine the \(\mathsf {bits}\) type, but on which possible properties they wish to check. The type, or sort, of a function is a tiny module interface. In a conventional Hindley–Milner type system, there is a best interface (the principal type); with datasorts, the “best” interface is—as with a module interface, which may reveal different aspects of the module—the one the programmer thinks best. Maybe the programmer only cares that the function preserves odd parity, and annotates it with
. In contrast, such a function may have many refined types (sometimes called sorts), depending not only on the way the programmer chose to refine the \(\mathsf {bits}\) type, but on which possible properties they wish to check. The type, or sort, of a function is a tiny module interface. In a conventional Hindley–Milner type system, there is a best interface (the principal type); with datasorts, the “best” interface is—as with a module interface, which may reveal different aspects of the module—the one the programmer thinks best. Maybe the programmer only cares that the function preserves odd parity, and annotates it with  ; the compiler will reject calls with \(\mathsf {even}\) bitstrings, even though such a call would be conventionally well-typed.
; the compiler will reject calls with \(\mathsf {even}\) bitstrings, even though such a call would be conventionally well-typed.
To infer sorts, as in the original work of Freeman, is like assuming that all declarations in a module should be exposed. (Tools that suggest possible invariants could be useful, just as a tool that suggests possible module interfaces could be useful. But such tools are not the focus of this paper.)
3 A Type System with Extensible Refinements
This section gives our language’s syntax, introduces signatures, discusses the introduction and elimination forms for datasorts, and presents the typing rules. The details of typing pattern matching are in Sect. 4.
3.1 Syntax
The syntax of expressions (Fig. 2) includes functions  , function application
, function application  , pairs
, pairs  , constructors
, constructors  , and case expressions. Signatures are extended by
, and case expressions. Signatures are extended by  .
.
Types (Fig. 3), written  and
and  , include unit (
, include unit ( ), function, and product types, along with datasorts
), function, and product types, along with datasorts  and
and  . The intersection type
. The intersection type  represents the conjunction of the two properties denoted by
represents the conjunction of the two properties denoted by  and
and  ; for example, a function to repeat a bitstring could be checked against type
; for example, a function to repeat a bitstring could be checked against type  : given any bitstring
: given any bitstring  , the repetition
, the repetition  has even parity.
has even parity.
3.2 Unrefined Types and Signatures
Our unrefined types  , in Fig. 4, are very simple: unit
, in Fig. 4, are very simple: unit  , functions
, functions  , products
, products  , and datatypes
, and datatypes  . We assume that each datatype has a known set of constructors: for example, the bitstring type of Sect. 1 has constructors \(\mathsf {Empty}\), \(\mathsf {One}\) and \(\mathsf {Zero}\). Refinements don’t add constructors; they only refine the types of the given constructors. We assume that each program has some unrefined signature
. We assume that each datatype has a known set of constructors: for example, the bitstring type of Sect. 1 has constructors \(\mathsf {Empty}\), \(\mathsf {One}\) and \(\mathsf {Zero}\). Refinements don’t add constructors; they only refine the types of the given constructors. We assume that each program has some unrefined signature  that gives datatype names (
that gives datatype names ( ) and (unrefined) constructor typings (
) and (unrefined) constructor typings ( ). Since this signature is the same throughout a program, we elide it in most judgment forms.
). Since this signature is the same throughout a program, we elide it in most judgment forms.
The judgment  says that
says that  is a refinement of
is a refinement of  . Both the symbol
. Both the symbol  and several of the rules are reminiscent of subtyping, but that is misleading: sorts and types are not in an inclusion relation in the sense of subtyping, because the rule for
and several of the rules are reminiscent of subtyping, but that is misleading: sorts and types are not in an inclusion relation in the sense of subtyping, because the rule for  is covariant, not contravariant. Covariance is needed for functions whose domains are nontrivially refined, e.g.
is covariant, not contravariant. Covariance is needed for functions whose domains are nontrivially refined, e.g.  , which is not a subtype of
, which is not a subtype of  because
because  .
.
Rule  implements the usual refinement restriction: both parts of an intersection
implements the usual refinement restriction: both parts of an intersection  must refine the same unrefined type
must refine the same unrefined type  .
.
3.3 Signatures
Refinements are defined by signatures  (Fig. 4).
(Fig. 4).
As in past datasort systems, we separate signatures  from typing contexts
from typing contexts  . Typing assumptions over term variables (
. Typing assumptions over term variables ( ,
,  , etc.) in
, etc.) in  can mention sorts declared in
can mention sorts declared in  , but the signature
, but the signature  cannot mention the term variables declared in
cannot mention the term variables declared in  . Thus, our judgment for term typing will have the form
. Thus, our judgment for term typing will have the form  , where the term
, where the term  can include constructors declared in
can include constructors declared in  and variables declared in
and variables declared in  , and the type
, and the type  can include sorts declared in
can include sorts declared in  . Some judgments, like subsorting
. Some judgments, like subsorting  and subtyping
and subtyping  , are independent of variable typing and don’t include
, are independent of variable typing and don’t include  at all.
at all.
Traditional formulations of refinements assume the signature is given once at the beginning of the program. Since the same signature is used throughout a given typing derivation, the signature can be omitted from the typing judgments. In this paper, our goal is to support extensible refinements, where the signature can evolve within a typing derivation; in this respect, the signature is analogous to an ordinary typing context  , which is extended in subderivations that type
, which is extended in subderivations that type  -expressions and other binding forms. So the signature must be explicit in our judgment forms (Fig. 5).
-expressions and other binding forms. So the signature must be explicit in our judgment forms (Fig. 5).
Constructor types  are types of the form
are types of the form  . In past formulations of datasorts, constructor types in the signature use intersection to represent multiple behaviours. For example, a “one” constructor for bitstrings, which represents appending a 1 bit, takes odd-parity bitstrings to even-parity and vice versa; its type in the signature is the intersection type
. In past formulations of datasorts, constructor types in the signature use intersection to represent multiple behaviours. For example, a “one” constructor for bitstrings, which represents appending a 1 bit, takes odd-parity bitstrings to even-parity and vice versa; its type in the signature is the intersection type  . Such a formulation ensures that the signature has a standard property of (typing) contexts: each data constructor is declared only once; additional behaviours are conjoined (intersected) within a single declaration
. Such a formulation ensures that the signature has a standard property of (typing) contexts: each data constructor is declared only once; additional behaviours are conjoined (intersected) within a single declaration  . In our setting, we must be careful about not only which types a constructor has, but when those types were declared. The reasons are explained below; for now, just note that we will write something like
. In our setting, we must be careful about not only which types a constructor has, but when those types were declared. The reasons are explained below; for now, just note that we will write something like  rather than
rather than  .
.
Structure of Signatures. A signature  is a sequence of blocks
is a sequence of blocks  of declarations, where refinements declared in outer scopes in the program appear to the left of those declared in inner scopes.
of declarations, where refinements declared in outer scopes in the program appear to the left of those declared in inner scopes.
Writing  declares
declares  to be a sort refining some (unrefined) datatype
to be a sort refining some (unrefined) datatype  ; however, we usually elide the datatype and write just
; however, we usually elide the datatype and write just  . The declarations
. The declarations  , called the block of
, called the block of  , define the values (constructors) of
, define the values (constructors) of  , and the subsortings for
, and the subsortings for  . Declarations outside this block may declare new subsorts and supersorts of
. Declarations outside this block may declare new subsorts and supersorts of  only if doing so would not affect
only if doing so would not affect  —for example, adding inhabitants to
—for example, adding inhabitants to  via a constructor declaration, or declaring a new subsorting between
via a constructor declaration, or declaring a new subsorting between  and previously declared sorts, would affect
and previously declared sorts, would affect  and will be forbidden (via signature well-formedness). The grammar generalizes this construct to multiple sorts, e.g.
and will be forbidden (via signature well-formedness). The grammar generalizes this construct to multiple sorts, e.g.  , abbreviated as
, abbreviated as  .
.
Writing  says that
says that  is a subsort of
is a subsort of  , and
, and  says that constructor
says that constructor  has type
has type  , where
, where  has the form
has the form  . A constructor
. A constructor  can be given more than one type:
can be given more than one type:  .
.
Adding inhabitants to a sort is only allowed within its block. Thus, the following signature is ill-formed, because  adds the value
adds the value  to
to  , but
, but  is not within
is not within  ’s block:
’s block:  . New sorts can be declared as subsorts and supersorts of each other, and of previously declared sorts:
. New sorts can be declared as subsorts and supersorts of each other, and of previously declared sorts:  .
.
However, a block cannot modify the subsorting relation between earlier sorts; “backpatching”  into the first block, through a new intermediate sort
into the first block, through a new intermediate sort  , is not permitted: The signature
, is not permitted: The signature  is not permitted even though it looks safe: sorts
is not permitted even though it looks safe: sorts  and
and  have the same set of inhabitants—the singleton set
have the same set of inhabitants—the singleton set  —so the values of
—so the values of  are a subset of the values of
are a subset of the values of  . But this fact was not declared in the first block, which is the definition of
. But this fact was not declared in the first block, which is the definition of  and
and  . We assume the declaration of the first block completely reflects the programmer’s intent: if they had wanted structural subsorting, rather than nominal subsorting, they should have declared
. We assume the declaration of the first block completely reflects the programmer’s intent: if they had wanted structural subsorting, rather than nominal subsorting, they should have declared  in the first block. Allowing backpatching would not violate soundness, but would reduce the power of the type system: nominal subsorting would no longer be supported, since it could be made structural after the fact.
in the first block. Allowing backpatching would not violate soundness, but would reduce the power of the type system: nominal subsorting would no longer be supported, since it could be made structural after the fact.
Ordering. A block  can refer to the sorts
can refer to the sorts  being defined and to sorts declared to the left. In contrast to block ordering, the order of declarations inside a block doesn’t matter.
being defined and to sorts declared to the left. In contrast to block ordering, the order of declarations inside a block doesn’t matter.
3.4 Introduction Form
From a type-theoretic perspective, the first questions about a type are: (1) How are the type’s inhabitants created? That is, what are the type’s introduction rules? (2) How are its inhabitants used? That is, what are its elimination rules? (Gentzen (1934) would ask the questions in this order; the reverse order has been considered by Dummett, among others (Zeilberger 2009).) In our setting, we must also ask: What happens with the introduction and elimination forms when new refinements are introduced?
In the introduction rule—\(\mathsf {DataI~}\)in Fig. 6—the signature  is separated from the ordinary context
is separated from the ordinary context  (which contains typing assumptions of the form
(which contains typing assumptions of the form  ). The typing of
). The typing of  is delegated to its first premise,
is delegated to its first premise,  , so we need a way to derive this judgment. At the top of Fig. 6, we define a single rule \(\mathsf {ConArr}\), which looks up the constructor in the signature and weakens the result type (codomain), expressing a subsumption principle. (Since we’ll have subsumption as a typing rule, including it here is an unforced choice; its presence is meant to make the metatheory of constructor typing go more smoothly.)
, so we need a way to derive this judgment. At the top of Fig. 6, we define a single rule \(\mathsf {ConArr}\), which looks up the constructor in the signature and weakens the result type (codomain), expressing a subsumption principle. (Since we’ll have subsumption as a typing rule, including it here is an unforced choice; its presence is meant to make the metatheory of constructor typing go more smoothly.)
In a system of extensible refinements, adding refinements to a signature should preserve typing. That is, if  , then
, then  . This is a weakening property: we can derive, from the judgment that
. This is a weakening property: we can derive, from the judgment that  has type
has type  under
under  , the logically weaker judgment that
, the logically weaker judgment that  has type
has type  under more assumptions
under more assumptions  . (The signature becomes longer, therefore stronger; but a turnstile is a kind of implication with the signature as antecedent, so the judgment becomes weaker, hence “weakening”.) So for the introduction form, we need that if
. (The signature becomes longer, therefore stronger; but a turnstile is a kind of implication with the signature as antecedent, so the judgment becomes weaker, hence “weakening”.) So for the introduction form, we need that if  , then
, then  . Under our formulation of the signature, this holds: If
. Under our formulation of the signature, this holds: If  , then there exists
, then there exists  such that
such that  . Therefore, there exists
. Therefore, there exists  . Likewise, since
. Likewise, since  , we also have
, we also have  . One cannot use
. One cannot use  to withdraw a commitment made in
to withdraw a commitment made in  .Footnote 2
.Footnote 2
3.5 Elimination Form: Case Expressions
Exhaustiveness checking for case expressions assumes complete knowledge about the inhabitants of types. Thus, we must avoid extending a signature in a way that adds inhabitants to previously declared sorts. Consider the case expression  which is exhaustive for the signature
which is exhaustive for the signature  but not for
but not for

Suppose we type-check the case expression under  , but then extend
, but then extend  to
to  . Evaluating the above case expression with
. Evaluating the above case expression with  will “fall off the end”. The inversion principle that “every \(\mathsf {empty}\) has the form
will “fall off the end”. The inversion principle that “every \(\mathsf {empty}\) has the form  ” is valid under
” is valid under  , but with the additional type for \(\mathsf {Cons}\) in
, but with the additional type for \(\mathsf {Cons}\) in  , that inversion principle becomes invalid under
, that inversion principle becomes invalid under  . Our system will reject the latter signature as ill-formed.
. Our system will reject the latter signature as ill-formed.
In the following, “up” and “down” are used in the usual sense: a subsort is below its supersort. In  , the second constructor type for \(\mathsf {Cons}\) had a smaller codomain than the first: the second type had \(\mathsf {empty}\), instead of \(\mathsf {list}\). Varying the codomain downward can be sound when the lower codomain is newly defined:
, the second constructor type for \(\mathsf {Cons}\) had a smaller codomain than the first: the second type had \(\mathsf {empty}\), instead of \(\mathsf {list}\). Varying the codomain downward can be sound when the lower codomain is newly defined:  . Here, the inversion principle that every \(\mathsf {empty}\) is \(\mathsf {Nil}\) is still valid (along with the new inversion principle that every \(\mathsf {subempty}\) is \(\mathsf {Nil}\)). We only added information about a new sort \(\mathsf {subempty}\), without changing the definition of \(\mathsf {list}\) and \(\mathsf {empty}\).
. Here, the inversion principle that every \(\mathsf {empty}\) is \(\mathsf {Nil}\) is still valid (along with the new inversion principle that every \(\mathsf {subempty}\) is \(\mathsf {Nil}\)). We only added information about a new sort \(\mathsf {subempty}\), without changing the definition of \(\mathsf {list}\) and \(\mathsf {empty}\).
Moving the Domain Down. Giving a new type whose domain is smaller, but that has the same codomain, is sound but pointless. For example, extending  with
with  , which is the same as the type
, which is the same as the type  has for
has for  except that the domain is \(\mathsf {empty}\) instead of \(\mathsf {list}\), is sound. The inversion principle for values
except that the domain is \(\mathsf {empty}\) instead of \(\mathsf {list}\), is sound. The inversion principle for values  of type \(\mathsf {list}\) in
of type \(\mathsf {list}\) in  alone is “either (1)
alone is “either (1)  has the form
has the form  , or (2)
, or (2)  has the form
has the form  where
where  has type \(\mathsf {list}\)”. Reading off the new inversion principle for \(\mathsf {list}\) from
has type \(\mathsf {list}\)”. Reading off the new inversion principle for \(\mathsf {list}\) from  , we get “either (1)
, we get “either (1)  has the form
has the form  , or (2)
, or (2)  has the form
has the form  where
where  has type \(\mathsf {list}\), or (3)
has type \(\mathsf {list}\), or (3)  has the form
has the form  where
where  has type \(\mathsf {empty}\)”. Since \(\mathsf {empty}\) is a subsort of \(\mathsf {list}\), part (3) implies part (2), and any case arm that checks under the assumption that
has type \(\mathsf {empty}\)”. Since \(\mathsf {empty}\) is a subsort of \(\mathsf {list}\), part (3) implies part (2), and any case arm that checks under the assumption that  must also check under the assumption that
must also check under the assumption that  . Here, the new signature is equivalent to
. Here, the new signature is equivalent to  alone; the “new” type for \(\mathsf {Cons}\) is spurious.
alone; the “new” type for \(\mathsf {Cons}\) is spurious.
Moving the Codomain Up. Symmetrically, giving a new type whose codomain gets larger is sound but pointless. For example, adding  to
to  has no effect, because (in the introduction form) we could use the old type
has no effect, because (in the introduction form) we could use the old type  with subsumption (
with subsumption ( ).
).
Moving the Domain Up. Making the domain of a constructor larger is unsound in general. To show this, we need a different starting signature  .
.

This isn’t a very useful signature—it doesn’t allow construction of any list with more than one element—but it is illustrative. We can read off from  the following inversion principle for values
the following inversion principle for values  of sort \(\mathsf {nonempty}\): “
of sort \(\mathsf {nonempty}\): “ has the form
has the form  where
where  has type \(\mathsf {empty}\)”. If
has type \(\mathsf {empty}\)”. If  then
then  is exhaustive under
is exhaustive under  . Now, extend
. Now, extend  :
:  . For the signature
. For the signature  , the inversion principle for \(\mathsf {nonempty}\) should be “(1)
, the inversion principle for \(\mathsf {nonempty}\) should be “(1)  has the form
has the form  where
where  has type \(\mathsf {empty}\), or (2)
has type \(\mathsf {empty}\), or (2)  has the form
has the form  where
where  has type \(\mathsf {list}\)”. But there are more values of type \(\mathsf {list}\) than of type \(\mathsf {empty}\). The new inversion principle gives less precise information about the argument
has type \(\mathsf {list}\)”. But there are more values of type \(\mathsf {list}\) than of type \(\mathsf {empty}\). The new inversion principle gives less precise information about the argument  , meaning that the old inversion principle gives more precise information than
, meaning that the old inversion principle gives more precise information than  allows. Concretely, the case expression above was exhaustive under
allows. Concretely, the case expression above was exhaustive under  , but is not exhaustive under
, but is not exhaustive under  because
because  has type
has type  .
.
The above examples show that signature extension can be sound but useless, unsound, or sound and useful (when the domain and codomain, or just the codomain, are moved down). Ruling out unsoundness will be the main purpose of our type system, where unsoundness includes raising a “match” exception due to a nonexhaustive case. The critical requirement is that each block must not affect previously declared sorts by adding constructors to them, or by adding subsortings between them.
3.6 Typing
Figure 6 gives rules deriving the main typing judgment  . The variable rule
. The variable rule  , the introduction (
, the introduction ( ) and elimination (
) and elimination ( ) rules for
) rules for  , and the introduction rules for the unit type (
, and the introduction rules for the unit type ( ) and products (
) and products ( ) are standard. Products can be eliminated via
) are standard. Products can be eliminated via  , so they need no elimination rule.
, so they need no elimination rule.
Subsumption. A subsumption rule  incorporates subtyping, based on the subsort relation
incorporates subtyping, based on the subsort relation  ; see Sect. 3.7. Several of the subtyping rules express the same properties as elimination rules would; for example, anything of type
; see Sect. 3.7. Several of the subtyping rules express the same properties as elimination rules would; for example, anything of type  has type
has type  and also type
and also type  . Consequently, we can omit these elimination rules without losing expressive power.
. Consequently, we can omit these elimination rules without losing expressive power.
Intersection. The introduction rule  corresponds to a binary version of the introduction rule for parametric polymorphism in System F. The restriction to a value
corresponds to a binary version of the introduction rule for parametric polymorphism in System F. The restriction to a value  avoids unsoundness in the presence of mutable references (Davies and Pfenning 2000), similar to SML’s value restriction for parametric polymorphism (Wright 1995). We omit the elimination rules, which are admissible using
avoids unsoundness in the presence of mutable references (Davies and Pfenning 2000), similar to SML’s value restriction for parametric polymorphism (Wright 1995). We omit the elimination rules, which are admissible using  and subtyping (Sect. 3.7).
and subtyping (Sect. 3.7).

Datasorts. Rule  introduces a datasort, according to a constructor type found in
introduces a datasort, according to a constructor type found in  (via the
(via the  judgment). Rule
judgment). Rule  examines an expression
examines an expression  of type
of type  and checks matches
and checks matches  under the assumption that the expression matches the wildcard pattern
under the assumption that the expression matches the wildcard pattern  ; see Sect. 4.
; see Sect. 4.
Re-refinement. Rule  allows sorts to be declared. Its premises check that (1) the signature
allows sorts to be declared. Its premises check that (1) the signature  is a valid extension of
is a valid extension of  (see Sect. 3.8); (2) the type
(see Sect. 3.8); (2) the type  of the expression is well-formed without the extension
of the expression is well-formed without the extension  , which prevents sorts declared in
, which prevents sorts declared in  from escaping their scope; (3) that the expression
from escaping their scope; (3) that the expression  is well-typed under the extended signature
is well-typed under the extended signature  .
.
3.7 Subtyping
Our subtyping judgment  says that all values of type
says that all values of type  also have type
also have type  . The rules follow the style of Dunfield and Pfenning
(2003); in particular, the rules are orthogonal (each rule mentions only one kind of connective) and transitivity is admissible. Instead of an explicit transitivity rule, we bake transitivity into each rule; for example, rule
. The rules follow the style of Dunfield and Pfenning
(2003); in particular, the rules are orthogonal (each rule mentions only one kind of connective) and transitivity is admissible. Instead of an explicit transitivity rule, we bake transitivity into each rule; for example, rule  has a premise
has a premise  and conclusion
and conclusion  , rather than just
, rather than just  (with no premises). This makes the rules easier to implement: to decide whether
(with no premises). This makes the rules easier to implement: to decide whether  , we never have to guess a middle type
, we never have to guess a middle type  such that
such that  and
and  (Fig. 7).
(Fig. 7).
3.8 Signature Well-Formedness
A signature is well-formed if standard conditions (e.g. no duplicate declarations of sorts) and conservation conditions hold. Reading Fig. 8 from bottom to top, we start with well-formedness of signatures  . For each block
. For each block  , rule
, rule  checks that the sorts
checks that the sorts  are not duplicates (
are not duplicates ( ), and then checks that (1) subsorting is conserved by
), and then checks that (1) subsorting is conserved by  and (2) each element in
and (2) each element in  is safe.
is safe.
(1) Subsorting Preservation. The subsortings declared in  must not affect the subsort relation between sorts previously declared in
must not affect the subsort relation between sorts previously declared in  . The left-to-right direction of this “iff” always holds by weakening: adding to a signature cannot delete edges in the subsort relation. The right-to-left direction is contingent on the contents of
. The left-to-right direction of this “iff” always holds by weakening: adding to a signature cannot delete edges in the subsort relation. The right-to-left direction is contingent on the contents of  ; see signature
; see signature  in Sect. 3.3. This premise could also be written as
in Sect. 3.3. This premise could also be written as  , where
, where  is the
is the  relation restricted to sorts in
relation restricted to sorts in  .
.
(2a) Subsort Elements. Rule  checks that the subsorts are in scope.
checks that the subsorts are in scope.
(2b) Constructor Element Safety. Rule BlockCon’s first premise checks that  . (Certain declarations with
. (Certain declarations with  would be safe, but useless.) Its second premise checks that the constructor type
would be safe, but useless.) Its second premise checks that the constructor type  is well-formed. Finally, for all sorts
is well-formed. Finally, for all sorts  that were (1) previously declared (in
that were (1) previously declared (in  ) and (2) supersorts of the constructor’s codomain (
) and (2) supersorts of the constructor’s codomain ( ), the rule checks that the constructor is “safe at
), the rule checks that the constructor is “safe at  ”.
”.
The judgment  says that adding the constructor typing
says that adding the constructor typing  does not invalidate
does not invalidate  ’s inversion principle for
’s inversion principle for  . Rule
. Rule  checks that signature
checks that signature  already has a constructor typing
already has a constructor typing  , where
, where  , such that
, such that  . Thus, any value
. Thus, any value  typed using
typed using  can already be typed using
can already be typed using  , which is a subsort of
, which is a subsort of  , so the new constructor typing
, so the new constructor typing  does not add inhabitants to
does not add inhabitants to  .
.
This check is not analogous to function subtyping, because we need covariance ( ), not contravariance. The relation
), not contravariance. The relation  (Fig. 4) is a closer analogy.
(Fig. 4) is a closer analogy.
More subtly,  also checks that
also checks that  . Suppose we have the signature
. Suppose we have the signature  and extend it with
and extend it with  . (To focus on the issue at hand, we assume
. (To focus on the issue at hand, we assume  and
and  take no arguments.) For the original signature
take no arguments.) For the original signature  , the inversion principle for
, the inversion principle for  is: If a value
is: If a value  has type
has type  , then either
, then either  and
and  has type
has type  , or
, or  and
and  has type
has type  . However, under the extended signature, there is a new possibility:
. However, under the extended signature, there is a new possibility:  has type
has type  . Merely being inhabited by
. Merely being inhabited by  is not sufficient to allow
is not sufficient to allow  to be a subsort of
to be a subsort of  .
.
If, instead, we start with  then the inversion principle for
then the inversion principle for  under
under  is that
is that  has type
has type  , type
, type  , or type
, or type  . Therefore, any case arm whose pattern is
. Therefore, any case arm whose pattern is  must be checked assuming
must be checked assuming  . If an expression can be typed assuming
. If an expression can be typed assuming  , then it can be typed assuming
, then it can be typed assuming  for any
for any  , so the inversion principle (again, under
, so the inversion principle (again, under  before extension) is equivalent to “
before extension) is equivalent to “ has type
has type  ”. Extending
”. Extending  with
with  would extend the inversion principle to say “if
would extend the inversion principle to say “if  then
then  has type
has type  , or
, or  has type
has type  ”, but since
”, but since  the extended inversion principle is equivalent to that for
the extended inversion principle is equivalent to that for  under
under  .
.
The  premise of
premise of  is needed to prove the constructor lemma (Lemma 12), which says that a constructor typing in an extended signature must be below a constructor typing in the original signature.
is needed to prove the constructor lemma (Lemma 12), which says that a constructor typing in an extended signature must be below a constructor typing in the original signature.
4 Typing Pattern Matching
Pattern matching is how a program gives different answers on different inputs. A key motivation for datasort refinements is to exclude impossible patterns, so that programmers can avoid having to choose between writing impossible case arms (that raise an “impossible” exception) and ignoring nonexhaustiveness warnings. The pattern typing rules must model the relationship between datasorts and the operational semantics of pattern matching. It’s no surprise, then, that in datasort refinement systems, case expressions lead to the most interesting typing rules.
The relationship between types and patterns is more involved than with, say, Damas–Milner plus inductive datatypes: with (unrefined) inductive datatypes, all the information needed to check for exhaustiveness (also called coverage) is immediately available as soon as the type of the scrutinee is known. Moreover, types for pattern variables can be “read off” by traversing the pattern top-down, tracking the definition of the scrutinee’s inductive datatype. But with datasorts, a set of patterns that looks nonexhaustive at first glance—looking only at the head constructors—may in fact be exhaustive, thanks to the inner patterns.
Giving types to pattern variables is also tricky, because sufficiently precise types may be evident only after examining the whole pattern. For example, when matching  against the pattern
against the pattern  , we shouldn’t settle on
, we shouldn’t settle on  because the scrutinee
because the scrutinee  has type
has type  ; we should descend into the pattern and observe that
; we should descend into the pattern and observe that  and
and  , so
, so  must have type
must have type  .
.
Restricting the form of case expressions to a single layer of clearly disjoint patterns  would simplify the rules, at the cost of a big gap between theory and practice: Since real implementations need to support nested patterns, the theory fails to model the real complexities of exhaustiveness checking and pattern variable typing. Giving code examples becomes fraught; either we flatten case expressions (resulting in code explosion), or we handwave a lot.
would simplify the rules, at the cost of a big gap between theory and practice: Since real implementations need to support nested patterns, the theory fails to model the real complexities of exhaustiveness checking and pattern variable typing. Giving code examples becomes fraught; either we flatten case expressions (resulting in code explosion), or we handwave a lot.
Another option is to support the full syntax of case expressions, except for as-patterns, so that pattern variables occur only at the leaves. If subsorting were always structural, as in Davies’s system, we could exploit a handy equivalence between patterns and values: if the pattern is  , let-bind
, let-bind  to
to  inside the case arm, letting rule
inside the case arm, letting rule  figure out the type of
figure out the type of  . But with nominal subsorting, constructing a value is not equivalent; see Davies
(2005, pp. 234–235) and Dunfield
(2007b, pp. 112–113).
. But with nominal subsorting, constructing a value is not equivalent; see Davies
(2005, pp. 234–235) and Dunfield
(2007b, pp. 112–113).
Our approach is to support the full syntax, including as-patterns. This approach was taken by Dunfield (2007b, Chap. 4), but our system seems simpler—partly because (except for signature extension) our type system omits indexed types and union types, but also because we avoid embedding typing derivations inside derivations of pattern typing.
Instead, we confine most of the complexity to a single mechanism: a function called  , which returns a set of types (and contexts that type
, which returns a set of types (and contexts that type  -variables) that represent the intersection between a type and a pattern. The definition of this function is not trivial, but does not refer to expression-level typing.
-variables) that represent the intersection between a type and a pattern. The definition of this function is not trivial, but does not refer to expression-level typing.
4.1 Unrefined Pattern Typing, Match Typing, and Pattern Operations
Figure 9 defines a judgment  that says that pattern
that says that pattern  matches values of unrefined type
matches values of unrefined type  under the unrefined signature
under the unrefined signature  .
.
Rule  for case expressions (Fig. 6) invokes a match typing judgment,
for case expressions (Fig. 6) invokes a match typing judgment,  . In this judgment,
. In this judgment,  is a residual pattern that represents the space of possible values. For the first arm in a case expression, no patterns have yet failed to match, so the residual pattern in the premise of
is a residual pattern that represents the space of possible values. For the first arm in a case expression, no patterns have yet failed to match, so the residual pattern in the premise of  is
is  .
.
Each arm, of the form  , is checked by rule
, is checked by rule  (Fig. 10). The leftmost premises check that the type
(Fig. 10). The leftmost premises check that the type  corresponds to the pattern type
corresponds to the pattern type  . The middle “for all” checks
. The middle “for all” checks  under various assumptions produced by the
under various assumptions produced by the  function (Sect. 4.2) with respect to the pattern
function (Sect. 4.2) with respect to the pattern  , ensuring that if
, ensuring that if  matches the value at run time, the arm is well-typed. The last premise moves on to the remaining matches; there, we know that the value did not match
matches the value at run time, the arm is well-typed. The last premise moves on to the remaining matches; there, we know that the value did not match  , so we subtract
, so we subtract  from the previous residual pattern
from the previous residual pattern  —expressed as
—expressed as  . These operations are defined in the appendix (Fig. 13).
. These operations are defined in the appendix (Fig. 13).
When typing reaches the end of the matches,  in rule
in rule  , we check that the case expression is exhaustive by checking that
, we check that the case expression is exhaustive by checking that  returns
returns  . For case expressions that are syntactically exhaustive, such as a case expression over lists that has both \(\mathsf {Nil}\) and \(\mathsf {Cons}\) arms, the residual pattern
. For case expressions that are syntactically exhaustive, such as a case expression over lists that has both \(\mathsf {Nil}\) and \(\mathsf {Cons}\) arms, the residual pattern  will be the empty pattern
will be the empty pattern  ; the
; the  function on an empty pattern returns \(\emptyset \).
function on an empty pattern returns \(\emptyset \).
We define pattern complement  and pattern intersection
and pattern intersection  in the appendix (Fig. 13). For example,
in the appendix (Fig. 13). For example,  . No types appear in these definitions, but the complement of a constructor pattern
. No types appear in these definitions, but the complement of a constructor pattern  uses the (implicit) unrefined signature
uses the (implicit) unrefined signature  . Our definition of pattern complement never generates
. Our definition of pattern complement never generates  -patterns, so we need not define intersection for
-patterns, so we need not define intersection for  -patterns.
-patterns.
4.2 The intersect function
We define a function \(\mathsf {intersect}\) that builds the “intersection” of a type and a pattern. Given a signature  , type
, type  and pattern
and pattern  , the \(\mathsf {intersect}\) function returns a (possibly empty) set of tracks
, the \(\mathsf {intersect}\) function returns a (possibly empty) set of tracks  . Each track
. Each track  has a list of typings
has a list of typings  (giving the types of
(giving the types of  -variables) and a type
-variables) and a type  that represents the subset of values inhabiting
that represents the subset of values inhabiting  that also match
that also match  . The union of
. The union of  through
through  constitutes the intersection of
constitutes the intersection of  and
and  . We call these “tracks” because each one represents a possible shape of the values that match p, and the type-checking “train” must check a given case arm under each track’s
. We call these “tracks” because each one represents a possible shape of the values that match p, and the type-checking “train” must check a given case arm under each track’s  .
.
Many of the clauses in the definition of \(\mathsf {intersect}\) (see Fig. 10) are straightforward. The intersection of  with the wildcard \({\_\!\_}\) is just
with the wildcard \({\_\!\_}\) is just  . Dually, the intersection of
. Dually, the intersection of  with the empty pattern
with the empty pattern  is the empty set. In the same vein, the intersection of
is the empty set. In the same vein, the intersection of  with the or-pattern
with the or-pattern  is the union of two intersections (
is the union of two intersections ( with
with  , and
, and  with
with  ). The intersection of a product
). The intersection of a product  with a pair pattern is the union of products of the pointwise intersections.
with a pair pattern is the union of products of the pointwise intersections.
The most interesting case is when we intersect a sort  with a pattern of the form
with a pattern of the form  . For this case,
. For this case,  iterates through all the constructor declarations in
iterates through all the constructor declarations in  that could have been used to create the given value: those of the form
that could have been used to create the given value: those of the form  where
where  . For each such declaration, it calls
. For each such declaration, it calls  on
on  and
and  . For each resulting track
. For each resulting track  , it returns a track
, it returns a track  .
.
Optimization. In practice, it may be necessary to optimize the result of  . If
. If  then
then  returns
returns  . Since any case arm that checks under
. Since any case arm that checks under  will check under
will check under  , there is no point in trying to check under
, there is no point in trying to check under  . Instead, we should check only under
. Instead, we should check only under  . A similar optimization in the Stardust type checker could reduce the size of the set of tracks by “about an order of magnitude” Dunfield
(2007b, p.112).
. A similar optimization in the Stardust type checker could reduce the size of the set of tracks by “about an order of magnitude” Dunfield
(2007b, p.112).
Missing Clauses? As is standard in typed languages, pattern matching doesn’t look inside  , so
, so  needs no clause for
needs no clause for  /
/ . If we can’t match on an arrow type, we don’t need to match on intersections of arrows. The other useful case of intersection is on sorts,
. If we can’t match on an arrow type, we don’t need to match on intersections of arrows. The other useful case of intersection is on sorts,  . However, an intersection of sorts can be obtained by declaring a new sort below
. However, an intersection of sorts can be obtained by declaring a new sort below  and
and  with the appropriate constructor typings, so we omit such a clause from the definition.
with the appropriate constructor typings, so we omit such a clause from the definition.
Comparison to an Earlier System. A declarative system of rules in Dunfield
(2007b, Chap. 4) appears to be a conservative extension of  : the earlier system supports a richer type system, but for the features in common, the information produced is similar to that of
: the earlier system supports a richer type system, but for the features in common, the information produced is similar to that of  . The earlier system was based on a judgment
. The earlier system was based on a judgment  . To clarify the connection to the present system, we adjust notation; for example, we make
. To clarify the connection to the present system, we adjust notation; for example, we make  explicit.
explicit.
The meta-variables  ,
,  , and
, and  directly correspond to the arguments to
directly correspond to the arguments to  , while
, while  and
and  correspond to
correspond to  and
and  in our rule
in our rule  . No meta-variables correspond directly to the tracks in the result of \(\mathsf {intersect}\), but within
. No meta-variables correspond directly to the tracks in the result of \(\mathsf {intersect}\), but within  , we find subderivations of
, we find subderivations of  , where the set of pairs
, where the set of pairs  indeed correspond to the result of
indeed correspond to the result of  .
.
Cutting through the differences in the formalism, and omitting rules for unions and other features not present in this paper, the earlier system behaves like  . For example,
. For example,  was also handled by considering each component, and assembling all resulting combinations. Perhaps most importantly,
was also handled by considering each component, and assembling all resulting combinations. Perhaps most importantly,  was also handled by considering each constructor type in the signature, filtering out inappropriate codomains, and recursing on
was also handled by considering each constructor type in the signature, filtering out inappropriate codomains, and recursing on  . A rule for
. A rule for  appears in the declarative system in Dunfield
(2007b, Chap. 4), but the rule was never implemented, and seems not to be needed in practice.
appears in the declarative system in Dunfield
(2007b, Chap. 4), but the rule was never implemented, and seems not to be needed in practice.
Since the information given by the older system is precise enough to check interesting invariants of actual programs, our definition of  should also be precise enough.
should also be precise enough.
5 Operational Semantics
We prove our results with respect to a call-by-value, small-step operational semantics. The main judgment form is  , which uses evaluation contexts
, which uses evaluation contexts  . Stepping case expressions is modelled using a judgment
. Stepping case expressions is modelled using a judgment  , which compares each pattern in
, which compares each pattern in  against the value
against the value  being cased upon. This comparison is handled by the judgment
being cased upon. This comparison is handled by the judgment  , which says that
, which says that  is evidence that
is evidence that  matches
matches  (that is,
(that is,  ). The rules are in Fig. 14 in the appendix.
). The rules are in Fig. 14 in the appendix.
6 Metatheory
This section gives definitions, states some lemmas and theorems, and discusses their significance in proving our main results. For space reasons, we summarize a number of lemmas; their full statements appear in the appendix. All proofs are also relegated to the appendix.
Subtyping and Subsorting. Subtyping is reflexive and transitive (Lemmas (Lemmas 6–7). We define what it means for signature extension to preserve subsorting:
Definition 1
(Preserving subsorting). Given  and
and  , we say that
, we say that  preserves subsorting of
preserves subsorting of  iff for all sorts
iff for all sorts  , if
, if  then
then  .
.
This definition allows new sorts in  to be subsorts or supersorts of the old sorts in
to be subsorts or supersorts of the old sorts in  , provided that the subsort relation between the old sorts doesn’t change.
, provided that the subsort relation between the old sorts doesn’t change.
If two signatures do not have subsortings that cross into each other’s domain, they are non-adjacent; non-adjacent signatures preserve subsorting.
Definition 2
(Non-adjacency). Two signatures  and
and  are non-adjacent iff each signature contains no subsortings of the form
are non-adjacent iff each signature contains no subsortings of the form  or
or  , where
, where  and
and  .
.
Theorem 1
(Non-adjacent preservation).
If  preserves subsorting of
preserves subsorting of  and
and  preserves subsorting of
preserves subsorting of 
and  and
and  are non-adjacent then
are non-adjacent then  preserves subsorting of
preserves subsorting of  .
.
Strengthening, Weakening, and Substitution. Theorem 4 (Weakening) will allow the assumptions in a judgment to be changed in two ways: (1) the signature may be strengthened by replacing a signature  with a signature
with a signature  ; and (2) the context may be strengthened by replacing
; and (2) the context may be strengthened by replacing  with a context
with a context  in which any typing assumption
in which any typing assumption  can be replaced with
can be replaced with  , if
, if  .
.
Repeatedly applying (1) with different  leads to a more general notion of strengthening a signature:
leads to a more general notion of strengthening a signature:
Definition 3
A signature  is stronger than
is stronger than  , written
, written  , if
, if  can be obtained from
can be obtained from  by inserting entire signatures at any position in
by inserting entire signatures at any position in  .
.
We often use the less general notion (inserting a single  ), which simplifies proofs. For any result stated less generally, however, the more general strengthening of Definition 3 can be shown by induction on the number of blocks inserted.
), which simplifies proofs. For any result stated less generally, however, the more general strengthening of Definition 3 can be shown by induction on the number of blocks inserted.
Definition 4
Under  , a context
, a context  is stronger than
is stronger than  , written
, written  , if for each
, if for each  , there exists
, there exists  such that
such that  .
.
Several lemmas show weakening. Lemma 8 says that  in
in  can be replaced by a stronger
can be replaced by a stronger  , where
, where  has the form
has the form  or
or  or
or  or
or  or
or  or
or  . Lemma 9 says that
. Lemma 9 says that  can replace
can replace  in
in  .Lemma 10 allows the sort
.Lemma 10 allows the sort  in the judgment
in the judgment  to be replaced by a supersort
to be replaced by a supersort  .
.
Using the above lemmas and Theorem 1, we can show that the key judgment “ ” can be weakened by inserting
” can be weakened by inserting  inside the signature:
inside the signature:
Theorem 2
(Weakening ‘safe’). If  and
and  and
and  and
and  and
and  does not mention anything in
does not mention anything in  and
and  preserves subsorting for
preserves subsorting for  and
and  and
and  then
then  .
.
With this additional lemma, we have weakening for the judgments involved in checking that a signature is well-formed, so we can show that if  is safely extended by
is safely extended by  and separately by
and separately by  , then
, then  and
and  , together, safely extend
, together, safely extend  .
.
Theorem 3
(Signature Interleaving).
If  and
and  and
and  then
then  .
.
Ultimately, we will show type preservation; in the preservation case for the  rule, we extend the signature in a premise. We therefore need to show that the typing judgment can be weakened. Since the typing rules for matches involve the \(\mathsf {intersect}\) function, we need to show that a stronger input to \(\mathsf {intersect}\) yields a stronger output; that is, a longer (stronger) signature yields a stronger type
rule, we extend the signature in a premise. We therefore need to show that the typing judgment can be weakened. Since the typing rules for matches involve the \(\mathsf {intersect}\) function, we need to show that a stronger input to \(\mathsf {intersect}\) yields a stronger output; that is, a longer (stronger) signature yields a stronger type  (a subtype of
(a subtype of  ) and a stronger context
) and a stronger context  typing
typing  -variables.
-variables.
Definition 5
Under a signature  , a track
, a track  is stronger than
is stronger than  , written
, written  , if and only if
, if and only if  and
and  .
.
A set of tracks  is stronger than
is stronger than  , written
, written  , if and only if, for each track
, if and only if, for each track  , there exists a track
, there exists a track  such that
such that  .
.
Lemma 13 says that the result of \(\mathsf {intersect}\) on a stronger signature is stronger. We can then show that weakening holds for the typing judgment itself, along with substitution typing (defined in the appendix) and match typing.
Theorem 4
(Weakening). If  ,
,  ,
,  and
and  then
then
-
(1)
If
 then
then  .
. -
(2)
If
 then
then  .
. -
(3)
If
 then
then  .
.
Properties of Values. Substitution properties (Lemmas 14 and 15) and inversion (or canonical forms) properties (Lemma 16) hold.
Type Preservation and Progress. The last important piece needed for type preservation is that \(\mathsf {intersect}\) does what it says: if a value  matches
matches  , then
, then  has type
has type  where
where  is one of the outputs of \(\mathsf {intersect}\).
is one of the outputs of \(\mathsf {intersect}\).
Theorem 5
(Intersect). If  and
and  and
and  and
and  and
and  then there exists
then there exists  s.t.
s.t.  and
and  where
where  and
and  .
.
The preservation result allows for a longer signature, to model entering the scope of a  expression or the arms of a match. We implicitly assume that, in the given typing derivation, all types are well-formed under the local signature: for any subderivation of
expression or the arms of a match. We implicitly assume that, in the given typing derivation, all types are well-formed under the local signature: for any subderivation of  , it is the case that
, it is the case that  .
.
Theorem 6
(Preservation). If  and
and  and
and  then there exists
then there exists  such that
such that  where
where  .
.
Theorem 7
(Progress). If  and
and  then
then  is a value or there exists
is a value or there exists  such that
such that  .
.
7 Bidirectional Typing
The type assignment system in Fig. 6 is not syntax-directed, because the rules  and
and  apply to any shape of expression. Nor is the system directed by the syntax of types: rule
apply to any shape of expression. Nor is the system directed by the syntax of types: rule  can conclude
can conclude  for any type
for any type  that is a supertype of some other type
that is a supertype of some other type  . Finally, while the choice to apply rule
. Finally, while the choice to apply rule  is guided by the shape of the expression—it must be a constructor application
is guided by the shape of the expression—it must be a constructor application  —the resulting sort is not uniquely determined, since the signature can have multiple constructor typings for
—the resulting sort is not uniquely determined, since the signature can have multiple constructor typings for  .
.
Fortunately, obtaining an algorithmic system is straightforward, following previous work with datasort refinements and intersection types. We follow the bidirectional typing recipe of Davies and Pfenning (2000); Davies (2005); Dunfield and Pfenning (2004):
-
1.
Split the typing judgment into checking
 and synthesis
and synthesis  judgments. In the checking judgment, the type
judgments. In the checking judgment, the type 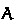 is input (it might be given via type annotation); in the synthesis judgment, the type
is input (it might be given via type annotation); in the synthesis judgment, the type 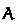 is output.
is output. -
2.
Allow change of direction: Change the subsumption rule to synthesize a type, then check if it is a subtype of a type being checked against; add an annotation rule that checks
 against
against  in the annotated expression
in the annotated expression 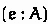 .
. -
3.
In each introduction rule, e.g.
 , make the conclusion a checking judgment; in each elimination rule, e.g.
, make the conclusion a checking judgment; in each elimination rule, e.g.  , make the premise that contains the eliminated connective a synthesis judgment.
, make the premise that contains the eliminated connective a synthesis judgment. -
4.
Make the other judgments in the rules either checking or synthesizing, according to what information is available. For example, the premise of
 becomes a checking judgment, because we know
becomes a checking judgment, because we know 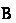 from the conclusion.
from the conclusion. -
5.
Since the subsumption rule cannot synthesize, add rules such as
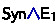 , which were admissible in the type assignment system.
, which were admissible in the type assignment system.
This yields the rules in Fig. 12. (Rules for the match typing judgment  can be obtained from Fig. 10 by replacing “:” in “
can be obtained from Fig. 10 by replacing “:” in “ ” and “
” and “ ” with “
” with “ ”.) While this system is much more algorithmic than Fig. 6, the presence of intersection types requires backtracking: if we apply a function of type
”.) While this system is much more algorithmic than Fig. 6, the presence of intersection types requires backtracking: if we apply a function of type  , we need to synthesize
, we need to synthesize  first; if we subsequently fail (e.g. if the argument has type \(\mathsf {odd}\)), we backtrack and try
first; if we subsequently fail (e.g. if the argument has type \(\mathsf {odd}\)), we backtrack and try  . Similarly, if the signature contains several typings for a constructor
. Similarly, if the signature contains several typings for a constructor  , we may need to try rule
, we may need to try rule  with each typing.
with each typing.
Type-checking for this system is almost certainly PSPACE-complete (Reynolds 1996); however, the experience of Davies (2005) shows that a similar system, differing primarily in whether the signature can be extended, is practical if certain techniques, chiefly memoization, are used.
Using these rules, annotations are required exactly on (1) the entire program  (if
(if  is a checked form, such as a
is a checked form, such as a  ) and (2) expressions not in normal form, such as a
) and (2) expressions not in normal form, such as a  immediately applied to an argument, a recursive function declaration, or a let-binding (assuming the rule for let synthesizes a type for the bound expression). Rules with “more synthesis”—such as a synthesizing version of
immediately applied to an argument, a recursive function declaration, or a let-binding (assuming the rule for let synthesizes a type for the bound expression). Rules with “more synthesis”—such as a synthesizing version of  —could be added along the lines of previous bidirectional type systems (Xi 1998; Dunfield and Krishnaswami 2013).
—could be added along the lines of previous bidirectional type systems (Xi 1998; Dunfield and Krishnaswami 2013).
Following Davies
(2005), an annotation can list several types  . Rule
. Rule  chooses one of these, backtracking if necessary. Multiple types may be needed if a
chooses one of these, backtracking if necessary. Multiple types may be needed if a  -term is checked against intersection type: when checking
-term is checked against intersection type: when checking  against
against  , the type of
, the type of  will be
will be  inside the left subderivation of
inside the left subderivation of  , but \(\mathsf {odd}\) inside the right subderivation. Thus, if we annotate
, but \(\mathsf {odd}\) inside the right subderivation. Thus, if we annotate  with
with  , the check against
, the check against  fails; if we annotate
fails; if we annotate  with \(\mathsf {odd}\), the check against
with \(\mathsf {odd}\), the check against  fails. For a less contrived example, and for a variant annotation form that reduces backtracking, see Dunfield and Pfenning
(2004).
fails. For a less contrived example, and for a variant annotation form that reduces backtracking, see Dunfield and Pfenning
(2004).
In the appendix, we prove that our bidirectional system is sound and complete with respect to our type assignment system:
Theorem 8
(Bidirectional soundness). If  or
or  then
then  where
where  is
is  with all annotations erased.
with all annotations erased.
Theorem 9
(Annotatability). If  then:
then:
-
(1)
There exists
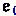 such that
such that  and
and  .
. -
(2)
There exists
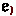 such that
such that  and
and  .
.
We also prove that the  and
and  judgments are decidable (Appendix, Theorem 10).
judgments are decidable (Appendix, Theorem 10).
8 Related Work
Datasort Refinements. Freeman and Pfenning
(1991) introduced datasort refinements with intersection types, defined the refinement restriction (where  is well-formed only if
is well-formed only if  and
and  are refinements of the same type), and developed an inference algorithm in the spirit of abstract interpretation. As discussed earlier, the lack of annotations not only makes the types difficult to see, but makes inference prone to finding long, complex types that include accidental invariants.
are refinements of the same type), and developed an inference algorithm in the spirit of abstract interpretation. As discussed earlier, the lack of annotations not only makes the types difficult to see, but makes inference prone to finding long, complex types that include accidental invariants.
Davies (2005), building on the type system developed by Davies and Pfenning (2000), used a bidirectional typing algorithm, guided by annotations on redexes. This system supports parametric polymorphism through a front end based on Damas–Milner inference, but—like Freeman’s system—does not support extensible refinements. Davies’s CIDRE implementation (Davies 2013) goes beyond his formalism by allowing a single type to be refined via multiple declarations, but this has no formal basis; CIDRE appears to simply gather the multiple declarations together, and check the entire program using the combined declaration, even when this violates the expected scoping rules of SML declarations.
Datasort refinements were combined with union types and indexed types by Dunfield and Pfenning (2003, 2004), who noticed the expressive power of nominal subsorting, called “invaluable refinement” (Dunfield 2007b, pp. 113, 220–230).
Giving multiple refinement declarations for a single datatype was mentioned early on, as future work: “embedded refinement type declarations” (Freeman and Pfenning 1991, p. 275); “or even ...declarations that have their scope limited” (Freeman 1994, p. 167); “it does seem desirable to be able to make local datasort declarations” (Davies 2005, p. 245). But the idea seems not to have been pursued.
Logical Frameworks. In the logical framework LF (Harper et al. 1993), data is characterized by declaring constructors with their types. In this respect, our system is closer to LF than to ML: LF doesn’t require all of a type’s constructors to be declared together. By itself, LF has no need for inversion principles. However, systems such as Twelf (Pfenning and Schürmann 1999), Delphin (Poswolsky and Schürmann 2009) and Beluga (Pientka and Dunfield 2010) use LF as an object-level language but also provide meta-level features. One such feature is coverage (exhaustiveness) checking, which needs inversion principles for LF types. Thus, these systems mark a type as frozen when its inversion principle is applied (to process %covers in Twelf, or a case expression in Beluga); they also allow the user to mark types as frozen. These systems lack subtyping and subsorting; once a type is frozen, it is an error to declare a new constructor for it.
Lovas (2010) extended LF with refinements and subsorting, and developed a constraint-based algorithm for signature checking. This work did not consider meta-level features such as coverage checking, so it yields no immediate insights about inversion principles or freezing. Since Lovas’s system takes the subsorting relation directly from declarations, rather than by inferring it from a grammar, it supports what Dunfield (2007b) called invaluable refinements; see Lovas’s example (Lovas 2010, pp. 145–147).
Indexed Types and Refinement Types. As the second generation of datasort refinements (exemplified by the work of Davies and Pfenning) began, so did a related approach to lightweight type-based verification: indexed types or limited dependent types (Xi and Pfenning 1999; Xi 1998), in which datatypes are refined by indices drawn from a (possibly infinite) constraint domain. Integers with linear inequalities are the standard example of an index domain; another good example is physical units or dimensions (Dunfield 2007a). More recent work in this vein, such as liquid types (Rondon et al. 2008), uses “refinement types” for a mechanism close to indexed types.
Datasort refinements have always smelled like a special case of indexed types. At the dawn of indexed types (and the second generation of datasort refinements), the relationship was obscured by datasorts’ “fellow traveller”, intersection types, which were absent from the first indexed type systems, and remain absent from the approaches now called “refinement types”. That is, while datasorts themselves strongly resemble a specific form of indices—albeit related by a partial order (subtyping), rather than by equality—and would thus suggest that indexed type systems subsume datasort refinement type systems, the inclusion of intersection types confounds such a comparison. Intersection types are present, along with both datasorts and indices, in Dunfield and Pfenning (2003) and Dunfield (2007b); the relationship is less obscured. But no one has given an encoding of types with datasorts into types with indices, intersections or no.
The focus of this paper is a particular kind of extensibility of datasort refinements, so it is natural to ask whether indexed types and (latter-day) refinement types have anything similar. Indexed types are not immediately extensible: both Xi’s DML and Dunfield’s Stardust require that a given datatype be refined exactly once. Thus, a particular list type may carry its length, or the value of its largest element, or the parity of its boolean elements. By refining the type with a tuple of indices, it may also carry combinations of these, such as its length and its largest element. Subsequent uses of the type can leave out some of the indices, but the combination must be stated up front.
However, some of the approaches descended from DML, such as liquid types, allow refinement with a predicate that can mention various attributes. These attributes are declared separately from the datatype; adding a new attribute does not invalidate existing code. Abstract refinement types (Vazou et al. 2013) even allow types to quantify over predicates.
Setting aside extensibility, datasort refinements can express certain invariants more clearly and succinctly than indexed types (and their descendants).
Program Analysis. Koot and Hage (2015) formulate a type system that analyzes where exceptions can be raised, including match exceptions raised by nonexhaustive case expressions. This system appears to be less precise than datasorts, but has advantages typical to program analysis: no type annotations are required.
9 Future Work
Modular Refinements. This paper establishes a critical mechanism for extensible refinements, safe signature extension, in the setting of a core language without modules: refinements are lexically scoped. To scale up to a language with modules, we need to ask: what notions of scope are appropriate? For example, a strict  -calculus interpreter could be refined with a sort \(\mathsf {val}\) of values, while a lazy interpreter could be refined with a sort \(\mathsf {whnf}\) of terms in weak head normal form. If every \(\mathsf {val}\) is a \(\mathsf {whnf}\), we might want to have
-calculus interpreter could be refined with a sort \(\mathsf {val}\) of values, while a lazy interpreter could be refined with a sort \(\mathsf {whnf}\) of terms in weak head normal form. If every \(\mathsf {val}\) is a \(\mathsf {whnf}\), we might want to have  . In the present system, these two refinements could be in separate declare blocks; in that case, \(\mathsf {val}\) and \(\mathsf {whnf}\) could not both be in scope, and the subsorting is not well-formed. Alternatively, one declare block could be nested inside the other. In that case,
. In the present system, these two refinements could be in separate declare blocks; in that case, \(\mathsf {val}\) and \(\mathsf {whnf}\) could not both be in scope, and the subsorting is not well-formed. Alternatively, one declare block could be nested inside the other. In that case,  could be given in the nested block, since it would not add new subsortings within the outer refinement. In a system with modules, we would likely want to have
could be given in the nested block, since it would not add new subsortings within the outer refinement. In a system with modules, we would likely want to have  , at least for clients of both modules; such backpatching is currently not allowed, but should be safe since the new subsorting crosses two independent signature blocks (the block declaring \(\mathsf {val}\) and the block declaring \(\mathsf {whnf}\)) without changing the subsortings within each block.
, at least for clients of both modules; such backpatching is currently not allowed, but should be safe since the new subsorting crosses two independent signature blocks (the block declaring \(\mathsf {val}\) and the block declaring \(\mathsf {whnf}\)) without changing the subsortings within each block.
Type Polymorphism. Standard parametric polymorphism is absent in this paper, but it should be feasible to follow the approach of Davies (2005), as long as the unrefined datatype declarations are not themselves extensible (which would break signature well-formedness, even without polymorphism).
Datasort Polymorphism. Extensible signatures open the door to sort-bounded polymorphism. In our current system, a function that iterates over an abstract syntax tree and  -renames free variables—which would conventionally have the type
-renames free variables—which would conventionally have the type  —must be duplicated, even though the resulting tree has the same shape and the same constructors, and therefore should always produce a tree of the same sort as the input tree (at least, if the free variables are not specified with datasorts). We would like the function to check against a polymorphic type
—must be duplicated, even though the resulting tree has the same shape and the same constructors, and therefore should always produce a tree of the same sort as the input tree (at least, if the free variables are not specified with datasorts). We would like the function to check against a polymorphic type  , which works for any sort
, which works for any sort  below
below  .
.
We would like to reason “backwards” from a pattern match over a polymorphic sort variable  . For example, if a value of type
. For example, if a value of type  matches the pattern
matches the pattern  , then we know that
, then we know that  for some sorts
for some sorts  and
and  . The recursive calls on
. The recursive calls on  and
and  must preserve the property of being in
must preserve the property of being in  and
and  , so
, so  has type
has type  , as needed. The mechanisms we have developed may be a good foundation for adding sort-bounded polymorphism: the \(\mathsf {intersect}\) function would need to return a signature, as well as a context and type, so that the constructor typing
, as needed. The mechanisms we have developed may be a good foundation for adding sort-bounded polymorphism: the \(\mathsf {intersect}\) function would need to return a signature, as well as a context and type, so that the constructor typing  can be made available.
can be made available.
Implementation. Currently, we have a prototype of a few pieces of the system, including a parser and implementations of the  judgment and the \(\mathsf {intersect}\) function. Experimenting with these pieces was helpful during the design of the system (and reassured us that the most novel parts of our system can be implemented), but they fall short of a usable implementation.
judgment and the \(\mathsf {intersect}\) function. Experimenting with these pieces was helpful during the design of the system (and reassured us that the most novel parts of our system can be implemented), but they fall short of a usable implementation.
Notes
- 1.
A regular tree grammar is like a regular grammar (the class of grammars equivalent to regular expressions), but over trees instead of strings (Comon et al. 2008); the leftmost terminal symbol in a production of a regular grammar corresponds to the symbol at the root of a tree.
- 2.
Under the traditional formulation where each constructor has just one type in a signature, the relationship between the old signature
 and the new signature would be slightly more complicated: the old signature might contain
and the new signature would be slightly more complicated: the old signature might contain  , and the new signature
, and the new signature  , and we would need to explicitly eliminate the intersection to expose the old type
, and we would need to explicitly eliminate the intersection to expose the old type 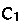 . In our formulation, the new signature appends additional typings for
. In our formulation, the new signature appends additional typings for  while keeping the typing
while keeping the typing  intact.
intact.
References
Comon, H., Dauchet, M., Gilleron, R., Jacquemard, F., Lugiez, D., Tison, S., Tommasi, M.: Tree automata techniques and applications (2008). https://gforge.inria.fr/frs/download.php/file/10994/tata.pdf. Accessed 18 Nov 2008
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Principles of Programming Languages, pp. 238–252 (1977)
Davies, R.: Practical refinement-type checking. Ph.D. thesis, Carnegie Mellon University, CMU-CS-05-110 (2005)
Davies, R.: SML checker for intersection and datasort refinements (pronounced “cider”) (2013). https://github.com/rowandavies/sml-cidre
Davies, R., Pfenning, F.: Intersection types and computational effects. In: ICFP, pp. 198–208 (2000)
Dunfield, J.: Refined typechecking with stardust. In: Programming Languages Meets Program Verification (PLPV 2007) (2007a)
Dunfield, J.: A unified system of type refinements. Ph.D. thesis, Carnegie Mellon University, CMU-CS-07-129 (2007b)
Dunfield, J., Krishnaswami, N.R.: Complete and easy bidirectional typechecking for higher-rank polymorphism. In: ICFP (2013). arXiv:1306.6032
Dunfield, J., Pfenning, F.: Type assignment for intersections and unions in call-by-value languages. In: Gordon, A.D. (ed.) FoSSaCS 2003. LNCS, vol. 2620, pp. 250–266. Springer, Heidelberg (2003). doi:10.1007/3-540-36576-1_16
Dunfield, J., Pfenning, F.: Tridirectional typechecking. In: Principles of Programming Languages, pp. 281–292 (2004)
Freeman, T.: Refinement types for ML. Ph.D. thesis, Carnegie Mellon University, CMU-CS-94-110 (1994)
Freeman, T., Pfenning, F.: Refinement types for ML. In: Programming Language Design and Implementation, pp. 268–277 (1991)
Gentzen, G.: Untersuchungen über das logische Schließen. Mathematische Zeitschrift 39, 176–210, 405–431 (1934). English translation, Investigations into logical deduction. In: Szabo, M. (ed.) Collected Papers of Gerhard Gentzen, pp. 68–131. North-Holland (1969)
Harper, R., Honsell, F., Plotkin, G.: A framework for defining logics. J. ACM 40(1), 143–184 (1993)
Kennedy, A.: Programming languages and dimensions. Ph.D. thesis, University of Cambridge (1996)
Koot, R., Hage, J.: Type-based exception analysis for non-strict higher-order functional languages with imprecise exception semantics. In: Proceedings of the Workshop on Partial Evaluation and Program Manipulation, pp. 127–138 (2015)
Lovas, W.: Refinement types for logical frameworks. Ph.D. thesis, Carnegie Mellon University, CMU-CS-10-138 (2010)
Pfenning, F., Schürmann, C.: System description: Twelf—a meta-logical framework for deductive systems. In: Ganzinger, H. (ed.) CADE 1999. LNCS (LNAI), vol. 1632, pp. 202–206. Springer, Heidelberg (1999). doi:10.1007/3-540-48660-7_14
Pientka, B., Dunfield, J.: Beluga: a framework for programming and reasoning with deductive systems (system description). In: Giesl, J., Hähnle, R. (eds.) IJCAR 2010. LNCS (LNAI), vol. 6173, pp. 15–21. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14203-1_2
Poswolsky, A., Schürmann, C.: System description: Delphin–a functional programming language for deductive systems. In: International Workshop on Logical Frameworks and Meta-Languages: Theory and Practice (LFMTP 2008). Electronic Notes in Theoretical Computer Science, vol. 228, pp. 135–141 (2009)
Reynolds, J.C.: Types, abstraction, and parametric polymorphism. In: Information Processing 83, pp. 513–523. Elsevier (1983). http://www.cs.cmu.edu/afs/cs/user/jcr/ftp/typesabpara.pdf
Reynolds, J.C.: Design of the programming language Forsythe. Technical report CMU-CS-96-146, Carnegie Mellon University (1996)
Rondon, P., Kawaguchi, M., Jhala, R.: Liquid types. In: Programming Language Design and Implementation, pp. 159–169 (2008)
Vazou, N., Rondon, P.M., Jhala, R.: Abstract refinement types. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 209–228. Springer, Heidelberg (2013). doi:10.1007/978-3-642-37036-6_13
Wright, A.K.: Simple imperative polymorphism. Lisp Symbolic Comput. 8(4), 343–355 (1995)
Xi, H.: Dependent types in practical programming. Ph.D. thesis, Carnegie Mellon University (1998)
Xi, H., Pfenning, F.: Dependent types in practical programming. In: Principles of Programming Languages, pp. 214–227 (1999)
Zeilberger, N.: The logical basis of evaluation order and pattern-matching. Ph.D. thesis, Carnegie Mellon University, CMU-CS-09-122 (2009)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Dunfield, J. (2017). Extensible Datasort Refinements. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_18
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_18
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)

















 then
then  .
. then
then  .
. then
then  .
. and synthesis
and synthesis  judgments. In the checking judgment, the type
judgments. In the checking judgment, the type 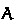 is input (it might be given via type annotation); in the synthesis judgment, the type
is input (it might be given via type annotation); in the synthesis judgment, the type 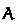 is output.
is output. against
against  in the annotated expression
in the annotated expression 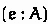 .
. , make the conclusion a checking judgment; in each elimination rule, e.g.
, make the conclusion a checking judgment; in each elimination rule, e.g.  , make the premise that contains the eliminated connective a synthesis judgment.
, make the premise that contains the eliminated connective a synthesis judgment. becomes a checking judgment, because we know
becomes a checking judgment, because we know  from the conclusion.
from the conclusion.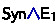 , which were admissible in the type assignment system.
, which were admissible in the type assignment system.
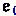 such that
such that  and
and  .
.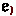 such that
such that  and
and  .
. and the new signature would be slightly more complicated: the old signature might contain
and the new signature would be slightly more complicated: the old signature might contain  , and the new signature
, and the new signature  , and we would need to explicitly eliminate the intersection to expose the old type
, and we would need to explicitly eliminate the intersection to expose the old type 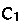 . In our formulation, the new signature appends additional typings for
. In our formulation, the new signature appends additional typings for  while keeping the typing
while keeping the typing  intact.
intact.