Abstract
In this paper, we model the behavior of an epistemic agent that faces a deliberation against a background of oughts, beliefs and information. We do this by introducing a dynamic epistemic logic where ought operators are defined and release of information makes beliefs and oughts co-vary. The static part of the logic extends single-agent Conditional Doxastic Logic by combining dyadic operators for conditional beliefs and oughts that are interpreted over two distinct preorders. The dynamic part of the logic introduces concurrent upgrade operators, which are interpreted on operations that change the two preorders in the same way, thus generating the covariation of beliefs and oughts. The effect of the covariation is that, after receiving new information, the agent will change both her beliefs and her oughts accordingly, and in deliberating, she will pick up the best states among those she takes to be the most plausible.
The author wishes to thank two anonymous reviewers and Ilaria Canavotto, Davide Grossi, Carlo Proietti for their helpful comments. Research for this paper was carried while the author was a Marie Curie IE Fellow with the WADOXA project at the Institute of Logic, Language and Computation, University of Amsterdam (2015–2016).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
Also, we do not presuppose that the deliberating agent has a particular position with respect to the issue in question (for instance, some kind of authority). We attribute deliberation to any agent that can assess what ought to be the case on the ground of believed circumstances.
- 3.
- 4.
A preorder \(\mathcal {R}\) is connected if \(\forall s,s'\in S: \mathcal {R}(s,s')\) or \(\mathcal {R}(s',s)\). It is upward well-founded if, for every \(U\ \subseteq \ S\), if \(U \ne \emptyset \), then
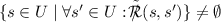 —the set of the ‘most \(R \)’ among the states in U is nonempty. Here,
—the set of the ‘most \(R \)’ among the states in U is nonempty. Here, 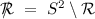 , and \(\tilde{\mathcal {R}}(s,s')\) is short for ‘\(\mathcal {R}(s,s')\) and
, and \(\tilde{\mathcal {R}}(s,s')\) is short for ‘\(\mathcal {R}(s,s')\) and 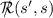 ’.
’. - 5.
We omit the definition for the Boolean constructions, which is standard.
- 6.
That is, their valuations do not vary across states in S of a given model \(\mathcal {M}\).
- 7.
Of course, we could also define \(\mathcal {K}\phi \) as \(\mathcal {O}^{\lnot \phi }\bot \). However, given the conceptual nexus between knowledge and belief, we prefer the definition above.
- 8.
- 9.
Two states s and \(s'\) are equally good if \(R_{\mathcal {O}^{}}(s,s')\) and \(R_{\mathcal {O}^{}}(s',s)\). They are equally plausible if \(R_{\mathcal {B}^{}}(s,s')\) and \(R_{\mathcal {B}^{}}(s',s)\).
- 10.
Unless, of course, there is another formula \(\theta \) such that \(\{\mathcal {B}^{\top }\theta ,\mathcal {O}^{\theta }\psi ,\mathcal {O}^{\top }\psi \}\).
- 11.
Under this reading, the validity of \(\mathcal {O}^{\phi }\phi \) does not cause any concern, even in cases where \(\mathcal {O}^{\top }\lnot \phi \) is satisfied: the best among the scenarios where Jones steals something are still scenarios where he steals something.
- 12.
As for the missing arrows, remember that concurrent upgrade \(\upuparrows p\) leaves relations within the p- and \(\lnot p\)-zones as they were in Fig. 1.
- 13.
These prove especially interesting. In contrast to announcements of factual formulas, announcements of \(\top \),\(\bot \), or any (true or false) modal formula in \(\mathcal {L}_{}\) cannot change the initial model \(\mathcal {M}\). An interesting case holds when Moore sentences are (unsuccessfully) announced. We will not face these cases here, and we refer the reader to [9] for them.
- 14.
As for the missing arrows and curves, remember that concurrent upgrade \(\upuparrows s\) leaves relations within the s- and \(\lnot s\)-zones as they were in Fig. 3. This helps with the missing arrows.
- 15.
Just to get a concrete feeling of this: the fact (or information) that Jones steals does not make stealing (by Jones) norm-abiding.
- 16.
This reading relies on the fact that \(\mathcal {K}\) is a universal modality in our framework, to the effect that the above definition equates with \([\![d]\!]^{\mathcal {M}}\ \subseteq \ [\![\phi ]\!]^{\mathcal {M}}\) in our framework. The definition extends perfect knowledge of the agent to the new deontic component.
- 17.
Any model \(\mathcal {M}\) satisfying \(\mathcal {K}(d\rightarrow p)\) and \([\upuparrows \lnot p]\mathcal {B}^{\top }\lnot p\) fails to satisfy \([\upuparrows \lnot p](\mathcal {B}^{\top }\lnot p\rightarrow \Box \lnot p)\). Indeed, since d and p contains no modal operators, the interpretation of d and p does not change in the upgraded model, to the effect that \([\![d]\!]^{\mathcal {M}^{\upuparrows p}}\ \subseteq \ [\![p]\!]^{\mathcal {M}^{\upuparrows p}}\).
References
Anderson, A.R.: The formal analysis of normative concepts. Am. Sociol. Rev. 22, 9–17 (1967)
Baltag, A., Moss, L.S.: Logics for epistemic programs. Synthese 139, 165–224 (2004)
Baltag, A., Smets, S.: Conditional doxastic models: a qualitative approach to dynamic belief revision. Electron. Notes Theor. Comput. Sci. 165, 5–21 (2006)
Baltag, A., Smets, S.: A Qualitative Theory of Dynamic Interactive Belief Revision. Amsterdam University Press, Amsterdam (2008)
Baltag, A., Smets, S., Zvesper, J.A.: Keep hoping for rationality: a solution to the backward induction paradox. Synthese 169(2), 301–333 (2009)
Blackburn, P., de Rijke, M., Venema, Y.: Modal Logic. Cambridge University Press, Cambridge (2001)
Board, O.: Dynamic interactive epistemology. Games Echonomic Behav. 49(1), 49–80 (2002)
Cariani, F., Kaufmann, M., Kaufmann, S.: Deliberative modality under epistemic uncertainty. Linguist. Philos. 36, 225–259 (2013)
Ditmarsch, H., van der Hoek, W., Kooi, B.: Dynamic Epistemic Logic. Springer, Berlin (2007)
Gerbrandy, J., Groeneveld, J.: Reasoning about information change. J. Logic Lang. Inform. 6(2), 147–169 (1997)
Hansson, B.: An analysis of some deontic logics. Noûs 3, 373–398 (1969)
Hendriks, V.F., Hansen, P.G.: Infostorms, 2nd ed. Copernicus/Springer, New York/Berlin (2015)
Lang, J., van der Torre, L., Weydert, E.: Hidden uncertainty in the logical representation of desires. In: Proceedings of the XVIII IJCAI, pp. 685–690. Morgan Kaufmann Publisher, Inc., San Francisco (CA) (2003)
Liu, F.: Reasoning about Preference Dynamics. Springer, Berlin (2011)
Moore, G.E.: Principia Ethica. Cambridge University Press, Cambridge (1903)
Pacuit, E., Parikh, R., Cogan, E.: The logic of knowledge based obligations. Synthese 149, 311–341 (2006)
Parent, J.: Maximality vs optimality in dyadic deontic logic. J. Philos. Logic 43(6), 1101–1128 (2014)
Proietti, C., Olsson, E.: A DDL approach to pluralistic ignorance and collective belief. J. Philos. Logic 43, 499–515 (2014)
Spohn, W.: An analysis of Hansson’s dyadic deontic logics. J. Philos. Logic 4, 237–252 (1975)
van Benthem, J.: Dynamic logic of belief revision. J. Appl. Non-Classical Logic 17(2), 129–155 (2007)
van Benthem, J., Grossi, D., Liu, F.: Priority structures in deontic logic. Theoria 83, 116–152 (2014)
van Benthem, J., Liu, F.: Dynamic logic of preference upgrade. J. Appl. Non-Classical Logic 17(2), 157–182 (2007)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Ciuni, R. (2017). Conditional Doxastic Logic with Oughts and Concurrent Upgrades. In: Baltag, A., Seligman, J., Yamada, T. (eds) Logic, Rationality, and Interaction. LORI 2017. Lecture Notes in Computer Science(), vol 10455. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-55665-8_21
Download citation
DOI: https://doi.org/10.1007/978-3-662-55665-8_21
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-55664-1
Online ISBN: 978-3-662-55665-8
eBook Packages: Computer ScienceComputer Science (R0)


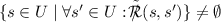 —the set of the ‘most
—the set of the ‘most 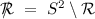 , and
, and 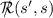 ’.
’.