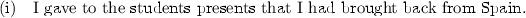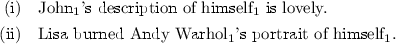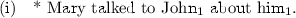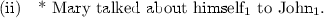Abstract
In this paper we present a treatment for anaphoric pronouns and reflexives in a Type Logical Grammar. To this end, we introduce structural modalities into the left pronominal rule of the categorial calculus with limited contraction LLC [8]. Following a proposal due to Hepple [6], we also sketch an analysis for the long-distance anaphora seg from Icelandic.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Although these languages contain this kind of simple (also weak) reflexive form, their syntactic behavior is not the same in all of them (cf. for example, [5]).
- 2.
Hence, we restrict ourselves to what some theories call anaphoric coreference, not binding (cf. [2, 21]). Though it is generally accepted that reflexives and reciprocals behave in the same way with respect to binding conditions, their semantic value diverges. For this reason, we also do not deal with reciprocal anaphors.
- 3.
However, a version of Jaeger’s rules that also allows cases of cataphora is presented in [17].
- 4.
Jaeger is not only concerned with anaphoric pronouns but also with other anaphoric phenomena, such as ellipsis of VP.
- 5.
As usual, we use n for proper names, s for sentences, cn for common nouns and pp for prepositional phrases.
- 6.
- 7.
Everaert [4] uses these sentences to evaluate the scope and limits of several generative models for binding.
- 8.
Strictly speaking, we split the |R rule of LLC for the case where \(n=1\) and X is the empty sequence \(\epsilon \). As we shall show in the Appendix, the proof of principal Cut for the new rules requires using bracketed versions of the structural rules of Permutation and Expansion. In order to avoid a proof of a pronominal type \(C\Vert A\) for any type C, the antecedent type A of the rule \(\Vert \)R has to be left-peripheral.
- 9.
From Sect. 4, the |L rule (for non-reflexive pronouns) will be renamed \(\Vert \)L\(_{a}\), and \(\Vert \)L will have to be read as \(\Vert \)L\(_{p}\). Though we shall retain |L for reflexives only, we will rename it |L\(_{a}\) for the sake of uniformity.
- 10.
As we shall see later, the formula B in the \(\Vert \)L rule will have a bracketed structure [B] in most cases.
- 11.
A Type-Logical sequent calculus generally contains one left and one right rules for each type-constructor. Since in our proposal the reflexive type-constructor uses only a left rule, our approach is non-standard.
- 12.
In order to distinguish subject and object pronouns, we could assign the lifted type \((s\Vert n)/(n\backslash s)\) to the former (cf. [17]). Although at first glance it would seem that a lifted type—\((s/n)\backslash (s\Vert n)\)—is also adequate to categorize an object pronoun like him, it is not clear how we could deal with Exceptional Case Marked (ECM) constructions, in which the semantic argument of the embedded infinitive clause surfaces with accusative case. Indeed, if him were assigned \((s/n)\backslash (s\Vert n)\) because of its surface form, it would combine with a verb phrase to the left, like a real object complement does. But if this were the case, the subject slot of the embedded complement clause would not be saturated and then, the sentential argument of the ECM verb would become unsaturated as well.
- 13.
In passing, we point out that, unlike English, literary Spanish and Italian allow a nominative free or bound pronoun in non-finite complements of propositional verbs [11].
- 14.
Generally, \(\varDelta [\varGamma ]\) indicates a configuration \(\varDelta \) containing a distinguished configuration \(\varGamma \) of types. In our rules, X[Z] would indicate a sequence X with a distinguished structured sequence [Z] of types, and analogously for \(\left\{ Z\right\} \).
- 15.
As an anonymous reviewer pointed out, if the type \((\left\langle n\right\rangle \backslash s)/s\) were assigned to ECM verbs to differentiate them from propositional verbs, it would allow for ungrammatical sentences like (i–ii) below. To block binding of a reflexive in an object position by a non-local antecedent it seems we would have to impose some condition on the sequence \(Z_{1}\) in [|]L\(_{a}\). We plan to address the challenge posed by ECM constructions in future investigations.
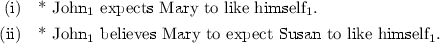
In addition, the side conditions on the [\(\Vert \)]L\(_{a}\) rule inadequately license pronouns to be bound by an antecedent within a conjunctive nominal phrase, as exemplified below. Indeed, Mary is taken as an argument of the functional type commonly assigned to and:
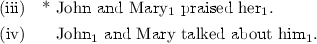
It appears that the unbracketed type assigned to the conjunction and has to be differentiated from the (bracketed) functional types assigned, for example, to of—\((n\backslash n)/\left\langle n \right\rangle \) and ’s—\(\left\langle n\right\rangle \backslash (n/cn)\). A distinction between a collective and a distributive type for and also seems to be relevant: roughly, \(X\backslash X/X\) and \(\left\langle X\right\rangle \backslash X/\left\langle X\right\rangle \), for example. For reasons of space, and since judgments seem to vary among speakers and sentences, we defer this problem to future research.
- 16.
Alternatively, Reinhart and Reuland [22] consider that relies on forms a complex (semantic and syntactic) unit selecting a nominal complement, whilst put selects a prepositional complement. In view of this fact, we would assign the type \((\left\langle n\right\rangle \backslash s)/\left\langle n\right\rangle \) to relies on/upon.
- 17.
Note that the product
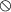 is not a discontinuous (or wrapping) type-constructor, unlike that of [1] or [19]. Since
is not a discontinuous (or wrapping) type-constructor, unlike that of [1] or [19]. Since 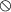 is non-commutative, we would not be able to derive cases of “heavy” NP, as exemplified below. Nevertheless, in the following section we shall adopt a commutative product-type for the treatment of prepositional phrases.
is non-commutative, we would not be able to derive cases of “heavy” NP, as exemplified below. Nevertheless, in the following section we shall adopt a commutative product-type for the treatment of prepositional phrases. 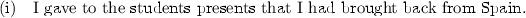
To deal with double-object structures, Hepple [6] extends the L calculus by adding a new slash type-constructor \(\oint \) and a modality \(\triangleright \). Since the slash type-constructor lacks introduction rules, it may encode the hierarchical ordering of the nominal complements; the modality allows the nominal complements to be reordered to obtain the correct surface word-order.
- 18.
We note that a slightly modified version of the rule in Fig. 16 may also be used for anaphors in a complement of possessives, which are not either subject nor object-oriented. Once again, it appears that a distinction between the functional type assigned to of or ’s and and has to be made to prevent He and himself from assigning the type n.
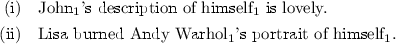
It seems that it could be possible to also encode a hierarchical ordering into the rules for the Lambek slash type-constructors. In this case, it would be possible to deal with subject- and object-oriented anaphors in a uniform way.
- 19.
In some generative theories, the about-phrase is evaluated as an adjunct phrase and thus is separated from the to-phrase or with-phrase complement (cf. [22]). This would explain the ungrammaticality of (40), but not the ungrammaticality of (i) below.
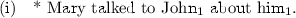
In other theories, the about-phrase, as well as the to-phrase, is considered a verb complement; the difference between these PPs is made by assuming an ordering with respect to their relative obliqueness: the about-phrase is more oblique than the to-phrase (cf. [20]). Since the anaphor has to be bound by a less oblique co-argument, the relationship of relative obliqueness would account for (i) above, but not for (ii) below, where the linear word-order seems to be also relevant.
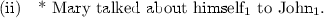
In addition, [3] suggests an approach in which the verb talk (and also speak) and the preposition to are reanalyzed as one verb taking a nominal object (and a prepositional complement) (cf. also [23]). Thus, talk would be analogous to (one of the forms of) tell. To formalize this proposal, besides encoding free linear word-order and relative obliqueness, the syntactic functional type assigned to the talk to-phrase would have to encode discontinuity as well.
- 20.
Since the calculus D also contains a nondeterministic discontinuous product \(\odot \), the type \((n\backslash s)/(pp\odot pp)\) would take the structural ordering into account if the premisses of the right rule were bracketed sequences.
References
Bach, E.: Control in montague grammar. Linguist. Inq. 10(4), 515–531 (1979)
Büring, D.: Pronouns. In: Semantics: An International Handbook of Natural Language Meaning, vol. 2, pp. 971–996 (2011)
Chomsky, N.: Lectures on Government and Binding. Kluwer, Dordrecht (1981)
Everaert, M.: Binding theories: a comparison of grammatical models. In: van Oostendorp, M., Anagnostopoulou, E. (eds.) Progress in Grammar. Articles at the 20th Anniversary of the Comparison of Grammatical Models Group in Tilburg. Meertens Institute, Electronic Publications in Linguistics, Amsterdam (2000)
Hendriks, P., Hoeks, J., Spenader, J.: Reflexive choice in Dutch and German. J. Comp. Ger. Linguist. 17(3), 229–252 (2015)
Hepple, M.: Command and domain constraints in a categorial theory of binding. In: Proceedings of the Eight Amsterdam Colloquium, pp. 253–270 (1992)
Jacobson, P.: Towards a variable-free semantics. Linguist. Philos. 22(2), 117–185 (1999)
Jäeger, G.: Anaphora and Type Logical Grammar. Trends in Logic - Studia Logica Library, vol. 24. Springer, Dordrecht (2005). https://doi.org/10.1007/1-4020-3905-0
Lambek, J.: The mathematics of sentence structure. Am. Math. Mon. 65(3), 154–170 (1958)
Marantz, A.P.: On the Nature of Grammatical Relations. Linguistic Inquiry Monographs Ten. The MIT Press, Cambridge (1984)
Mensching, G.: Infinitive constructions with specified subjects: a syntactic analysis of the romance languages (2000)
Moortgat, M.: Multimodal linguistic inference. J. Logic Lang. Inform. 5(3–4), 349–385 (1996)
Morrill, G.: Intensionality and boundedness. Linguist. Philos. 13(6), 699–726 (1990)
Morrill, G.: Categorial formalisation of relativisation: pied piping, islands, and extraction sites. Technical report, Departament de Llenguatges i Sistemes Informàtics, Universitat Politècnica de Catalunya (1992)
Morrill, G.: Type Logical Grammar. Categorial Logic of Signs. Springer, Dordrecht (1994). https://doi.org/10.1007/978-94-011-1042-6
Morrill, G., Valentín, O.: On anaphora and the binding principles in categorial grammar. In: Dawar, A., de Queiroz, R. (eds.) WoLLIC 2010. LNCS (LNAI), vol. 6188, pp. 176–190. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13824-9_5
Morrill, G., Valentín, O.: Semantically inactive multiplicatives and words as types. In: Asher, N., Soloviev, S. (eds.) LACL 2014. LNCS, vol. 8535, pp. 149–162. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43742-1_2
Morrill, G., Valentín, O.: Computational coverage of TLG: displacement. In: Proceedings of Empirical Advances in Categorial Grammar, pp. 132–161 (2015)
Morrill, G., Valentín, O., Fadda, M.: The displacement calculus. J. Logic Lang. Inform. 20(1), 1–48 (2011)
Pollard, C., Sag, I.A.: Anaphors in English and the scope of binding theory. Linguist. Inq. 23(2), 261–303 (1992)
Reinhart, T.: Coreference and bound anaphora: a restatement of the anaphora questions. Linguist. Philos. 6(1), 47–88 (1983)
Reinhart, T., Reuland, E.: Reflexivity. Linguist. Inq. 24(4), 657–720 (1993)
Szabolcsi, A.: Bound variables in syntax (are there any?). In: Bartsch, R., van Benthem, J., van Emde Boas, P. (eds.) Semantics and Contextual Expressions, pp. 295–318. Foris, Dordrecht (1989)
Acknowledgment
The author was supported by a doctoral scholarship granted by FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo, process number 2013/08115-1).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
The proof for the Cut elimination theorem requires the use of the following bracketed versions of the structural rules of Permutation and Expansion (Fig. 22). In order to prove Cut Elimination for LLBE we have to consider two more cases for principal Cut: the left premise of Cut is the conclusion of \(\Vert \)L\(_{a}\) or that of \(\Vert \)L\(_{p}\) and the right premise is the conclusion of \(\Vert \)R. These two configurations are given schematically in Figs. 23 and 24. In both cases, the principal Cut is replaced by a Cut of lower degree. Since no rule introduces a formula  into the right side of a sequent (i.e. there are only antecedent occurrences of the formula
into the right side of a sequent (i.e. there are only antecedent occurrences of the formula  ), the Cut formula could not have been derived by applying either of the bracketed structural rules.
), the Cut formula could not have been derived by applying either of the bracketed structural rules.
Rights and permissions
Copyright information
© 2018 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Corbalán, M.I. (2018). Binding Domains: Anaphoric and Pronominal Pronouns in Categorial Grammar. In: Foret, A., Muskens, R., Pogodalla, S. (eds) Formal Grammar . FG 2017. Lecture Notes in Computer Science(), vol 10686. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-56343-4_1
Download citation
DOI: https://doi.org/10.1007/978-3-662-56343-4_1
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-56342-7
Online ISBN: 978-3-662-56343-4
eBook Packages: Computer ScienceComputer Science (R0)





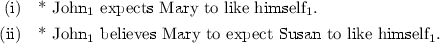
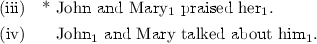
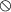 is not a discontinuous (or wrapping) type-constructor, unlike that of [
is not a discontinuous (or wrapping) type-constructor, unlike that of [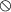 is non-commutative, we would not be able to derive cases of “heavy” NP, as exemplified below. Nevertheless, in the following section we shall adopt a commutative product-type for the treatment of prepositional phrases.
is non-commutative, we would not be able to derive cases of “heavy” NP, as exemplified below. Nevertheless, in the following section we shall adopt a commutative product-type for the treatment of prepositional phrases.