Abstract
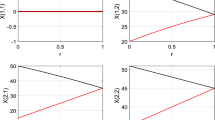
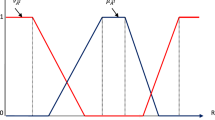
Present paper deals with a multi-objective transportation problem. This problem has equality type constraints and some non-commensurable and conflicting objectives. The above objectives are fuzzy in nature. The problem has been solved by three methods using fuzzy programming approach. A numerical example is also given to compare the results obtained by different methods.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bellman, R.E., Zadeh, L.A.: Decision-making in a Fuzzy Environment. Management Science 17(4), 141–164 (1970)
Bit, A.K., Biswal, M.P., Alam, S.S.: Fuzzy Programming Problem. Fuzzy Sets and Systems 50, 135–141 (1992)
Chen, L.-H., Tsai, F.-C.: Fuzzy Goal Programming with Different Importance and Priorities. European Journal of Operational Research 133, 548–556 (2001)
Diaz, J.A.: Solving Multi-objective Transportation Problem. Ekonom. Mat. Obzor 14, 267–274 (1978)
Diaz, L.A.: Finding a Complete Description of all Efficient Solutions to a Multi-objective Transportation Problem. Ekonom. Mat. Obzor 15, 62–73 (1979)
Dutta, D., Murthy, A.S.: Fuzzy Transportation Problem with Additional Restrictions. ARPN Journal of Engineering and Applied Sciences 5(2), 36–40 (2010)
Hitcbcock, F.L.: The Distribution of a Product from Several Sources to Numerous Localities. J. Math. Phys. 20, 224–230 (1941)
Mahapatra, D.R., Roy, S.K., Biswal, M.P.: Multi-objective Stochastic Transportation Problem involving Log-normal. Journal of Physical Sciences 14, 63–76 (2010)
Ringuest, J.L., Rinks, D.B.: Interaction Solutions for the Linear Multi-objective Transportation Problem. European J. Oper. Res. 32, 96–106 (1987)
Ritha, W., Vinotha, J.M.: Multi-objective Two Stage Fuzzy Transportation Problem. Journal of Physical Sciences 13, 107–120 (2009)
Roy, T.K., Maiti, M.: Multi-objective Inventory Models of Deteriorating with Some Constraints in a Fuzzy Environment. Computers Ops. Res. 25(12), 1085–1095 (1998)
Taha, H.A.: Operation Research, An Introduction, 5th edn. Macmillan, New York (1992)
Tiwari, R.N., Dharmar, S., Rao, J.R.: Fuzzy Goal Programming-an Additive Model. Fuzzy Sets and Systems 24, 27–34 (1987)
Rakesh, V., Biswal, M.P., Biswas, A.: Fuzzy Programming Technique to Solve Mult-objective Transportation Problems with Some Non-linear Membership Functions. Fuzzy Sets and Systems 91, 37–43 (1997)
Yaghoobi, M.A., Tamiz, M.: A Method for Solving Fuzzy Goal Programming Problems Based on Minmax Approach. European Journal of Operational Research 177, 1580–1590 (2007)
Zimmermann, H.-J.: Fuzzy Programming and Linear Programming with Several Objective Functions. Fuzzy Sets and Systems 1, 45–55 (1978)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer India Pvt. Ltd.
About this paper
Cite this paper
Kumar, S., Pandey, D. (2012). Fuzzy Programming Approach to Solve Multi-objective Transportation Problem. In: Deep, K., Nagar, A., Pant, M., Bansal, J. (eds) Proceedings of the International Conference on Soft Computing for Problem Solving (SocProS 2011) December 20-22, 2011. Advances in Intelligent and Soft Computing, vol 130. Springer, India. https://doi.org/10.1007/978-81-322-0487-9_51
Download citation
DOI: https://doi.org/10.1007/978-81-322-0487-9_51
Published:
Publisher Name: Springer, India
Print ISBN: 978-81-322-0486-2
Online ISBN: 978-81-322-0487-9
eBook Packages: EngineeringEngineering (R0)