Abstract
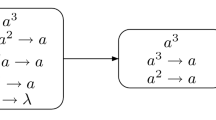
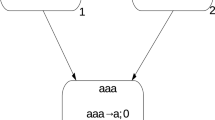
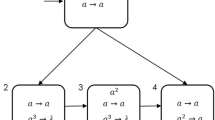
This paper is an attempt to relax the condition of using the rules in a maximally parallel manner in the framework of spiking neural P systems with exhaustive use of rules. To this aim, we consider the minimal parallelism of using rules: if one rule associated with a neuron can be used, then the rule must be used at least once (but we do not care how many times). In this framework, we study the computational power of our systems as number generating devices. Weak as it might look, this minimal parallelism still leads to universality, even when we eliminate the delay between firing and spiking and the forgetting rules at the same time.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Hagan, M.T., Demuth, H.B., Beale, M.H.: Neural Network Design. PWS Publishing, Boston (1996)
Ghosh-Dastidar, S., Adeli, H.: Spiking neural networks. Int. J. Neur. Syst. 19, 295–308 (2009)
Ionescu, M., Păun, G., Yokomori, T.: Spiking neural P systems. Fund. Inform. 71, 279–308 (2006)
Cavaliere, M., Ibarra, O.H., Păun, G., Egecioglu, O., Ionescu, M., Woodworth, S.: Asynchronous spiking neural P systems. Theor. Comput. Sci. 410, 2352–2364 (2009)
Pan, L., Păun, G.: Spiking neural P systems with anti-spikes. Int. J. Comput. Commun. 4, 273–282 (2009)
Ionescu, M., Păun, G., Pérez-Jiménez, M.J., Yokomori, T.: Spiking neural dP systems. Fund. Inform. 111, 423–436 (2011)
Pan, L., Wang, J., Hoogeboom, H.J.: Spiking neural P systems with astrocytes. Neural Comput. 24, 805–825 (2012)
Pan, L., Zeng, X., Zhang, X., Jiang, Y.: Spiking neural P systems with weighted synapses. Neural Process. Lett. 35, 13–27 (2012)
Song, T., Pan, L., Păun, G.: Spiking neural P systems with rules on synapses. Theor. Comput. Sci. 529, 82–95 (2014)
Wang, J., Hoogeboom, H.J., Pan, L., Păun, G., Pérez-Jiménez, M.J.: Spiking neural P systems with weights. Neural Comput. 22, 2615–2646 (2014)
Song, T., Liu, X., Zeng, X.: Asynchronous spiking neural P systems with anti-spikes. Neural Process. Lett. 42, 633–647 (2015)
Song, T., Pan, L.: Spiking neural P systems with rules on synapses working in maximum spiking strategy. IEEE Trans. Nanobiosci. 14, 465–477 (2015)
Song, T., Pan, L.: Spiking neural P systems with rules on synapses working in maximum spikes consumption strategy. IEEE Trans. Nanobiosci. 14, 38–44 (2015)
Song, T., Gong, F., Liu, X., Zhao, Y., Zhang, X.: Spiking neural P systems with white hole neurons. IEEE Trans. Nanobiosci. 15, 666–673 (2016)
Zhao, Y., Liu, X., Wang, W., Adamatzky, A.: Spiking neural P systems with neuron division and dissolution. PLoS ONE 11, e0162882 (2016)
Wu, T., Zhang, Z., Păun, G., Pan, L.: Cell-like spiking neural P systems. Theor. Comput. Sci. 623, 180–189 (2016)
Jiang, K., Chen, W., Zhang, Y., Pan, L.: Spiking neural P systems with homogeneous neurons and synapses. Neurocomputing 171, 1548–1555 (2016)
Song, T., Pan, L.: Spiking neural P systems with request rules. Neurocomputing 193, 193–200 (2016)
Ibarra, O.H., Păun, A., Rodríguez-Patón, A.: Sequential SNP systems based on min/max spike number. Theor. Comput. Sci. 410, 2982–2991 (2009)
Neary, T.: A boundary between universality and non-universality in extended spiking neural P systems. In: Dediu, A.-H., Fernau, H., Martín-Vide, C. (eds.) LATA 2010. LNCS, vol. 6031, pp. 475–487. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13089-2_40
Song, T., Pan, L., Jiang, K., Song, B., Chen, W.: Normal forms for some classes of sequential spiking neural P systems. IEEE Trans. Nanobiosci. 12, 255–264 (2013)
Zhang, X., Zeng, X., Luo, B., Pan, L.: On some classes of sequential spiking neural P systems. Neural Comput. 26, 974–997 (2014)
Wang, X., Song, T., Gong, F., Zheng, P.: On the computational power of spiking neural P systems with self-organization. Sci. Rep. 6, 27624 (2016)
Chen, H., Freund, R., Ionescu, M.: On string languages generated by spiking neural P systems. Fund. Inform. 75, 141–162 (2007)
Krithivasan, K., Metta, V.P., Garg, D.: On string languages generated by spiking neural P systems with anti-spikes. Int. J. Found. Comput. Sci. 22, 15–27 (2011)
Zeng, X., Xu, L., Liu, X.: On string languages generated by spiking neural P systems with weights. Inform. Sci. 278, 423–433 (2014)
Song, T., Xu, J., Pan, L.: On the universality and non-universality of spiking neural P systems with rules on synapses. IEEE Trans. Nanobiosci. 14, 960–966 (2015)
Wu, T., Zhang, Z., Pan, L.: On languages generated by cell-like spiking neural P systems. IEEE Trans. Nanobiosci. 15, 455–467 (2016)
Păun, G., Păun, A.: Small universal spiking neural P systems. Biosystems 90, 48–60 (2007)
Zhang, X., Zeng, X., Pan, L.: Smaller universal spiking neural P systems. Fund. Inform. 87, 117–136 (2008)
Pan, L., Zeng, X.: A note on small universal spiking neural P systems. In: Păun, G., Pérez-Jiménez, M.J., Riscos-Núñez, A., Rozenberg, G., Salomaa, A. (eds.) WMC 2009. LNCS, vol. 5957, pp. 436–447. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11467-0_29
Song, T., Jiang, Y., Shi, X., Zeng, X.: Small universal spiking neural P systems with anti-spikes. J. Comput. Theor. Nanosci. 10, 999–1006 (2013)
Zeng, X., Pan, L., Pérez-Jiménez, M.J.: Small universal simple spiking neural P systems with weights. Sci. China. Inform. Sci. 57, 1–11 (2014)
Metta, V.P., Raghuraman, S., Krithivasan, K.: Small universal spiking neural P systems with cooperating rules as function computing devices. In: Gheorghe, M., Rozenberg, G., Salomaa, A., Sosík, P., Zandron, C. (eds.) CMC 2014. LNCS, vol. 8961, pp. 300–313. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-14370-5_19
Song, T., Pan, L.: A small universal spiking neural P systems with cooperating rules. Rom. J. Inf. Sci. Technol. 17, 177–189 (2014)
Ishdorj, T.-O., Leporati, A., Pan, L., Zeng, X., Zhang, X.: Deterministic solutions to QSAT and Q3SAT by spiking neural P systems with pre-computed resources. Theor. Comput. Sci. 411, 2345–2358 (2010)
Pan, L., Păun, G., Pérez-Jiménez, M.J.: Spiking neural P systems with neuron division and budding. Sci. China Inform. Sci. 54, 1596–1607 (2011)
Song, T., Zheng, P., Wong, M.L., Wang, X.: Design of logic gates using spiking neural P systems with homogeneous neurons and astrocytes-like control. Inform. Sci. 372, 380–391 (2016)
Díaz-Pernil, D., Gutiérrez-Naranjo, M.J.: Semantics of deductive databases with spiking neural P systems. Neurocomputing (2017). https://doi.org/10.1016/j.neucom.2017.07.007
Zeng, X., Song, T., Zhang, X., Pan, L.: Performing four basic arithmetic operations with spiking neural P systems. IEEE Trans. Nanobiosci. 11, 366–374 (2012)
Liu, X., Li, Z., Liu, J., Liu, L., Zeng, X.: Implementation of arithmetic operations with time-free spiking neural P systems. IEEE Trans. Nanobiosci. 14, 617–624 (2015)
Wang, J., Shi, P., Peng, H., Pérez-Jiménez, M.J., Wang, T.: Weighted fuzzy spiking neural P systems. IEEE Trans. Fuzzy Syst. 21, 209–220 (2013)
Peng, H., Wang, J., Pérez-Jiménez, M.J., Wang, H., Shao, J., Wang, T.: Fuzzy reasoning spiking neural P systems for fault diagnosis. Inform. Sci. 235, 106–116 (2013)
Wang, J., Peng, H.: Adaptive fuzzy spiking neural P systems for fuzzy inference and learning. Int. J. Comput. Math. 90, 857–868 (2013)
Wang, T., Zhang, G., Zhao, J., He, Z., Wang, J., Pérez-Jiménez, M.J.: Fault diagnosis of electric power systems based on fuzzy reasoning spiking neural P systems. IEEE Trans. Power Syst. 30, 1182–1194 (2015)
Zhang, G., Rong, H., Neri, F., Pérez-Jiménez, M.J.: An optimization spiking neural P system for approximately solving combinatorial optimization problems. Int. J. Neur. Syst. 24, 1440006 (2014)
Ionescu, M., Păun, G., Yokomori, T.: Spiking neural P systems with exhaustive use of rules. Int. J. Unconv. Comput. 3, 135–154 (2007)
Ciobanu, G., Pan, L., Păun, G., Pérez-Jiménez, M.J.: P systems with minimal parallelism. Theor. Comput. Sci. 378, 117–130 (2007)
Rozenberg, G., Salomaa, A. (eds.): Handbook of Formal Language: Volume 3 Beyond Words. Springer, Heidelberg (1997). https://doi.org/10.1007/978-3-642-59126-6
Păun, G., Rozenberg, G., Salomaa, A. (eds.): The Oxford Handbook of Membrane Computing. Oxford University Press, New York (2010)
Minsky, M.: Computation - Finite and Infinite Machines. Prentice Hall, Englewood Cliffs (1967)
Acknowledgments
This work was supported by National Natural Science Foundation of China (61502063).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Jiang, Y., Luo, F., Luo, Y. (2017). Spiking Neural P Systems with Minimal Parallelism. In: He, C., Mo, H., Pan, L., Zhao, Y. (eds) Bio-inspired Computing: Theories and Applications. BIC-TA 2017. Communications in Computer and Information Science, vol 791. Springer, Singapore. https://doi.org/10.1007/978-981-10-7179-9_10
Download citation
DOI: https://doi.org/10.1007/978-981-10-7179-9_10
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-7178-2
Online ISBN: 978-981-10-7179-9
eBook Packages: Computer ScienceComputer Science (R0)