Keywords

1 Introduction

In recent years, there has been rapid growth of multi-view data and much efforts have witnessed the great significance of learning from multi-view data in many real-world applications. Often, multi-view data, presented in diverse forms or derived from different domains, show heterogeneous characteristics, which is a big challenge for practical tasks such as cross-modal retrieval, machine translation, biometric verification, matching, transfer learning, etc. To address this challenge, two common strategies are mainly adopted. One is to learn distance metrics, the other is to learn a common space. In this paper we focus on the latter, that is, multi-view subspace learning.

Intrinsically, multiple views represent the same underlying semantic data object, therefore, they are inherently correlated to each other. Based on this fact, statical techniques such as canonical correlation analysis (CCA) [11], Kullback-Leibler (KL) divergence [1], mutual information [12] and Hilbert-Schmidt Independence Criterion (HSIC) [6] and so on, to measure correlation (dependence) of two random variables, have been investigated and used for multi-view learning. Especially, CCA is the most popular one among the aforementioned measures.

From the point of multi-view learning, CCA can be regarded as finding the projection matrix for each view of the data object, by which the data can be projected into a common subspace where the low dimensional embeddings are maximally correlated. Due to the encouraging success of CCA, CCA-based approaches have attracted much attention during the past decades. Substantial variants of CCA have been developed for multi-view subspace representations, including unsupervised ones [16, 18, 20], supervised ones [15, 19], sparsity-based ones [4, 10], DNN-based ones [2, 13, 22], etc. Like CCA, considerable attention has been gradually paid to the use of HSIC for the dependence-based tasks of multi-view classification [7], clustering [3], dictionary learning [8, 9]. Concerning these methods, they are supervised ones, which conformably expect the dependence between multi-view data and the corresponding labels to be maximized. However, labels are unknown beforehand in most cases of multi-view learning tasks.

In this paper, we propose an unsupervised dependence maximization model for multi-view subspace learning, referred to as UDM. The proposed UDM is designed specifically for the case of two views, which can be extended to multiple views. Unlike the supervised HSIC-based approaches, UDM aims at maximizing the dependence between two views under the unsupervised setting. Simultaneously, it incorporates the imposed \(\ell _{2,1}\)-norm constraint on the projection matrix for each view as regulations, playing the role of feature selection, which enables more discriminative representations. To solve the optimization problem formulated by UDM, an efficient iterative optimizing algorithm is designed. Experimental results on two real-world cross-modal datasets demonstrate the effectiveness and efficiency of UDM, and show the superiority of UDM over the compared approaches. Convergence curves of the objective function demonstrate the rapid convergence speed of the optimization algorithm.

2 Notations and HSIC

2.1 Notations

To begin with, we introduce some notations used in this paper. For any matrix \(\mathbf{{A}} \in \mathbb {R}^{n\times m}\), \(\mathbf{{A}}^{\cdot \cdot i}\) and \(\mathbf{{A}}^{:j}\) are used to represent its i-th row and j-th column, respectively. \({\left\| \mathbf {A}\right\| }_{2,1}\) is the \(\ell _{2,1}\)-norm of \(\mathbf{{A}}\), defined as \({\left\| \mathbf {A}\right\| }_{2,1}=\sum \limits _{i=1}^n {{{\left\| {{\mathbf{{A}}^{\cdot \cdot i}}} \right\| }_2}}\). \({\left\| \mathbf{{A}} \right\| _{HS}}\) is the Hilbert-Schmidt norm of \(\mathbf {A}\), defined as \({\left\| \mathbf{{A}} \right\| _{HS}} = \sqrt{\sum \limits _{i,j} {a_{ij}^2} } \). Besides, \(tr\left( \cdot \right) \) represents the trace operator, \( \otimes \) the tensor product and \(\mathbf {I}\) an identity matrix with an appropriate size. Throughout the paper, matrices and vectors are represented in bold uppercase and lowercase letters respectively. Variables are represented by conventional letters.

2.2 Hilbert-Schmidt Independence Criteria

Let \({C}_{xy}\) be the cross-covariance function between x and y, \(\varphi (x)\) and \(\phi (y)\) two mapping functions with \(\varphi (x):x \in \mathcal {X} \rightarrow \mathbb {R}\) and \(\phi (y):y \in \mathcal {Y} \rightarrow \mathbb {R}\), \(\mathcal {G}\) and \(\mathcal {H}\) two Reproducing Kernel Hilbert Spaces (RKHSs) in \(\mathcal {X}\) and \(\mathcal {Y}\). The associated positive definite kernels \(k_x\) and \(k_y\) is defined as \(k_x(x,x^T)=<\varPhi (x),\varPhi (x)>_\mathcal{{G}}\) and \(k_y(y,y^T)=<\varPhi (y),\varPhi (y)>_\mathcal{{H}}\). Then cross-covariance \(C_{xy}\) is defined as:

$$\begin{aligned} {C_{xy}} = {E_{xy}}\left[ {\left( {\varphi \left( x \right) - {u_x}} \right) \otimes \left( {\phi \left( y \right) - {u_y}} \right) } \right] . \end{aligned}$$
(1)

where \(u_x\) and \(u_y\) is the expectation of \(\varphi (x)\) and \(\phi (y)\) respectively, i.e. \({u_x} = E\left( {\varphi \left( x \right) } \right) \) and \({u_y} = E\left( {\phi \left( y \right) } \right) \).

Given two independent RKHSs \(\mathcal {G}\), \(\mathcal {H}\) and the joint distribution \(p_{xy}\), HSIC is the Hilbert-Schmidt norm of \(C_{xy}\), defined as:

$$\begin{aligned} HSIC\left( {{p_{xy}},\mathcal {G},\mathcal {H}} \right) : = \left\| {{C_{xy}}} \right\| _{HS}^2. \end{aligned}$$
(2)

In practical applications, the empirical estimate of HSIC is commonly used. Given n finite number of data samples \(Z:=\{(x_1,y_1),\cdots ,(x_N,y_N)\}\), the empirical expression of HSIC is formulated as:

$$\begin{aligned} HSIC\left( {Z,F,G} \right) = {\left( {n - 1} \right) ^{ - 2}}tr\left( {{\mathbf{{K}}_1}{} \mathbf{{H}}{\mathbf{{K}}_2}{} \mathbf{{H}}} \right) . \end{aligned}$$
(3)

where \(\mathbf {\mathbf {K}}_1\) and \(\mathbf {\mathbf {K}}_2\) are two Gram matrices with \(k_{1,ij}=k_1(x_i,x_j)\) and \(k_{2,ij}=k_2(y_i,y_j)\) \((i,j=1,\cdots ,N)\). \(\mathbf {H}=\mathbf {I}-\frac{1}{n}\mathbf {1}_n\mathbf {1}_n^T\), is a centering matrix, and \(\mathbf {1}_n\in \mathbb {R}^n\) is a full-one column vector.

More details about HSIC can be found in literatures [6].

3 Multi-view Subspace Learning Model via Kernel Dependence Maximization

3.1 The Proposed Subspace Learning Model

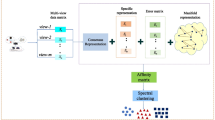
Multi-view subspace learning approaches aim to project different high-dimensional heterogeneous views into a coherent low-dimensional common subspace in linear or nonlinear ways, where samples with the same or similar semantics have the coherent representation, as illustrated in Fig. 1.

Fig. 1.
figure 1

Sketch map of subspace learning for multi-view data

Full size image

In the following, the case of two views is mainly considered. Suppose that there are n pairs of observation samples \(\left\{ {\mathbf{{x}}_1^i,\mathbf{{x}}_2^i} \right\} \in \mathbb {R}^{1\times {d_1}} \times \mathbb {R}^{1\times {d_2}} \), where \(\left\{ {\mathbf{{x}}_1^i} \right\} _{i = 1}^n\) and \(\left\{ {\mathbf{{x}}_2^i} \right\} _{i = 1}^n\) are from view \({\mathbf{{X}}_1} = {\left[ {\mathbf{{x}}_1^1, \cdots ,\mathbf{{x}}_1^n} \right] ^T}\in \mathbb {R}^{n\times {d_1}}\) and view \({\mathbf{{X}}_2} = {\left[ {\mathbf{{x}}_2^1, \cdots ,\mathbf{{x}}_2^n} \right] ^T}\in \mathbb {R}^{n\times {d_2}}\) respectively. \(\left\{ {\mathbf{{x}}_1^i,\mathbf{{x}}_2^i} \right\} \) denotes the i-th pair samples in the sample set \(\left\{ {\mathbf{{x}}_1^i,\mathbf{{x}}_2^i} \right\} _{i = 1}^n\). The goal of this paper is to learn the projection matrix \(\mathbf{{P}}_v(v=1,2)\) for views \(\mathbf{{X}}_v(v=1,2)\) simultaneously. Through \(\mathbf{{P}}_v\), heterogeneous views \(\mathbf{{X}}_v\) are projected into a common subspace \(\mathbf {S}\), where samples \(\mathbf{{x}}_1^i\) and \(\mathbf{{x}}_2^j(i,j=1,\cdots ,n)\) with the same and similar semantics have the coherent representation. Correspondingly, the new representation for \(\mathbf{{X}}_1\) and \(\mathbf{{X}}_2\) in the shared subspace is \(\mathbf{{X}}_1^S = {\mathbf{{X}}_1}{\mathbf{{P}}_1}\) and \(\mathbf{{X}}_2^S = {\mathbf{{X}}_2}{\mathbf{{P}}_2}\). Adopting linear kernel as the kernel measure, kernel matrices \({\mathbf{{K}}_{{\mathrm{{X}}_1}}}\) and \({\mathbf{{K}}_{{\mathrm{{X}}_2}}}\) can be denoted as \({\mathbf{{K}}_{{\mathrm{{X}}_1}}} = \left\langle {\mathbf{{X}}_1^S,\mathbf{{X}}_1^S} \right\rangle = {\mathbf{{X}}_1}{\mathbf{{P}}_1}{} \mathbf{{P}}_1^T\mathbf{{X}}_1^T\) and \({\mathbf{{K}}_{{\mathrm{{X}}_2}}} = \left\langle {\mathbf{{X}}_2^S,\mathbf{{X}}_2^S} \right\rangle = {\mathbf{{X}}_2}{\mathbf{{P}}_2}{} \mathbf{{P}}_2^T\mathbf{{X}}_2^T\). Since multi-view data describe the same semantic object from different levels, they are inherently correlated to each other. Based on HSIC, the proposed unsupervised subspace learning model is formulated as:

$$\begin{aligned} {\begin{matrix} &{}\mathop {\max }\limits _{{\mathbf{{P}}_1},{\mathbf{{P}}_2}} tr(\mathbf{{H}}{\mathbf{{X}}_1}{{\mathbf{{P}}}_1}{\mathbf{{P}}}_1^T\mathbf{{X}}_1^T\mathbf{{H}}{\mathbf{{X}}_2}{{\mathbf{{P}}}_2}{\mathbf{{P}}}_2^T\mathbf{{X}}_2^T)\\ &{}\;\;\;\;s{.}t.\;{\mathbf{{P}}}_1^T{{\mathbf{{P}}}_1} = {\mathbf{{I}}_1};{\mathbf{{P}}}_2^T{{\mathbf{{P}}}_2} = {\mathbf{{I}}_2}, \end{matrix}} \end{aligned}$$
(4)

where the orthogonal constraints imposed on \(\mathbf {P}_v(v=1,2)\) is to avert the trivial solution of all zeros.

As demonstrated in literatures such as [14, 21], \(\ell _{2,1}\)-norm based learning models have capabilities of sparsity, feature selection and robustness to noise. Inspired by this, by imposing the \(\ell _{2,1}\)-norm constraint on the projection matrix \({\mathbf{{P}}}_v\)(\(v=1,2)\) as regularization terms to learn more discriminative representations for multi-view data, accordingly we have the following formulation:

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{{\mathbf{{P}}_1},\;{\mathbf{{P}}_2}\;} tr\left( {\mathbf{{H}}{\mathbf{{X}}_1}{\mathbf{{P}}_1}{} \mathbf{{P}}_1^T\mathbf{{X}}_1^T\mathbf{{H}}{\mathbf{{X}}_2}{\mathbf{{P}}_2}{} \mathbf{{P}}_2^T\mathbf{{X}}_2^T} \right) - {\lambda _1}{\left\| {{\mathbf{{P}}_1}} \right\| _{2,1}} - {\lambda _2}{\left\| {{\mathbf{{P}}_2}} \right\| _{2,1}} \\ s{.}t.\;\;\mathbf{{P}}_1^T{\mathbf{{P}}_1} = {\mathbf{{I}}_1};\;\;\mathbf{{P}}_2^T{\mathbf{{P}}_2} = {\mathbf{{I}}_2}, \\ \end{array} \end{aligned}$$
(5)

where \(\lambda _1\) and \(\lambda _2\) are the regularization parameters.

3.2 Optimization

Since the optimization objective function involved the \(\ell _{2,1}\)-norm, which is an intractable problem to handle. Consequently, here we employ the alternative optimization strategy to solve the optimization problem. With \({\left\| \mathbf{{A}} \right\| _{2,1}} = tr\left( {{\mathbf{{A}}^T}{} \mathbf{{DA}}} \right) \) where \(\mathbf{{D}} = diag\left( {\frac{1}{{{{\left\| {{A^{ \cdot \cdot i}}} \right\| }_2}}}} \right) \), first let us re-express the formulation in Eq. (5) as:

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{{\mathbf{{P}}_1},\;{\mathbf{{P}}_2}} tr\left( {\mathbf{{H}}{\mathbf{{X}}_1}{\mathbf{{P}}_1}{} \mathbf{{P}}_1^T\mathbf{{X}}_1^T\mathbf{{H}}{\mathbf{{X}}_2}{\mathbf{{P}}_2}{} \mathbf{{P}}_2^T\mathbf{{X}}_2^T} \right) - {\lambda _1}tr\left( {\mathbf{{P}}_1^T{\mathbf{{D}}_1}{\mathbf{{P}}_1}} \right) - {\lambda _2}tr\left( {\mathbf{{P}}_2^T{\mathbf{{D}}_2}{\mathbf{{P}}_2}} \right) \\ s{.}t.\;\mathbf{{P}}_1^T{\mathbf{{P}}_1} = {\mathbf{{I}}_1};\;\mathbf{{P}}_2^T{\mathbf{{P}}_2} = {\mathbf{{I}}_2}. \\ \end{array} \end{aligned}$$
(6)

Specifically, according to the alternative optimization rules, the optimization problem formulated in Eq. (6) (i.e. Eq. (5)) can be decomposed into the following two sub-maximization ones:

(1) Solve \(\mathbf{{P}}_1\) , fixing \(\mathbf{{P}}_2\):

$$\begin{aligned} \begin{aligned}&\mathop {\;\;\max }\limits _{{\mathbf{{P}}_1}} tr(\mathbf{{H}}{\mathbf{{X}}_1}{\mathbf{{P}}_\mathrm{{1}}}{} \mathbf{{P}}_1^T\mathbf{{X}}_1^T\mathbf{{H}}{\mathbf{{X}}_2}{\mathbf{{P}}_2}{} \mathbf{{P}}_2^T\mathbf{{X}}_2^T) - {\lambda _1}tr\left( {\mathbf{{P}}_1^T{\mathbf{{D}}_1}{\mathbf{{P}}_1}} \right) \\ \Leftrightarrow&\;\; \mathop {\max }\limits _{{\mathbf{{P}}_1}} tr\left( {\mathbf{{P}}_1^T(\mathbf{{X}}_1^T\mathbf{{H}}{\mathbf{{X}}_2}{\mathbf{{P}}_2}{} \mathbf{{P}}_2^T\mathbf{{X}}_2^T\mathbf{{H}}{\mathbf{{X}}_1} - {\lambda _1}{\mathbf{{D}}_1}){\mathbf{{P}}_1}} \right) \\&\;\;\;s{.}t.\;\mathbf{{P}}_1^T{\mathbf{{P}}_1} = {\mathbf{{I}}_1}. \end{aligned} \end{aligned}$$
(7)

Let \({\mathbf{{B}}_1} = \mathbf{{X}}_1^T\mathbf{{H}}{\mathbf{{X}}_2}{\mathbf{{P}}_2}{} \mathbf{{P}}_2^T\mathbf{{X}}_2^T\mathbf{{H}}{\mathbf{{X}}_1} - {\lambda _1}{\mathbf{{D}}_1}\), we can obtain \(\mathbf P _1\) by solving the eigenvalue problem of \(\mathbf{{B}}_1\), here \(\mathbf P _1\) consists of the first d eigenvectors corresponding to the d largest eigenvalues of \(\mathbf{{B}}_1\).

(2) Solve \(\mathbf{{P}}_2\) , fixing \(\mathbf{{P}}_1\):

$$\begin{aligned} \begin{aligned}&\mathop {\;\;\max }\limits _{{\mathbf{{P}}_2}} tr(\mathbf{{H}}{\mathbf{{X}}_2}{\mathbf{{P}}_2}{} \mathbf{{P}}_2^T\mathbf{{X}}_2^T\mathbf{{H}}{\mathbf{{X}}_1}{\mathbf{{P}}_1}{} \mathbf{{P}}_1^T\mathbf{{X}}_1^T) - {\lambda _2}tr\left( {\mathbf{{P}}_2^T{\mathbf{{D}}_2}{\mathbf{{P}}_2}} \right) \\ \Leftrightarrow&\;\;\mathop {\max }\limits _{{\mathbf{{P}}_2}} tr\left( {\mathbf{{P}}_2^T(\mathbf{{X}}_2^T\mathbf{{H}}{\mathbf{{X}}_1}{\mathbf{{P}}_1}{} \mathbf{{P}}_1^T\mathbf{{X}}_1^T\mathbf{{H}}{\mathbf{{X}}_2} - {\lambda _2}{\mathbf{{D}}_2}){\mathbf{{P}}_2}} \right) \\&\;\;\;\;s{.}t.\;\mathbf{{P}}_2^T{\mathbf{{P}}_2} = {\mathbf{{I}}_2}. \end{aligned} \end{aligned}$$
(8)

Likewise, let \({\mathbf{{B}}_2} = \mathbf{{X}}_2^T\mathbf{{H}}{\mathbf{{X}}_1}{\mathbf{{P}}_1}{} \mathbf{{P}}_1^T\mathbf{{X}}_1^T\mathbf{{H}}{\mathbf{{X}}_2} - {\lambda _2}{\mathbf{{D}}_2}\), we can obtain \(\mathbf{{P}}_2\) by solving the eigenvalue problem of \(\mathbf{{B}}_2\), here \(\mathbf{{P}}_2\) consists of the first d eigenvectors corresponding to the d largest eigenvalues of \(\mathbf{{B}}_2\).

To better understand the procedure for solving the proposed method, we summarize in detail the solver for solving the optimization problem in Eq. (5) as Algorithm 1.

figure a

3.3 Convergence Analysis

The convergence of the proposed UDM under the iterative optimization algorithm in Algorithm 1 can be summarized by the following Theorem 1.

Theorem 1

Under the iterative optimizing rules in Algorithm 1, the objective function defined by Eq. (5) is increasing monotonically, and it can converge to its global maximum.

Due to space limitation, here we omit the detailed proof of Theorem 1. The convergence curves in Sect. 4.5 can also demonstrate the good convergence behavior of the optimizing algorithm.

4 Experiments

To test the performance of UDM, we conducted experiments on cross-modal retrieval between image and text, i.e. using image to query text (I2T) and using text to query image (T2I), adopting Mean Average Precision (MAP) as the evaluation metric and the normalized correlation (NC) as the distance measure [15].

4.1 Datasets

The follow-ups are brief descriptions on the used two datasets i.e. Wikipedia [23] and NUS-WIDE [5].

  • Wikipedia: This dataset consists of 2866 image-text pairs labeled with 10 semantic classes in total. For each image-text pair, we extract 4096-dimensional visual features by convolutional neural network to represent the image view, and 100-dimensional LDA textual features to represent the text view. In the experiment, the dataset is partitioned into two parts, one for training (2173 pairs) and the other for testing (693 pairs).

  • NUS-WIDE: This dataset is a subset from [5], including 190420 image examples totally, each with 21 possible labels. For each image-text pair, we extract 500-dimensional SIFT BoVW features for image and 1000-dimensional text annotations for text. To reduce the computational complexity, further we sample a subset with 8687 pairs of image-text. Likewise, the dataset is divided into two parts, one for training (5212 pairs) and the other for testing (3475 pairs).

4.2 Benchmark Approaches and Experimental Setup

The proposed UDM is unsupervised, kernel-based, correlation-based and sparsity-based. Accordingly, the compared approaches include CCA, KPCA [17], KCCA [16], SCCA [10]. The parameters involved in the compared approaches are kept default following the literatures. For details, please refer to the corresponding literatures. Next, we will present the specific settings for the parameters involved in UDM. First, by fixing \(\lambda _1\) and \(\lambda _2\) we determine the optimal d. Specifically, we tune d from the range of \(\{5,10,20,40,60,80\}\) and \(\{50,100,150,200,250,300,350\}\) on Wikipedia and NUS-WIDE respectively, as shown in Fig. 2. It can be seen from Fig. 2, with \(d=40\) on Wikipedia and \(d=50\) on NUS-WIDE, UDM obtains the best performance. Therefore, in the following experiments we set \(d=40\) and \(d=50\) for Wikipedia and NUS-WIDE. Then, with d fixed we decide the optimal \(\lambda _1\) and \(\lambda _2\) by tuning them from \(\{10^{-5},10^{-4},10^{-3},10^{-2},10^{-1},1,10,10^2,10^3,10^4,10^5\}\) with d fixed. Empirically, we determine \(\lambda _1=10^{-3}\) and \(\lambda _2=10^3\) on Wikipedia, as well as \(\lambda _1=\lambda _2=10^{-5}\) on NUS-WIDE. In the subsequent section, we will give the parameter sensitivity analysis on \(\lambda _1\) and \(\lambda _2\).

Fig. 2.
figure 2

MAP vs. varying d on Wikipedia and NUS-WIDE with \(\lambda _1\) and \(\lambda _2\) fixed

Full size image
Table 1. MAP comparison on Wikipedia
Full size table
Table 2. MAP comparison on NUS-WIDE
Full size table
Fig. 3.
figure 3

Per class MAP on NUS-WIDE

Full size image
Fig. 4.
figure 4

MAP vs. varying \(\lambda _1\) and \(\lambda _2\) on NUS-WIDE

Full size image
Fig. 5.
figure 5

MAP vs. varying \(\lambda _1\) and \(\lambda _2\) on Wikipedia

Full size image

4.3 Results

Tables 1 and 2 displays the comparison results on two datasets, respectively. As can be seen from Tables 1 and 2, the proposed UDM performs best, followed by KCCA, on both Wikipedia and NUS-WIDE. Besides, Fig. 3 shows the per-class MAP scores of all the compared approaches on NUS-WIDE. From Fig. 3, we can observe that UDM achieves better results on most categories, but it is not always the best on each category. More specifically, it achieves the best result on the first sixteen categories while it is the worst among the five approaches on category 20 and category 21. Therefore, incorporating label supervision information will be considered to improve UDM for each category.

4.4 Parameter Sensitivity Analysis

To show the impacts of \(\lambda _1\) and \(\lambda _2\) on UDM, we have carried out experiments on Wikipedia and NUS-WIDE respectively, by tuning them from the same range set as Subsect. 4.2. Figures 4 and 5 shows the retrieval MAP scores versus different values of \(\lambda _1\) and \(\lambda _2\) on NUS-WIDE and Wikipedia respectively. From Figs. 4 and 5, we can see that the performance of UDM varies as \(\lambda _1\) and \(\lambda _2\) changes. By contrast, the proposed UDM on Wikipedia is much more sensitive to two parameters than on NUS-WIDE.

4.5 Convergence Study

Figure 6 displays the relationship between the objective function and the number of iteration on Wikipedia and NUS-WIDE, respectively. As can be observed from Fig. 6, for each dataset, the objective function defined in Eq. (5) can rapidly converge to its maximum within about ten iterations, which demonstrates the efficiency of the designed iterative optimization algorithm.

Fig. 6.
figure 6

The objective function vs. the number of iteration

Full size image

5 Conclusions and Future Work

In this paper, we have proposed a HSIC-based unsupervised learning approach for discovering common subspace representations shared by multi-view data, which is a kernel-based, correlation-based and sparsity-based projection method. To solve the optimization problem, we develop an efficient iterative optimizing algorithm. Cross-modal retrieval results on two benchmark datasets have shown the superiority of the proposed UDM over the compared approaches. Inspired by CCA-like methods, nonlinear extensions of UDM will be considered by incorporating nonlinear kernel and neutral network to expect a better common representation for multi-view data in future work.