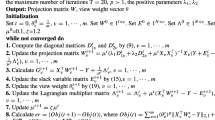Structured Multi-view Supervised Feature Selection Algorithm Research

Abstract

Face more and more multi-view data, how to enhance the feature selection performance has become one of the research issues. However, the most existing multi-view feature selection methods only consider the importance of each view features, but ignore the importance of individual feature in each view in the feature selection progress. In this paper we propose a novel supervised feature selection method based on structured multi-view sparse regularization, namely Structured Multi-view Supervised Feature Selection (SMSFS). SMSFS can realize feature selection by both considering the importance of each view features and the importance of individual feature in each view to boost the feature selection performance. Extensive experiments are performed on two image datasets and the results show the effectiveness of the proposed method SMSFS.

1 Introduction

Recently, with the rapid development of the information technology and computer vision technology, image and video data are often expressed by a lot of different types of visual features, such as the shape, the color, the texture, etc. Each type of features characterizes these data in one specific feature space and has particular physical meaning and statistic property. Conventionally, each type can be regarded as a view and the data represented by different types of features is named as multi-view data [1]. However, these abundant and various types of features not only result in high computational cost, but also often comprise irrelevant and/or redundant features. Therefore, feature selection, as a process of selecting relevant features and reducing dimensionality, has become a research issue. However, confronting with multi-view data, the conditional single-view feature selection methods havent d good feature selection performance. So some multi-view feature selection methods have been widely researched and proposed in recent years. One of the methods is to directly concatenate the multi-view features into a long vector, and then single-view methods are adopted to realize the feature selection [2, 3]. This concatenation strategy is easy to realized, but it cannot efficiently explore the complementary of different view features.

Recently, multi-view learning has been widely applied into the feature selection methods to enhance the feature selection performance by exploring the correlated and complemental information between different views [1, 4]. However, these methods consider one view features as a whole and all features in the same view have equally importance, ignoring the importance of individual feature in each view. If we can not only consider the importance of each view features, but also consider the importance of individual feature in each view in the feature selection progress, the feature selection performance can be enhanced. In [5], Wang et al. have proposed group $\ell$1-norm (G1-norm), which can discriminate different importance of the features of a specific view. In [6], Wang et al. have proposed a sparse multimodal learning approach to integrate heterogeneous features by using the joint structured sparsity regularizations.

In this paper, we propose a new structured multi-view supervised feature selection framework, namely Structured Multi-view Supervised Feature Selection (SMSFS). SMSFS can enhance the feature selection performance by considering the importance of each view features without ignoring the importance of individual feature in each view based on structured multi-view sparse regularization. SMSFS is applied into image annotation task on two image datasets, NUS-WIDE [7] and MSRA MM 2.0 [8], and the experimental results demonstrate that effectiveness of the proposed algorithm.

2 Related Work

In this section, we discuss two related works on multi-view learning and sparse regularization.

2.1 Multi-view Learning

Recently, multi-view learning has obtained extensive research interest and different types of multi-view learning algorithms have been proposed. These algorithms can be roughly classified four kinds: co-training [9], subspace learning-based algorithm, multiple kernel learning (MKL) and graph ensemble-based multi-view learning.

Co-training [9] trains alternately to maximize the mutual agreement on two distinct different views of data and it can improve the performance when the two views are conditionally independent of each other. Subspace learning-based algorithm aims to obtain a latent subspace shared by multiple views by assuming that the input views are generated from this latent subspace. The representative algorithms include canonical correlation analysis (CCA) [10] and kernel canonical correlation analysis (KCCA) [11]. Multiple kernel learning learns a kernel machine from multiple Gram kernel matrices [12], which naturally correspond to different views of features and are combined either linearly or non-linearly to improve learning performance. Graph ensemble-based algorithms integrate multiple graphs, each of which encodes the local geometry of a particular view, to explore complementary properties of different views [1].

2.2 Sparse Regularization

In order to select the most discriminative features, a variety of sparse regularization has been widely applied into feature selection, including $l_1$-norm (LASSO), $l_p$-norm ($0<p\le 1$), $l_{2,1}$-norm and $l_{2,p}$-matrix norm ($0<p\le 1$). Though $l_1$-norm (LASSO) [13] is the most well-known sparse regularization, it has not good sparsity. In order to obtain better sparsity, much works [14, 15] have extended the $l_1$-norm to the $l_p$-norm ($0<p<1$) model. In [16], Xu et al. have concluded that when p is $1{\slash }2$, the $l_p$-norm, i.e. $l_{1/2}$-norm has the best sparsity. In [17], Nie et al. have introduced a joint $l_{2,1}$-norm minimization on both loss function and regularization for feature selection. In [18], Wang et al. have extended $l_{2,1}$-norm to $l_{2,p}$-matrix norm ($0<p\le 1$) to select joint and more sparse features. When p is equal to $1{\slash }2$, the $l_{2,1/2}$-norm has the best performance.

3 Structured Multi-view Supervised Feature Selection (SMSFS)

In this section, we propose a novel structured multi-view supervised feature selection framework SMSFS. We introduce the SMSFS formulation, and then conduct an effective algorithm for optimizing the objective function.

3.1 SMSFS Formulation

3.1.1 Structured Multi-view Sparse Regularization

Let $W\in \mathbb {R}^{d\times c}$ be the projection matrix, and then W can be expressed as:

$$\begin{aligned} W= \left[ \begin{array}{ccc} w_1^1 &{} \cdots &{} w_c^1\\ \cdots &{} \cdots &{} \cdots \\ w_1^m&{}\cdots &{}w_c^m\\ \end{array} \right] \in \mathbb {R}^{d\times c} \end{aligned}$$

(1)

where $W_p^q\in \mathbb {R}^{d_q}$ indicates the weights of all features in the q-th view with respect to the p-th class.

The $l_{2,1/2}$-matrix norm of the projection matrix $W\in \mathbb {R}^{d\times c}$ is defined as [18]:

$$\begin{aligned} ||W||_{2,1/2}=(\sum _{i=1}^d||w_i||_2^{1/2})^2 \end{aligned}$$

(2)

The group $l_1$-norm ($G_1$-norm) is defined as [5]:

$$\begin{aligned} ||W||_{G1}=\sum _{i=1}^c\sum _{j=1}^m||w_i^j||_2 \end{aligned}$$

(3)

Therefore, the structured multi-view sparse regularization is constructed with the group $l_1$-norm ($G_1$-norm) and $l_{2,1/2}$-matrix norm in our proposed algorithm SMSFS.

$$\begin{aligned} ||W||_{G1}+\mu ||W||_{2,1/2}^{1/2} \end{aligned}$$

(4)

This structured multi-view sparse regularization can guarantee the proposed algorithm SMSFS realize feature selection by considering both the importance of each view features and the importance of individual feature in each view. Then the feature selection performance can be boosted.

3.1.2 SMSFS Formulation

The multi-view training data are denoted as $X=[x_1,x_2\cdots ,x_n]^T$ and the ith multi-view datum with m views is denoted as $x_i=[x_i^1,x_i^2\cdots ,x_i^m]^T\in \mathbb {R}^{(\sum _{v=1}^m d_v)\times 1}$. Thus, the feature data matrix of vth view and the feature matrix of all views can be denoted as $X^v=[x_1^v,x_2^v\cdots ,x_n^v]\in \mathbb {R}^{d_v\times n}$ and $X=[X^1,X^2,\cdots ,X^m]^T\in \mathbb {R}^{d\times n}$ respectively, where $d=\sum _{v=1}^m d_v$. $Y=[y_1,y_2\cdots ,y_n]^T\in {0,1}^{n\times c}$ is the label of training dataset, where c is the number of classes and $y_i \in \mathbb {R}^{l\times c}(1\le i\le n)$ is the ith label vector.

A generally sparse feature selection framework to obtain W is to minimize the following regularized empirical error

$$\begin{aligned} min_W loss(W^TX,Y)+\lambda R(W) \end{aligned}$$

(5)

where $loss(\cdot )$ is the loss function and $\lambda R(W)$ is the regularization with $\lambda$ as its regularization parameter.

Here we select the minimizing the prediction error as the loss function and the structured multi-view sparse regularization as the regularization, then the proposed SMSFS can be presented as follows:

$$\begin{aligned} argmin_W ||X^TW-Y||_F^2+\lambda ||W||_{G1}+\mu ||W||_{2,1/2}^{1/2} \end{aligned}$$

(6)

where $\lambda ||W||_{G1}+\mu ||W||_{2,1/2}^{1/2}$ is the structured multi-view sparse regularization-which guarantees SMSFS consider both the importance of each view features and the importance of individual feature in each view, and then achieve good feature selection performance. $\lambda$ and $\mu$ are regularization parameters. $||X^TW-Y||_F^2$ is the loss function.

3.2 Optimization

Because the $l_{2,1/2}$-matrix norm is non-convex and $G_1$-norm is non-smooth, we propose an efficient algorithm to solve the objective function (6) in this section.

Given $W=[w^1,\cdots ,w^d]^T$ and define a diagonal matrix $\widetilde{D}$ with diagonal elements $\widetilde{D}_{ii}=1/4||w^i||^{3/2}$ then we can get $||W||_{2,1/2}^{1/2}=4Tr(W^T\widetilde{D}W)$ and $||W||_{G1}=\sum _{i=1}^c\sum _{j=1}^k||w_i^j||_2$.

So the objective function in (6) can be written as:

$$\begin{aligned} \begin{aligned}&argmin_W Tr((X^TW-Y)^T(X^TW-Y))\\&\qquad +\lambda \sum _{i=1}^cTr(w_i^TD^iw_i)+\mu Tr(W^T\widetilde{D}W) \end{aligned} \end{aligned}$$

(7)

By setting the derivative of (7) w.r.t to zero, we have

$$\begin{aligned} X(X^Tw_i-y_i)+\lambda D^iw_i+4\mu \widetilde{D}w_i=0 \end{aligned}$$

(8)

where $D^i(1\le i\le c)$ is a block diagonal matrix with the j-th diagonal block as $\frac{1}{2||w_i^j||_2}I_j$ $I_j$ is an identity matrix with size of $d_j$.

Therefore, we can obtain

$$\begin{aligned}&X(X^Tw_i-y_i)+\lambda D^iw_i+4\mu \widetilde{D}w_i=0\nonumber \\&w_i=(XX^T+\lambda D^i+4\mu \widetilde{D})^{-1}Xy_i \end{aligned}$$

(9)

An iterative algorithm is proposed to solve the objective function in Algorithm 1.

Algorithm 1. The SMSFS algorithm.

Input: The vth view feature matrix $X^v\in \mathbb {R}^{d_v\times n}$ and the feature matrix $X\in \mathbb {R}^{d\times n}$; The labels matrix $Y\in \mathbb {R}^{n\times c}$; Regularization parameters $\lambda ,\mu$.

1: Initialize projected matrix $W_0 \in \mathbb {R}^{d\times c}$ randomly;

2: repeat

Compute the diagonal matrix $\widetilde{D}_t=\left[ \begin{array}{ccc} \frac{1}{4||w_t^1||_2^{3/2}} &{} &{}\\ &{} \cdots &{} \\ &{}&{}\frac{1}{4||w_t^d||_2^{3/2}}\\ \end{array} \right]$;

Compute the block diagonal matrix $D^i_t(1\le i\le c)$ where the j-th diagonal block $\frac{1}{2||w_i^j||_2}I_j$;

For each $w_i(1\le i\le c), (w_t)_i=(XX^+\lambda D_t^i+4\mu \widetilde{D}_t)^{-1}Xy_i$

$t=t+1;$

until convergence;

Output: Optimized projected matrix $W\in \mathbb {R}^{d\times c}$.

4 Experiments

In our paper, we apply the proposed algorithm SMSFS into image annotation task on two image datasets NUS-WIDE dataset [7] and MSRA-MM2.0 dataset [8].

4.1 Datasets and Visual Features

NUS-WIDE dataset includes 269648 real-world images belonging to 81 concepts and MSRA-MM2.0 dataset consists of 50000 images belonging to 100 concepts. In our experiments, we use three types of visual features, including 144-dimension color correlogram, 128-dimension wavelet texture and 73-dimension edge direction histogram for NUS-WIDE dataset or 75-dimension edge direction histogram for MSRA-MM 2.0 dataset.

4.2 Experiment Setup

In our experiments, we randomly sample 3000 images as training data in each dataset. The experiments are independently repeated five times with the average results. The regularization parameters $\mu$ and $\lambda$ in objective function (6) are tuned from 0.00001, 0.001, 0.1, 1, 10, 1000, 100000 and the best results are reported.

We compare our proposed method SMSFS with two supervised feature selection methods, including sub-feature uncovering with sparsity (SFUS) [3] and sparse multimodal learning method by utilizing mixed structured sparsity norms (SMML) [6]. To evaluate the performance, three evaluation metrics, i.e., Mean Average Precision (MAP), MicroAUC and MacroAUC are used in our experiments.

4.3 Performance Evaluation

We compare the proposed method SMSFS with SFUS and SMML on two datasets, and the compared results are listed in Table 1. The best results are shown in bold.

Table 1. Performance comparison

From Table 1, we can see that SMSFS has better performance than SFUS and SMML in term of MAP, MacroAUC and MicroAUC on two datasets. This indicates that SMSFS can utilize the structured multi-view sparse regularization to select the most discriminative features, and then to boost the image annotation performance.

4.4 Influence of Selected Features

Here we conduct an experiment to study the performance variation with different selected features number. At the same time, we compare the proposed method SMSFS with SMML and SFUS. The number of selected features is set to 100, 150, 200, 250, 300, and all for NUS-WIDE dataset and MSRA-MM2.0 dataset respectively. MAP is used as the metric and the results of this experiment are shown in Fig. 1.

Fig. 1.

The performance variation according to the number of selected features of methods SMSFS, compared with SMML and SFUS. (a) NUS-WIDE dataset. (b) MSRA-MM dataset.

Fig. 2.

MAP variation according to $\mu$ and $\lambda$ on different datasets. (a) NUS-WIDE dataset. (b) MSRA dataset.

Figure 1 illustrates that the performance of SMSFS, SFUS and SMML varies when the number of selected features changes. From Fig. 1 we can see: (1) When the number of selected features is too small, MAP is lower than that with all features. This could be attributed to the loss of some useful information. (2) When all the features are selected, MAP is not the best because some noise is included in the initial visual features. (3) Three methods all have the largest MAP with 250 selected features on two datasets, but MAP of SMSFS is higher than those of SFUS and SMML. These results indicate that the proposed method SMSFS can select the more sparse and discriminative features to achieve the good performance based on the structured multi-view sparse regularization.

4.5 Regularization Parameters Analysis

There are two regularization parameters $\mu$ and $\lambda$ in SMSFS objective function (6). In this section, we use “grid-search” strategy from 0.00001, 0.001, 0.1, 1, 10, 1000, 100000 to learn the parameter sensitivity. Here MAP is used as the metric and Fig. 2 demonstrates the MAP variation with $\mu$ and $\lambda$ on two datasets.

From Fig. 2 we obtain that the performance of SMSFS is sensitive to regularization parameters $\mu$ and $\lambda$. SMSFS can obtain the largest MAP by setting $\mu$ to 10 and $\lambda$ to 1000 on NUS-WIDE dataset, and obtain the largest MAP by setting $\mu$ to 10 and $\lambda$ to 10 on MSRA dataset respectively.

5 Conclusion

In this paper we propose a novel structured multi-view supervised feature selection framework SMSFS, which can enhance the performance of feature selection by considering both the importance of features of each view and the importance of each feature of one view based on the structured multi-view sparse regularization. Because the objective function of SMSFS is non-convex, we introduce an effective algorithm for optimizing the objective function. Some experiments are conducted on two datasets for image annotation task and the results demonstrate that proposed algorithm SMSFS can achieve good feature selection performance.