A Low-Rank Total-Variation Regularized Tensor Completion Algorithm

Abstract

In this paper, we first model visual data as a tensor and then impose both low-rank and total-variation constraint to complete the tensor. More specifically, we adopt a novel tensor-tensor production framework (also known as t-product) and its theory of low-rank based completion. By using the concept of t-product, it is the first time that we extend classic Total-Variation (TV) to a t-product and $l_{1,1,2}$ norm based constraint on the gradient of visual data. After proposing our model, we derive a iterative solver based on alternating direction method of multipliers (ADMM). We show the effectiveness of our method and compare our method with state-of-art algorithms in the experimental section.

1 Introduction

Recent years has witnessed the development of acquisition techniques, and the visual data tends to contain more and more information and thus should be treated as a complex high-dimensional data, i.e. tensors. For example, a hyperspectral image or multispectral image can be represented as a third-order tensor since the spatial information has two dimensions and the spectral information takes one dimension. Using a tensor to model visual data can handle the complex structure better and has become a hot topic in computer vision community recently, for instance, face recognition [15], color image and video in-painting [7], hyperspectral image processing [16, 17], gait recognition [12].

Visual data may have missing values in the acquisition process due to mechanical failure or man-induced factors. If we process the multi-way array data as a tensor instead of splitting it into matrices, estimating missing values for visual data is also known as tensor completion problem. Motivated by the successful achievements of low-rank matrix completion methods [8, 10], many tensor completion problems could also be solved through imposing low-rank constraint. Decomposition and subspace methods has been widely studied [13, 14] and a common way to impose low-rank constraint is to decompose tensors and get its factors first, then by limiting the sizes of factors we attain low-rank property. CP decomposition and Tucker decomposition are two classic decomposition methods to compute the factors of a tensor [5]. However, both the two methods mentioned above have crucial parameters that are supposed to be determined by users. In this paper, we adopt a novel tensor-tensor product framework [1], and a singular value decomposition formula for tensors [3, 4], which is parameter-free. The rencently proposed singular value decomposition formula for tensors is also referred to as t-SVD, and t-SVD has been proved effective by many influential papers [18].

When trying to restore degraded visual data, it is reasonable to utilize the local smoothness property of visual data as prior knowledge or regularization. A common constraint is Total-Variation (TV) norm, which is computed as the $l_1$ of the gradient magnitude, and this norm has been qualified to be effective to preserve edges and piecewise structures. If we take the low-rank assumption as a global constraint and TV norm as a local prior, then it is natural to combine this two constraints together to estimate missing values in visual data. So more recently, some related methods that take tensor and TV into consideration are proposed [2, 6, 11]. [2] aims to design a norm that considers both the inhomogeneity and the multi-directionality of responses to derivative-like filters. [11] proposes an image super-resolution method that integrates both low-rank matrix completion and TV regularization. [6] proposes integrating TV into low-rank tensor completion, but their methods use the same rank definition as [7] or Tucker decomposition, and as mentioned before, the parameters are hard to deal with. Moreover, TV is $l_1$ norm on matrix but we are processing visual tensors, so we need to extend TV to tensor cases. Also, we employ a new tensor norm namely $l_{1,1,2}$ which stems from multi-task learning [9].

In this paper, we seek to design a parameter-free method for low-rank based completion procedure, which means parameters only exist in TV regularization. To achieve this goal, simply using t-SVD framework is not enough, since t-SVD is based on t-product and a free module so we need to reinvent TV with t-product system. Our main contributions are as follows:

• 1. Using the concept of t-product, we design difference tensors $\mathcal {A}$ and $\mathcal {B}$ that when multiplied by a visual tensor $\mathcal {X}$ takes the gradient of $\mathcal {X}$, i.e. $\nabla \mathcal {X}$.

• 2. Motivated by $l_{1,1,2}$ norm which is originally designed to model sparse noise in visual data [18], we use $l_{1,1,2}$ norm to ensure sparsity of the gradient magnitude, then traditional TV is extended to tensor cases.

2 Notations and Preliminaries

In this section, we introduce some notations of tensor algebra and give the basic definitions used in the rest of the paper.

Scalars are denoted by lowercase letters, e.g., a. Vectors are denoted by boldface lowercase letters, e.g., $\mathbf {a}$. Matrices are denoted by capital letters, e.g., A. Higher-order tensors are denoted by boldface Euler script letters, e.g., $\mathcal {A}$. For a third-order tensor $\mathcal {A}\in \mathbb {R}^{r \times s\times t}$, the ith frontal slice is denoted $A_i$. In terms of MATLAB indexing notation, we have $A_i = \mathcal {A}(:,:,i)$.

The definition of new tensor multiplication strategy [1] begins with converting $\mathcal {A}\in \mathbb {R}^{r \times s\times t}$ into a block circulant matrix. Then

$$ {\texttt {bcirc}}(\mathcal {A}) = \begin{pmatrix} A_1 &{} A_n &{} A_{n-1} &{} \cdots &{} A_{2} \\ A_{2} &{} A_1 &{} A_n &{} \cdots &{} A_{3} \\ A_{3} &{} A_{2} &{} A_1 &{} \cdots &{} A_{4} \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ A_n &{} A_{n-1} &{} A_{n-2} &{} \cdots &{} A_1 \end{pmatrix} $$

is a block circulant matrix of size $rt\times st$. And the ${\texttt {unfold}}$ command rearrange the frontal slices of $\mathcal {A}$:

$$ {\texttt {unfold}}(\mathcal {A}) = \begin{pmatrix} A_1 \\ A_2 \\ \vdots \\ A_n \end{pmatrix}, \quad {\texttt {fold}}({\texttt {unfold}}(\mathcal {A})) = \mathcal {A}$$

Then we have the following new definition of tensor-tensor multiplication.

Definition 1

(t-product). Let $\mathcal {A}\in \mathbb {R}^{r \times s\times t}$ and $\mathcal {B}\in \mathbb {R}^{s \times p\times t}$. Then the t-product $\mathcal {A}*\mathcal {B}$ is a $r \times p\times t$ tensor

$$\begin{aligned} \mathcal {A}*\mathcal {B}= {\texttt {fold}} ({\texttt {bcirc}} (\mathcal {A}) \cdot {\texttt {unfold}} (\mathcal {B})) \end{aligned}$$

(1)

An important property of the block circulant matrix is the observation that a block circulant matrix can be block diagonalized in the Fourier domain [3]. Before moving on to the definition of t-SVD, we need some more definitions from [4].

Definition 2

(Tensor Transpose). Let $\mathcal {A}\in \mathbb {R}^{r \times s\times t}$, then $\mathcal {A}^T\in \mathbb {R}^{s \times r\times t}$ and

$$ \mathcal {A}^T = {\texttt {fold}} ([A_1, A_n, A_{n-1}, \cdots , A_2]^T) $$

Definition 3

(Identity Tensor). The identity tensor $\mathcal {I}\in \mathbb {R}^{m \times m\times n}$ is the tensor whose first frontal slice is the $m\times m$ identity matrix, and whose other frontal slices are all zeros.

Definition 4

(Orthogonal Tensor). A tensor $\mathcal {Q}\in \mathbb {R}^{m \times m\times n}$ is orthogonal if $\mathcal {Q}^T*\mathcal {Q}=\mathcal {Q}*\mathcal {Q}^T=\mathcal {I}$.

Definition 5

(f-diagonal Tensor). A tensor is called f-diagonal if each of its frontal slices is a diagonal matrix.

Definition 6

(Inverse Tensor). A tensor $\mathcal {A}\in \mathbb {R}^{m \times m\times n}$ has an inverse tensor $\mathcal {B}$ if

$$ \mathcal {A}*\mathcal {B}= \mathcal {I}\quad \text {and} \quad \mathcal {B}*\mathcal {A}= \mathcal {I}$$

Using these new definitions, we are able to derive a new decomposition method named t-SVD and an approximation theorem on this decomposition.

Theorem 1

(t-SVD). Let $\mathcal {A}\in \mathbb {R}^{r \times s\times t}$, then the t-SVD of $\mathcal {A}$ is

$$\begin{aligned} \mathcal {A}= \mathcal {U}*\mathcal {S}*\mathcal {V}^T \end{aligned}$$

(2)

where $\mathcal {U}\in \mathbb {R}^{r\times r\times t}$, $\mathcal {V}\in \mathbb {R}^{s\times s\times t}$ are orthogonal and $\mathcal {S}\in \mathbb {R}^{r\times s\times t}$ is f-diagonal.

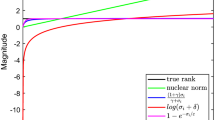
By using the idea of computing in the Fourier domain, we can efficiently compute the t-SVD factorization, and for more details see [3, 4]. Then nuclear norm for $\mathcal {A}$ is defined as $\Vert \mathcal {A}\Vert _* = \sum _{j=1}^t\sum _{i=1}^{\min (r,s)} |\hat{\mathcal {S}}(i,i,k)|$, where $\hat{\mathcal {S}}$ is the result of taking the Fourier transform along the third dimension of $\mathcal {S}$.

3 Proposed t-SVD-TV

In this section, we will first give the details of our model, and then derive a solver with alternating direction method of multipliers (ADMM). Since we combine t-SVD and TV together, we name our method as t-SVD-TV.

3.1 Low-Rank Regularization

Before discussing low-rank model, we need some notations for our problem first. Suppose there is a tensor $\mathcal {M}\in \mathbb {R}^{n_1\times n_2\times n_3}$ representing some visual data with missing entries, and we use $\varOmega$ indicating the set of indices of observations, $\mathcal {X}$ denoting the desired recovery result, then we have

$$ \mathcal {P}_\varOmega (\mathcal {X}) = \mathcal {P}_\varOmega (\mathcal {M}) $$

where $\mathcal {P}_\varOmega ()$ is the projector onto the known indices $\varOmega$. So we have the following vanila model [18]:

$$\begin{aligned} \begin{aligned} \min _{\mathcal {X}}&\quad \Vert \mathcal {X}\Vert _* \\ \text {s.t.}&\quad \mathcal {P}_\varOmega (\mathcal {X}) = \mathcal {P}_\varOmega (\mathcal {M}) \end{aligned} \end{aligned}$$

(3)

Our method takes both low-rank and TV into consideration, which means we also have terms to ensure sparsity on gradient field. We use $\varPsi (\cdot )$ as a function promoting sparsity, so our model is

$$\begin{aligned} \begin{aligned} \min _{\mathcal {X}}&\quad \Vert \mathcal {X}\Vert _* + \lambda _1\varPsi \left( \frac{\partial }{\partial _x}\mathcal {X}\right) + \lambda _2\varPsi \left( \frac{\partial }{\partial _y}\mathcal {X}\right) \\ \text {s.t.}&\quad \mathcal {P}_\varOmega (\mathcal {X}) = \mathcal {P}_\varOmega (\mathcal {M}) \end{aligned} \end{aligned}$$

(4)

where $\lambda _1, \lambda _2$ are tunable parameters. The forms of $\frac{\partial }{\partial _x}\mathcal {X}$, $\frac{\partial }{\partial _y}\mathcal {X}$ and $\varPsi (\cdot )$ are given in the following texts.

3.2 TV Regularization

When we need to compute the gradient matrix of a 2D image M, a common way is to design a difference matrix A, B. If we assume vertical direction is x and horizontal direction is y, then from AM we get $\frac{\partial }{\partial _x}M$ and from MB we get $\frac{\partial }{\partial _y}M$. And for a 3D data $\mathcal {X}$ we can derive similar means implemented by t-product system. Without loss of generality, we assume $\mathcal {X}\in \mathbb {R}^{n\times n \times k}$. By extending difference matrices to tensors, we define a difference tensor as follows:

$$ \mathcal {A}={\texttt {fold}}\begin{pmatrix}A \\ 0 \\ 0\end{pmatrix} \quad \text {and}\quad \mathcal {B}={\texttt {fold}}\begin{pmatrix}B \\ 0 \\ 0\end{pmatrix} $$

where A and B are $n\times n$ difference matrix:

$$ A=\frac{1}{2} \begin{pmatrix} -2 &{} 2 &{} 0 &{} \cdots &{} 0 &{} 0 \\ -1 &{} 0 &{} 1 &{} \cdots &{} 0 &{} 0\\ 0 &{} -1 &{} 0 &{} \cdots &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} \cdots &{} -2 &{} 2 \end{pmatrix} \quad \text {and}\quad B=\frac{1}{2} \begin{pmatrix} -2 &{} -1 &{} 0 &{} \cdots &{} 0 &{} 0 \\ 2 &{} 0 &{} -1 &{} \cdots &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} \cdots &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} -2 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 &{} 2 \end{pmatrix} $$

For a visual tensor $\mathcal {X}$, we get its gradient tensor by multiplying with $\mathcal {A}, \mathcal {B}$

$$\begin{aligned} \frac{\partial }{\partial _x}\mathcal {X}=\mathcal {A}*\mathcal {X},\quad \frac{\partial }{\partial _y}\mathcal {X}=\mathcal {X}*\mathcal {B}\end{aligned}$$

(5)

Note that $\mathcal {A}*\mathcal {X}, \mathcal {X}*\mathcal {B}$ are third order tensors which have the same size as $\mathcal {X}$. In order to promote sparsity of the gradient, we use the $l_{1,1,2}$ norm for 3D tensors as penalty function $\varPsi (\cdot )$. $l_{1,1,2}$ norm is introduced in [18] to model the sparse noise, and for a third order tensor $\mathcal {G}$, $\Vert \mathcal {G}\Vert _{1,1,2}$ is defined as $\sum _{i,j} \Vert \mathcal {G}(i,j,:)\Vert _F$. Then our optimization problem (4) becomes

$$\begin{aligned} \begin{aligned} \min _{\mathcal {X}}&\quad \Vert \mathcal {X}\Vert _* + \lambda _1 \Vert \mathcal {A}*\mathcal {X}\Vert _{1,1,2} + \lambda _2 \Vert \mathcal {X}*\mathcal {B}\Vert _{1,1,2} \\ \text {s.t.}&\quad \mathcal {P}_\varOmega (\mathcal {X}) = \mathcal {P}_\varOmega (\mathcal {M}) \end{aligned} \end{aligned}$$

(6)

The terms in (6) are interdependent, so we adopt a widely used splitting scheme which is known as ADMM.

3.3 Optimization by ADMM

The first step of applying ADMM is introducing auxiliary variables. Specifically, let $\mathcal {S}, \mathcal {Y}, \mathcal {Z}_1, \mathcal {Z}_2$ have the same size as $\mathcal {X}$, then our optimization problem (6) becomes

$$\begin{aligned} \begin{aligned} \min _{\mathcal {X}}&\quad \Vert \mathcal {S}\Vert _* + \lambda _1 \Vert \mathcal {Y}_1\Vert _{1,1,2} + \lambda _2 \Vert \mathcal {Y}_2\Vert _{1,1,2} \\ \text {s.t.}&\quad \mathcal {Y}_1 = \mathcal {A}*\mathcal {Z}_1, \mathcal {Y}_2 = \mathcal {Z}_2*\mathcal {B}\\&\quad \mathcal {S}= \mathcal {X}, \mathcal {Z}_1=\mathcal {X}, \mathcal {Z}_2 = \mathcal {X},\\&\quad \mathcal {P}_\varOmega (\mathcal {X}) = \mathcal {P}_\varOmega (\mathcal {M}) \end{aligned} \end{aligned}$$

(7)

So the augmented Lagrangian is

$$\begin{aligned} \begin{aligned} \mathcal {L}&=\Vert \mathcal {S}\Vert _* + \frac{\rho _1}{2} \left\| \mathcal {S}-\mathcal {X}+\frac{\mathcal {U}}{\rho _1}\right\| _F^2 \\&\quad + \lambda _1 \Vert \mathcal {Y}_1\Vert _{1,1,2} + \frac{\rho _2}{2} \left\| \mathcal {Y}_1 - \mathcal {A}*\mathcal {Z}_1 + \frac{\mathcal {V}_1}{\rho _2}\right\| _F^2 \\&\quad + \lambda _2 \Vert \mathcal {Y}_2\Vert _{1,1,2} + \frac{\rho _3}{2} \left\| \mathcal {Y}_2 - \mathcal {Z}_2*\mathcal {B}+ \frac{\mathcal {V}_2}{\rho _3}\right\| _F^2 \\&\quad + \frac{\rho _4}{2} \left\| \mathcal {Z}_1-\mathcal {X}+\frac{\mathcal {W}_1}{\rho _4}\right\| _F^2 + \frac{\rho _5}{2} \left\| \mathcal {Z}_2-\mathcal {X}+\frac{\mathcal {W}_2}{\rho _5}\right\| _F^2 \\ \text {s.t.}&\quad \mathcal {P}_\varOmega (\mathcal {X}) = \mathcal {P}_\varOmega (\mathcal {M}) \end{aligned} \end{aligned}$$

(8)

where tensors $\mathcal {U}, \mathcal {V}_1, \mathcal {V}_2, \mathcal {W}_1, \mathcal {W}_2$ are Lagrange multipliers and $\rho _i (i=1,...,5)$ are positive numbers. We solve (8) by alternatively minimize each variable, so (8) are turned into several subproblems:

Computing $\varvec{\mathcal {S}}$ . The subproblem for minimize $\mathcal {S}$ is

$$\begin{aligned} \mathcal {S}^{k+1} = \mathop {\mathrm{arg\,min}}\limits _\mathcal {S}\Vert \mathcal {S}\Vert _* + \frac{\rho _1}{2} \left\| \mathcal {S}-\mathcal {X}^k+\frac{\mathcal {U}^k}{\rho _1}\right\| _F^2 \end{aligned}$$

(9)

Note that (9) can be solved by the singular value thresholding method in [18], so

$$\begin{aligned} \mathcal {S}^{k+1} := \mathop {\mathrm{arg\,min}}\limits _\mathcal {S}\Vert \mathcal {S}\Vert _* + \frac{\rho _1}{2} \left\| \mathcal {S}-\mathcal {X}^k+\frac{\mathcal {U}^k}{\rho _1}\right\| _F^2 \end{aligned}$$

(10)

Computing $\varvec{\mathcal {Y}}_\mathbf{1}$ and $\varvec{\mathcal {Y}}_\mathbf{2}$ . The subproblem for minimize $\mathcal {Y}_1$ is

$$\begin{aligned} \mathcal {Y}_1^{k+1} = \mathop {\mathrm{arg\,min}}\limits _{\mathcal {Y}_1} \lambda _1 \Vert \mathcal {Y}_1\Vert _{1,1,2} + \frac{\rho _2}{2} \left\| \mathcal {Y}_1 - \mathcal {A}*\mathcal {Z}_1^k + \frac{\mathcal {V}_1^k}{\rho _2}\right\| _F^2 \end{aligned}$$

(11)

The closed form solution to (11) is given by

$$\begin{aligned} \mathcal {Y}_1^{k+1} := \left( 1-\frac{\lambda _1}{\rho _2} \left\| \mathcal {A}*\mathcal {Z}_1^k + \frac{\mathcal {V}_1^k}{\rho _2}\right\| _F^{-1} \right) _+ \left( \mathcal {A}*\mathcal {Z}_1^k + \frac{\mathcal {V}_1^k}{\rho _2}\right) \end{aligned}$$

(12)

where $(x)_+ = \max (x,0)$. Updating strategy for $\mathcal {Y}_2$ is similar to $\mathcal {Y}_1$, so

$$\begin{aligned} \mathcal {Y}_2^{k+1} := \left( 1-\frac{\lambda _2}{\rho _3} \left\| \mathcal {A}*\mathcal {Z}_1^k + \frac{\mathcal {V}_1^k}{\rho _3}\right\| _F^{-1} \right) _+ \left( \mathcal {Z}_2^k*\mathcal {B}+ \frac{\mathcal {V}_2^k}{\rho _3}\right) \end{aligned}$$

(13)

Computing $\varvec{\mathcal {Z}}_\mathbf{1}$ and $\varvec{\mathcal {Z}}_\mathbf{2}$ . The subproblem for minimize $\mathcal {Z}_1$ is

$$\begin{aligned} \mathcal {Z}_1^{k+1} = \mathop {\mathrm{arg\,min}}\limits _{\mathcal {Z}_1} \frac{\rho _2}{2} \left\| \mathcal {Y}_1^k - \mathcal {A}*\mathcal {Z}_1 + \frac{\mathcal {V}_1^k}{\rho _2}\right\| _F^2 + \frac{\rho _4}{2} \left\| \mathcal {Z}_1-\mathcal {X}+\frac{\mathcal {W}_1^k}{\rho _2}\right\| _F^2 \end{aligned}$$

(14)

Then Update $\mathcal {Z}_1$ and $\mathcal {Z}_2$ by

$$\begin{aligned} \mathcal {Z}_1^{k+1} := (\rho _4\mathcal {I}+\rho _2\mathcal {A}^T*\mathcal {A})^{-1}*\left( \rho _4\mathcal {I}-\mathcal {W}_1^k+\rho _2\mathcal {A}^T*\mathcal {Y}_1^k+\mathcal {A}^T*\mathcal {V}_1^k\right) \end{aligned}$$

(15)

Similarly, we have update rules for $\mathcal {Z}_2$:

$$\begin{aligned} \mathcal {Z}_2^{k+1} := \left( \rho _5\mathcal {I}-\mathcal {W}_2+\rho _3\mathcal {Y}_2^k*\mathcal {B}^T+\mathcal {V}_2^k*\mathcal {B}^T\right) *(\rho _5\mathcal {I}+\rho _3\mathcal {B}*\mathcal {B}^T)^{-1} \end{aligned}$$

(16)

Note that the calculation of inverse tensors in (15) and (16) are not hard, since only the first front slices of $\rho _4\mathcal {I}+\rho _2\mathcal {A}^T*\mathcal {A}$ and $\rho _5\mathcal {I}+\rho _3\mathcal {B}*\mathcal {B}^T$ are non-zero.

Computing $\varvec{\mathcal {X}}$ . The subproblem for $\mathcal {X}$ is

$$\begin{aligned} \begin{aligned} \mathcal {X}^{k+1} = \mathop {\mathrm{arg\,min}}\limits _\mathcal {X}\quad&\frac{\rho _1}{2} \left\| \mathcal {S}^k-\mathcal {X}+\frac{\mathcal {U}^k}{\rho _1}\right\| _F^2 + \frac{\rho _4}{2} \left\| \mathcal {Z}_1^k-\mathcal {X}^k+\frac{\mathcal {W}_1^k}{\rho _4}\right\| _F^2\\&+ \frac{\rho _5}{2} \left\| \mathcal {Z}_2^k-\mathcal {X}^k+\frac{\mathcal {W}_2^k}{\rho _5}\right\| _F^2 \end{aligned} \end{aligned}$$

(17)

So update $\mathcal {X}$ by

(18)

Updating Multipliers

(19)

With these update formulae, we conclude the solver in Algorithm 1.

Fig. 1.

RGB-color images used in our experiment. From left to right they are (a) Airplane (b) Baboon (c) Barbara (d) Facade (e) House (f) Lena (g) Peppers (h) Sailboat

4 Experiments

In this section, we evaluate our methods on eight benchmark RGB-color images with different types of missing entries. The eight benchmark images are showed in Fig. 1. Each image is 256 $\times$ 256 and has 3 color channels, so it is a $256\times 256\times 3$ tensor. We compare our method (t-SVD-TV), with five state-of-art methods: HaLRTC [7], FBCP [19], t-SVD [18], LRTC-TV-I and LRTC-TC-II [6]. Relative Square Error (RSE) and Peak Signal to Noise Ratio (PSNR) are used to assess the recovery result, and if we denote true data as $\mathcal {T}$, RSE and RSNR are defined as

$$\begin{aligned} \text {RSE}&= \frac{\Vert \mathcal {X}-\mathcal {T}\Vert _F}{\Vert \mathcal {T}\Vert _F}\end{aligned}$$

(20)

$$\begin{aligned} \text {PSNR}&= 10\log _{10} \frac{\mathcal {T}_{\max }^2}{\Vert \mathcal {X}-\mathcal {T}\Vert _F^2} \end{aligned}$$

(21)

where $\mathcal {T}_{\max }$ is the maximum value in $\mathcal {T}$. Better recovery result will have a smaller RSE and larger PSNR.

Parameter Settings. The key parameters in our methods are $\lambda _1$ and $\lambda _2$. Since they are balancing the weights of vertical and horizontal gradient, and in general vertical and horizontal gradient are of the same importance, so we set $\lambda _1=\lambda _2$. And by experience, we set $\lambda _1=\lambda _2=0.01$ in our experiments. Other parameters such as $\rho _i (i=1,...,5)$ are concerned with the convergence property of the algorithm, and in our experiments we set $\rho _1=\rho _2=0.001$, $\rho _3=\rho _4=\rho _5=0.1$.

Color Image Inpainting. We first compare our methods with the five state-of-art methods under different missing rates. We use Baboon in Fig. 1 to illustrate the different inpainting performances with random missing entries. As is shown in Fig. 2, our method performs well for both low and high missing rates while others have their limitations. For example, FBCP only performs well when missing rate is high while results of LRTC-TV-I and LRTC-TV-II are not so good with such a high missing rate.

Fig. 2.

Result of recovering Baboon with random missing entries

Then we test our method with the eight images in Fig. 1 with 50% random missing entries. The results is shown in Table 1, from which we can see that our method outperforms others in most pictures and only the result on Peppers is an exception.

Table 1. Result of recovering different images with 50% missing entries

Finally, we present the visual effect of the inpainting algorithms in Fig. 3. The first line is random missing entries with rate 30%. The second line is random missing pixels with rate 30%. The third line is simulated scratches. And we can see that our method performs well in local details while preserving global structures.

Fig. 3.

Comparison of inpainting image Facade. The first line is random missing entries with rate 30%. The second line is random missing pixels with rate 30%. The third line is simulated scratches.

5 Conclusions

In this paper, we aim to take both low-rank and total-variation constraint into consideration to complete visual data with missing entries. We propose a novel tensor named gradient tensor by using the t-product framework, then we fuse the novel tensor framework and classic TV together and we verify the effectiveness of our method by experiments. Our future work will focus on design a tensor framework directly that ensure global low-rank property and local smoothness.