Pore-Scale Facial Features Matching Under 3D Morphable Model Constraint

Abstract

Similar to irises and fingerprints, pore-scale facial features are effective features for distinguishing human identities. Recently, the local feature extraction based on deep network architecture has been proposed, which needs a large dataset for training. However, there are no large databases for pore-scale facial features. Actually, it is hard to set up a large pore-scale facial-feature dataset, because the images from existing high-resolution face databases are uncalibrated and nonsynchronous, and human faces are nonrigid. To solve this problem, we propose a method to establish a large pore-to-pore correspondence dataset. We adopt Pore Scale-Invariant Feature Transform (PSIFT) to extract pore-scale facial features from face images, and use 3D Dense Face Alignment (3DDFA) to obtain a fitted 3D morphable model, which is constrained by matching keypoints. From our experiments, a large pore-to-pore correspondence dataset, including 17,136 classes of matched pore-keypoint pairs, is established.

D. Li—This work was supported by National Natural Science Foundation of China: 61503084, U1501251 and Natural Science Foundation of Guangdong Province, China: 2016A030310348, and RGC General Research Fund, Hong Kong: PolyU 152765/16E.

1 Introduction

Pore-scale facial features include pores, fine wrinkles, and hair, which commonly appear in the whole face region. Pore-scale facial features, which are similar to the features for irises and fingerprints, are one of the most effective features for distinguishing human identities. Recently, local feature extraction based on deep network architecture [1], namely Learned Invariant Feature Transform (LIFT), has been proposed. LIFT is a deep network architecture that implements the full feature-point handling pipeline, i.e. detection, orientation estimation, and feature description. If LIFT is trained with a large and accurate dataset, it can perform better than state-of-the-art methods for feature extraction. This inspires us to believe that good pore-scale feature extraction can be achieved if LIFT is trained under a large pore-scale facial-feature dataset. However, currently, there are no large and open databases of pore-scale facial features. Therefore, in this paper, we first propose an efficient method for generating a large pore-to-pore correspondence dataset.

It is hard to set up a large pore-to-pore correspondence dataset, because the images from existing high-resolution (HR) face databases are uncalibrated and nonsynchronous. Besides, human faces are nonrigid. All these make pore-scale feature matching a great challenge. To the best of our knowledge, only a few studies have been reported in the literature that attempt to set up a pore-to-pore correspondences dataset using uncalibrated face images. Lin et al. [2] employed the SURF features [3] on facial images with viewpoints of about 45${}^{\circ }$-apart, which typically obtained no more than 10 inliers (i.e. correctly matched keypoint pairs) out of a total of 30 matched candidates in 3 poses. Li et al. [4] proposed a new framework, namely Pore Scale-Invariant Feature Transform (PSIFT), to achieve the pore-scale feature extraction, and also generate a pore-to-pore correspondence dataset, including about 4,240 classes of matched pore-keypoint pairs. PSIFT is a feature that can describe the human pore patches distinctively. However, the human face is symmetic, and PSIFT may produce some outliers. For this problem, Li [4] uses the RANSAC (Random SAmple Consensus) [14] method to discard the potential outliers, which will result in reducing the number of matched keypoints. We found that the RANSAC algorithm cannot perform satisfactorily, if the object under consideration is nonrigid. Therefore, Li’s method [4] also removes many matched keypoints from facial regions. In our opinion, one of the most promising ways of establishing a larger pore-to-pore correspondence dataset is finding a new constraint, which can perform well for pore-scale feature matching.

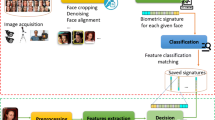
Currently, some research solves the face-alignment problem with a 3D solution. Blanz et al. [11] proposed a standard 3D morphable model (3DMM), and Zhu et al. [10] presented a neural network structure, namely 3D Dense Face Alignment (3DDFA), to fit the 3D morphable model to a face image. Inspired by the 3DDFA algorithm, in this paper we use the fitted 3D morphable model to constrain the pore-scale keypoint matching. To the best of our knowledge, 3D-model constraint is one of the most effective constraints for keypoint matching. Our proposed framework is shown in Fig. 1. In summary, our contributions are:

• 1. We propose the 3D morphable model constraint, which can improve the accuracy for pore-scale keypoint matching.

• 2. Our proposed methods can establish a large number of correspondences between uncalibrated face images of the same person using the pore-scale features, which leads to many potential applications. Our work shows a method to merge face-based approaches with general computer-vision approaches.

• 3. Based on our framework, a pore-to-pore correspondences dataset containing 17,136 classes of matched pore-keypoint pairs, is established, where the same pore keypoints from 4 face images of the same subject, with different poses, are linked up.

Fig. 1.

The structure of the proposed overall framework.

2 Pore-Scale Invariant Feature Transform

PSIFT [4] is variant of SIFT [9], which can generate pore-scale features. The details of PSIFT will be introduced in the following sections.

2.1 Pore-Scale Feature Detection

Pore-scale facial features, such as pores and fine wrinkles, are darker than their surroundings in a skin region. Therefore, PSIFT applies the Difference-of-Gaussians (DoG) detectors for keypoint detection on multiple scales, which is shown as follows.

$$\begin{aligned} D(x,y,\sigma ) = L(x,y,k\sigma )-L(x,y,\sigma )=(G(x,y,k\sigma )-G(x,y,\sigma ))*I(x,y), \end{aligned}$$

(1)

where the scale space of an image $L(x,y,\sigma )$ is the convolution of the image I(x,y) and the Gaussian kernel

$$\begin{aligned} G(x,y,\sigma )=\frac{1}{2\pi \sigma ^2}exp(\frac{-(x^2+y^2)}{2\sigma ^2}). \end{aligned}$$

(2)

PSIFT constructs the DoG in octaves, which have the $\sigma$ doubled in the scale space. Li [4] found that the PSIFT detector only needs the maxima of the DoG to locate the darker pore keypoints in face regions. An example is shown in Fig. 2(c). This is because a blob-shaped pore-scale keypoint is a small, darker point due to its small concavity, where incident light is likely to be blocked. Therefore, PSIFT models the blob-shaped skin pores using a Gaussian function, as follows:

$$\begin{aligned} pore(x,y,\sigma )=1-2\pi \sigma ^2G(x,y,\sigma ), \end{aligned}$$

(3)

where $\sigma$ is the scale of the pore model. Then, the DoG response to a pore, denoted as $D_{pore}$, can be computed as follows:

$$\begin{aligned} D_{pore}(x,y,\sigma _1,\sigma _2)=[G(x,y,k\sigma _1)-G(x,y,\sigma _1)]*pore(x,y,\sigma _2), \end{aligned}$$

(4)

and the pore-scale keypoints are the maxima of $D_{pore}$.

Fig. 2.

(a) Four face images with different skin conditions from the Bosphorus face database, (b) local skin-texture images, and (c) the DoG of the local skin-texture image.

2.2 Pore-Scale Feature Descriptor

The local PSIFT descriptor, which is adapted from SIFT, is used to extract the relative-position information about neighboring pores. The keypoints from two facial-skin regions can be matched by using the PSIFT descriptor. Figure 2 shows some sample results of the DoG layers. The lighter points on a DoG, as shown in Fig. 2(c), represent the responses of the feature points. These points are very similar to each other: most of them are blob-shaped, and the surrounding region of the keypoints have almost the same color. However, the relative positions of the pores are unique. Therefore, the descriptor should extract not only the information around the keypoints, but also the information of a neighborhood wide enough to include the neighboring pore-scale features. Therefore, both the number of subregions and the support size of these subregions for the PSIFT descriptor should be sufficiently large. Besides, Li [4] found that the keypoints are not assigned a main orientation, because most of the keypoints do not have a coherent orientation. Some parameters of the PSIFT and SIFT descriptors are shown in Table 1.

Table 1. The parameters of the PSIFT and SIFT descriptors

3 Matching with the 3D Morphable Model Constraint

In order to achieve a more efficient and accurate matching, we present our method for local PSIFT feature matching by using the 3D-model constraint. The details of our method are introduced in the following sections.

3.1 3D Morphable Model

Blanz et al. [11] proposed the 3D morphable model (3DMM), which describes the 3D face space with principal component analysis (PCA), as follow:

$$\begin{aligned} S = \bar{S} + A_{id}\alpha _id + A_{exp}\alpha _{exp}, \end{aligned}$$

(5)

where S is a 3D face, $\bar{S}$ is the mean shape, $A_{id}$ is the principal axes trained on the 3D face scans with neutral expression, $\alpha _{id}$ is the shape parameter, $A_{exp}$ is the principal axes trained on the offsets between different expression scans, and $\alpha _{exp}$ is the expression parameter. For this, $A_{id}$ and $A_{exp}$ come from Basel Face Model (BFM) [12] and Face-Warehouse [13] respectively. The 3D face is then projected onto the image plane with Weak Perspective Projection, as follows:

$$\begin{aligned} V(p) = f*Pr*R*(\bar{S} + A_{id}\alpha _id + A_{exp}\alpha _{exp}) + t_2d, \end{aligned}$$

(6)

where V(p) is the constructed model and projection function, leading to the 2D positions of the model vertexes; f is the scale factor; Pr is the orthographic projection matrix $Pr = \big ({\begin{matrix}1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \end{matrix}}\big )$; R is the rotation matrix constructed from rotation angles pitch, yaw, and roll; and $t_{2d}$ is the translation vector. The collection of all the model parameters is $p = [f,pitch,yaw,roll,t_{2d},\alpha _{id},\alpha _{exp}]^T$.

3.2 3D Dense Face Alignment

Zhu et al. [10] presented a network structure, namely 3D Dense Face Alignment (3DDFA), to compute the model parameters p. The purpose of 3D face alignment is to estimate p from a single face image $\mathbf I$. 3DDFA [10] employs a unified network structure across the cascade and constructs a specially designed feature Projected Normalized Coordinate Code (PNCC). In summary, at iteration k (k = 0, 1,..., K), given an initial parameter set $p^k$, 3DDFA constructs PNCC with $p^k$, and trains a convolutional neutral network $Net^k$ to predict the parameter update $\varDelta p^k$:

$$\begin{aligned} \varDelta p^k = Net^k(\mathbf I ,PNCC(p^k)). \end{aligned}$$

(7)

After that, a better parameter set $p^{k+1} = p^k+\varDelta p^k$ becomes the input of the next network $Net^{k+1}$, which has the same structure as $Net^k$. The input is a $100 \times 100 \times 3$ color image of PNCC. The network contains four convolution layers, three pooling layers, and two fully connected layers, and the network structure is shown in Fig. 3. The output is a 234-dimensional updated parameter set, including 6-dimensional pose parameters $[f, pitch, yaw, roll, t_{2dx},t_{2dy}]$, 199-dimensional shape parameters $\alpha _{id}$, and 29-dimensional expression parameters $\alpha _{exp}$. The result, based on 3DDFA, after the 3rd iteration is shown in Fig. 4.

Fig. 3.

An overview of 3DDFA.

Fig. 4.

(a) The original image, and (b) the image with 3D-model projection.

3.3 3D Morphable Model Constraint

A pore keypoint is a pore pointin a face image. Therefore, we can write the equations of the probe image and the gallery image from Eq. (6) as follows.

$$\begin{aligned} V_{p}(pore) = f_{p}*Pr*R_{p}*(\bar{S}_{p}(pore) + A_{id}\alpha _{id_{p}} + A_{exp}\alpha _{exp_p}) + t_{2d_p}, \end{aligned}$$

(8)

$$\begin{aligned} V_{g}(pore) = f_{g}*Pr*R_{g}*(\bar{S}_{g}(pore) + A_{id}\alpha _{id_{g}} + A_{exp}\alpha _{exp_g}) + t_{2d_g}, \end{aligned}$$

(9)

where $\bar{S}_{p}(pore)$ and $\bar{S}_{g}(pore)$ are the 3D location of the pores of the mean shape. From Eqs. (8) and (9), we assume that if a pore keypoint of the probe image and a pore keypoint of the gallery image are the same pore keypoint of the face, then $Err_{3d} = ||\bar{S}_{g}(pore) - \bar{S}_{p}(pore)||_{2}$ approximately equals 0. Then, we can compute the following:

$$\begin{aligned} V_{pg}(pore) = f_{g}*Pr*R_{g}*(\bar{S}_{p}(pore) + A_{id}\alpha _{id_{g}} + A_{exp}\alpha _{exp_g}) + t_{2d_g} \end{aligned}$$

(10)

$$\begin{aligned} Err_2d = ||V_{pg}(pore)-V_{g}(pore)||_2 < range, \end{aligned}$$

(11)

where $f_{g}$, $R_{(g)}$, $\bar{S}_p(pore)$, $\alpha _{id_{g}}$, $\alpha _{exp_g}$, and $t_{2d_g}$ can be computed from 3DDFA. This means that if range is set correctly and the same pore patch can be detected in the probe image and the gallery image, Eq. (11) will be true. Then, we only need to compute the nearest neighbor rate of the neighboring feature of $V_{pg}(pore)$. If the rate is less than a threshold, the matched keypoint between the probe and gallery images will be found. The estimation of the keypoint positions matched based on the pore-scale facial features is summarized in Algorithm 1.

Fig. 5.

(a) A face image in the neutral pose, (b) the face at a yaw rotation of 10${}^{\circ }$. The red points in (b) represent the neighboring keypoints of $V_{pg}(pore)$, and the green point in (b) is the matched point of (a).

In our algorithm, we do not use RANSAC [14] to identify those inliers, because the 3D morphable model constraint can identify the inliers accurately, and detect more matched keypoints. Some examples are shown in Fig. 5, where the green point in Fig. 5(a) is one of the pore keypoints, while the red points in Fig. 5(b) are the neighbors of the green point in Fig. 5(a), by using the 3D-model constraint. Besides, the green point in Fig. 5(b) is the matched pore keypoint of the green point in Fig. 5(a).

4 Experiment

In this section, we will evaluate the performances of our proposed method in terms of accuracy for pore matching. The face images used in the experiments are the original size from the Bosphorus database [15].

4.1 Skin Matching Based on the Bosphorus Dataset

In this section, we estimate the performance of each stage of our algorithm for facial skin matching. We use 105 skin-region pairs cropped from 420 face images, which were captured at 10${}^{\circ }$, 20${}^{\circ }$, 30${}^{\circ }$, and 45${}^{\circ }$  to the right of the frontal view in the Bosphorus database, as shown in Figs. 2 and 6. Considering the fact that the dataset is uncalibrated and unsynchronized, Li [4] set the distance threshold used in RANSAC at 0.0005, so only limited number of accurate matching results can be obtained. On the contrary, our method uses 3D-model constraint, so we can obtain more matched keypoints than Li’s method [4]. Table 2 illustrates the numbers of inliers obtained by the two methods. Table 2 shows that our method can detect many more matched keypoints, so our method can be used to generate a larger pore-to-pore correspondence dataset.

Table 2. Skin matching results in terms of number of inliers detected

Fig. 6.

Images of the same subject at different poses. The red points are the keypoints of the skin region, and the green points are the corresponding keypoints at another pose.

4.2 Pore-to-pore Correspondences Dataset

With the improvement achieved by PSIFT with the 3D-model constraint, a larger pore-to-pore correspondences dataset can be constructed, so that the learning for pore-keypoint-pair matching can be conducted. For each subject, its pore keypoints at one pose are matched to the corresponding pore keypoints at an adjacent pose. We have established three sets of matched keypoint pairs, with viewing angles at 10${}^{\circ }$  and 20${}^{\circ }$, 20${}^{\circ }$  and 30${}^{\circ }$, and 30${}^{\circ }$  and 45${}^{\circ }$. After finding a set of matched pore keypoints between each image pair, we use the matched keypoints to form tracks. A track is a set of matched keypoints across the face images of the same subject at different poses. If a track contains more than one keypoint in the same image, it is considered to be inconsistent, and is then removed. We choose only those consistent tracks, containing 4 keypoints corresponding to the 10${}^{\circ }$, 20${}^{\circ }$, 30${}^{\circ }$, and 45${}^{\circ }$ poses, as shown in Fig. 6. Finally, 17,136 tracks are established, which is much larger than the pore-to-pore correspondences dataset established in Li [4]. In addition, we have also generated another larger pore-to-pore correspondences dataset, based on the whole face of the subjects in the Boshorus dataset, which contains 80, 236 tracks.

Fig. 7.

Some patches of a subject: each row consists of the corresponding patches of the same pore keypoints of the face images of the same subject at 10${}^{\circ }$, 20${}^{\circ }$, 30${}^{\circ }$, and 45${}^{\circ }$ poses.

Based on our proposed method, which relies on the PSIFT features, we can match the pore-scale keypoints of the same subject from different perspectives. We extract training patches according to the scale $\sigma$ of the pore keypoints detected. Patches are extracted from a $24\sigma \times 24\sigma$ support region at the keypoint locations, and then normalized to $S\times S$ pixels, where $S = 128$ in our algorithm. Some data from the pore-to-pore dataset is shown in Fig. 7.

5 Conclusion

In this paper, we have proposed using the 3D-model constraint to improve the performance of pore-scale feature matching, which can improve the matching performance when the face images to be matched have a large baseline. Using our proposed method, a larger pore-to-pore correspondences dataset, including 17,136 classes of matched pore-keypoint pairs, is established. In our future work, we will use this larger pore-to-pore correspondences dataset to train a deep neural network so as to learn a better pore-scale feature for face matching. Furthermore, we will evaluate our method under different facial expressions and different light conditions, so that we can produce a pore dataset with different conditions.