Joint Supervision for Discriminative Feature Learning in Convolutional Neural Networks

Abstract

Convolutional Neural Networks have achieved excellent results in various tasks such as face verification and image classification. As a typical loss function in CNNs, the softmax loss is widely used as the supervision signal to train the model for multi-class classification, which can force the learned features to be separable. Unfortunately, these learned features aren’t discriminative enough. In order to efficiently encourage intra-class compactness and inter-class separability of learned features, this paper proposes a H-contrastive loss based on contrastive loss for multi-class classification tasks. Jointly supervised by softmax loss, H-contrastive loss and center loss, we can train a robust CNN to enhance the discriminative power of the deeply learned features from different classes. It is encouraging to see that through our joint supervision, the results achieve the state-of-the-art accuracy on several multi-class classification datasets such as MNIST, CIFAR-10 and CIFAR-100.

1 Introduction

Over the past several years, convolutional neural networks (CNNs) have efficiently boosted the state-of-the-art performance in many fields such as multi-class classification. The pipeline of multi-class classification can be summarized as: feature learning followed by classification. Firstly, the convolutional neural network uses the convolutional layers to learn the features from input images, then the inner-product layer outputs the score $z_{i}=\varvec{w_{i}}\cdot \mathbf {f}$, where f represents the feature learned by the networks, $\varvec{w_{i}}$ represents the weight vector belonging to the class i. Finally the last layer find out the highest score of feature f, which means the input image belongs to the corresponding class. Many advanced network architectures [5,6,7] used softmax loss as the loss function in classification problem, which converges quickly in training and can be easily optimized by SGD (Stochastic Gradient Descent optimizer). If the features are separable in the feature embedding space after training, the tasks can be transformed to simply N classification problem while testing. Thus, it is crucial to learn separable features. Considering the open-set protocol in face verification tasks, where the testing identities are usually disjoint from the training set, the deeply learned features need to be not only separable but discriminative enough. So the deep metric embedding needs to pull similar samples closer and push samples from different classes far away in embedding space. Inspired by the deep metric learning, we want to improve the separability of learned features, narrow the distance between features from the same class, and expand the distance between features from different classes simultaneously in both training and testing phases.

Fig. 1.

Jointly supervised architecture for multi-class classification problem.

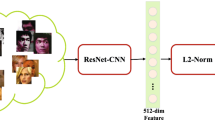
In tasks of classification and face recognition, pioneering works [5,6,7] learned features via the softmax loss, but softmax loss only learned separable features which are not discriminative enough. To improve this, some methods combined softmax loss with contrastive loss [2, 3] or center loss [1] to learn more discriminative features, and [4] adopted triplet loss to supervise the embedding learning, leading to state-of-the-art face recognition results. However, center loss only decreases the intra-class distance while ignoring the inter-class separability. Both contrastive loss and triplet loss require carefully designed pair/triplet mining procedures because the results are sensitive to the mining hard samples, which are time-consuming and the results are determined by the quality of mining procedures. [11] proposed Hard-Aware Deeply Cascaded Embedding based on the contrastive loss to mine hard examples in deep metric embedding. Inspired by [11], we propose the H-contrastive loss function based on the contrastive loss to help efficiently enhance the discriminative power of the learned features in CNNs for classification problem, we will define it in detail in Sect. 3.1. While using the H-contrastive loss, we don’t need to spend any time on the design of hard examples mining procedures. As shown in Fig. 1, the softmax loss learns separable features, the H-contrastive loss produces decision margin between features from different classes, the center loss further decreases the distance between features from the same class. With the joint supervision, not only the inter-class distances are enlarged, but also the intra-class distances are shrunk down.

Our major contributions can be summarized as follows:

• 1. We propose the H-contrastive loss for CNNs to enhance the discriminative power of learned features, which doesn’t need to design pair mining procedures to pick hard samples.

• 2. We show that H-contrastive loss is robust enough and can be jointly supervised with other loss functions in CNNs easily. By using softmax loss, H-contrastive loss and center loss to jointly supervise the training, we achieved the state-of-the-art performance on several multi-class classification datasets, e.g. MNIST, CIFAR-10, and CIFAR-100.

2 Related Work

Center Loss. Wen et al. [1] proposed center loss to simultaneously learn a center for deep features of each class and penalize the distances between the deep features and their corresponding class centers. The softmax loss pushes deep features from different classes away from each other during training, while center loss forces deep features from the same class closer to the center of the class. The main idea of center loss is to shrink down the intra-class distance, then use the softmax loss to jointly supervise the training for expanding inter-class distance. Thus the ability in this joint supervision to force the features from different class is the same as the supervision conducted by softmax loss only. Different from the center loss, H-contrastive loss can accomplish these two tasks itself.

Large-Margin Softmax Loss. Liu et al. [9] proposed a loss function based on the softmax loss, called Large-Margin Softmax Loss(L-Softmax), to concentrate more on the angular decision margin between different classes by defining an adjustable margin parameter m. L-Softmax loss can replace the softmax loss in the training of CNNs, it firstly constrains L$_2$-normalization on both features f and weight vector $\varvec{w_i}$, then enlarges the decision margin between different classes based on the cosine similarity.

Contrastive Loss/Triplet Loss. Because of the high intra-class and low inter-class variance, metric learning with CNNs [2,3,4] use contrastive loss and triplet loss to construct loss functions for image pairs and triplets. The goal is to use a CNN to learn a feature embedding that captures the semantic similarity among images. Unlike deep learning, deep metric learning usually takes pairs or triplets of samples as input, and outputs the distance between them. The most widely used metric learning methods are contrastive loss and triplet loss, both of the two loss functions optimize the normalized Euclidean distance between feature pairs/triplets. But it is almost impossible to deal with all possible combinations during training, so sampling and mining procedures are necessary [4], and usually, these procedures are time-consuming. On the contrary, H-contrastive loss can jointly supervise the CNN training with other loss functions and be optimized by SGD easily without procedure carefully designed to mine hard examples.

3 The Proposed H-Contrastive Loss Function

In this section, we elaborate our approach, and use some toy examples to intuitively show the distributions of deeply learned features supervised by different loss functions.

3.1 Definition

First we give the notations that will be used to describe our method:

• P = {I$_i^+$, I$_j^+$}: all the positive input image pairs constructed from the mini-batch training set, where I$_i^+$ and I$_j^+$ are supposed to belong to the same class.

• N = {I$_i^-$, I$_j^-$}: all the negative input image pairs constructed from the mini-batch training set, where I$_i^-$ and I$_j^-$ are supposed to come from different classes.

• {f$_i^+$, f$_j^+$}: the computed feature vector for positive pairs {I$_i^+$, I$_j^+$} after the transform function that transform the output of the computation block to a low dimensional feature vector for distance calculation.

• {f$_i^-$, f$_j^-$}: the computed feature vector for negative pairs {I$_i^-$, I$_j^-$}.

The H-contrastive loss is defined as:

$$\begin{aligned} L_{H} = \sum _{\left( i,j\right) \in P}L^+(i,j) + \sum _{\left( i,j\right) \in N}L^-(i,j) \end{aligned}$$

(1)

$$\begin{aligned} L^{+}(i,j) = D(f_{i,h}^{+},f_{j,h}^{+}) \end{aligned}$$

(2)

$$\begin{aligned} L^-(i,j) = max\,\{0,\,M - D(f_{i,h}^-,f_{j,h}^-)\} \end{aligned}$$

(3)

where D(f $_{i,h}$, f $_{j,h}$) is the Euclidean distance between the two L$_2$-normalized feature vectors f $_{i,h}$ and f $_{j,h}$, M is the margin. It is difficult to predefine thresholds for hard sample selection as the loss distributions keep changing during training, so we use a simple way by ranking distances of all positive pairs in a mini-batch, and take top h percent samples as hard positive set, and similarly for hard negative example mining. In this way, we don’t need to design the mining procedure and can still pick out hard samples. We use a hyperparameter h to control hard ratio in training, (f $_{i,h}$, f $_{j,h}$) means top h percent feature pairs in (f $_i$, f $_j$).

The original softmax loss and center loss can be written as:

$$\begin{aligned} L_S = -\frac{1}{m}\sum _{i=1}^m \log \frac{e^{W^T_{y_i}f_i+b_{y_i}}}{\sum _{j=1}^n e^{W^T_jf_i+b_j}} \end{aligned}$$

(4)

$$\begin{aligned} L_C = \sum _{i=1}^m {\Vert x_i - c_{y_i} \Vert }_2^2 \end{aligned}$$

(5)

In Eq. (4), m is the batch size in training, n is the number of classes, x $_i$ denotes the ith deep feature, y $_i$ is the corresponding class label, W and b are weight and bias for the inner-product layer of CNNs. The $c_{y_i}$ in Eq. (5) denotes the y $_i$th class center of learned features. We adopt the joint supervision of softmax loss, H-contrastive loss and center loss to train the CNNs to learn more discriminative features, the formulation is given in Eq. (6). $\lambda _1$ and $\lambda _2$ are used for balancing the three loss functions.

$$\begin{aligned} L = L_S + \lambda _1L_H + \lambda _2L_C \end{aligned}$$

(6)

Table 1. The CNN architectures for MNIST/CIFAR-10/CIFAR-100. Conv1.x denotes convolution units that may contain multiple convolution layers. E.g., [5 $\times$ 5, 32] $\times$ 2 denotes 2 cascaded convolution layers with 32 filters of size 5 $\times$ 5. All the pooling layers have the same pooling strides of 2.

Fig. 2.

2-D feature distribution on MNIST dataset’s test set. (a) Features learned in CNN supervised by softmax loss only. (b) Features learned in CNN jointly supervised by softmax loss and H-contrastive loss, it is obviously to see the distance between different classes is larger than (a). (c) Features learned in CNN jointly supervised by softmax loss and center loss, features from the same class are closer to their center. (d) Features learned in CNN jointly supervised by softmax loss, center loss and H-contrastive loss, H-contrastive loss helps to not only further expand the distance between different classes and narrow the intra-class distance, but also decrease the features scattered in the middle.

3.2 Toy Examples

In order to give an intuitive feeling about the distribution of deeply leaned features, we did some toy examples based on Wen et al.’s model in [1] except for some minor modifications on the MNIST [8] dataset, the CNN architecture we adopt is shown in Table 1. We reduce the output number of the fully connected (FC) layer to 2, which means the dimension of the deep features is 2, and then plot them by class, as shown in Fig. 2. We decrease the output number of the FC layer which affects the performance, that is the reason why the testing accuracy is not as good as Table. 2. We can find that under the supervision of softmax loss, the deeply learned features are separable, but not discriminative enough. Through the joint supervision, our H-contrastive loss enhances the discriminative power of features significantly.

3.3 Discussion

If we only use softmax loss to supervise the CNN, the features in test set would have short inter-class distances as well as long intra-class distances. After the joint supervision with center loss, features would have shorter intra-class distances, but the angle between different classes has no change, in other word, the cosine similarity between two different classes is the same as the features supervised by softmax loss only. The H-contrastive loss can help decrease the intra-class distance and enlarge angle between different classes efficiently.

4 Experiments

4.1 Experimental Settings

We evaluate the loss functions in three standard benchmark datasets: MNIST [8], CIFAR-10 [21] and CIFAR-100 [21]. In testing stage, we only use the softmax loss to classify the samples in all datasets. For convenience, we use HC to denote the H-contrastive loss, and the training on the same dataset supervised by different loss functions use the same CNN shown in Table 1.

General Settings: Our general framework to train and extract deeply learned features is illustrated in Fig. 1, while using softmax loss, center loss and H-contrastive loss to jointly supervise the training, we fix the $\lambda _1$ to 1 and the $\lambda _2$ to 0.05, the different combinations of $\lambda _1$ and $\lambda _2$ are analysed in Sect. 4.4 in detail, and set the margin M in H-contrastive loss function to 0.4. We implement the CNNs using the Caffe library [12] with our modifications. For experiments, we adopt the ReLU [10] as the activation function, a weight decay of 0.0005 and momentum of 0.9, and the batch size for all experiments is 256, in all convolution layers, the stride is set to 1. The weight initialization in [13] and batch normalization [14] are used in our networks to replace the dropout. For optimization, the SGD will work well, and during the training and testing, we don’t adopt any data augmentation setup.

MNIST/CIFAR-10/CIFAR-100: We start with a learning rate of 0.1, divide it by 10 when the error plateaus, finally terminate training at 10k/30k/30k iterations in corresponding datasets. The training data and testing data is 60k/10k, 50k/10k and 50k/10k split following the standard settings for MNIST, CIFAR-10 and CIFAR-100.

4.2 Multi-class Classification Results

MNIST: The network architecture we adopt is shown in Table 1. It is obvious that our method boosts the performance efficiently, improves the softmax from 0.35% to 0.29%, improves the L-Softmax from 0.30% to 0.27% and improves the result supervised by softmax and center loss from 0.31% to 0.25%. Moreover, we use the same architecture with [9], and through joint supervision our method can achieve the sate-of-the-art results while training with less iterations on MNIST, and we believe that the improvement in relative error rate is more worthy of attention.

Table 2. Error rate (%) on MNIST/CIFAR-10/CIFAR-100.

CIFAR-10: Table 1 also shows the CNN architecture that we use to evaluate our method. Firstly, we reproduce the results following the same setting in [9], the L-Softmax has effectively improved the softmax loss and the performance of L-Softmax is already very high. The second column in Table 2 quantifies the effectiveness of our H-contrastive loss. Our H-contrastive loss improved the softmax loss from 8.59% to 7.38%, improved the L-Softmax loss from 7.60% to 7.09%, which is illustrated in Fig. 3(a). We achieve the best performance by jointly supervising the CNN with softmax loss, center loss and H-contrastive loss, which improve the error rate from 7.24% to 6.89%.

CIFAR-100: We also evaluate our method on more complicated dataset CIFAR-100 which has 10000 testing images belonging to 100 classes to further verify the effectiveness of H-contrastive loss and the necessity of joint supervision. The results are shown in the third column in Table 2, and are also illustrated in Fig. 3(b), the CNN architecture refers to Table 1. One can notice that the joint supervision outperforms the CNN with the other competitive methods. H-contrastive loss improved the softmax loss from 31.80% to 30.24%, improved the L-Softmax loss from 29.53% to 29.17% and beat the CNN jointly supervised by softmax loss and center loss for decreasing the error rate from 26.59% to 25.80%. We use the joint supervision to promote the performance for 6.00%, improving the performance from original 31.80% to 25.80%, and get the state-of-the-art result on the CIFAR-100.

Fig. 3.

Error rate vs. iteration with different loss functions on (a) CIFAR-10. (b) CIFAR-100.

Fig. 4.

Error rate vs. iteration with different hard ratios h on (a) CIFAR-10. (b) CIFAR-100.

4.3 Experiments on Parameter h

We also conduct experiments on CIFAR-10 and CIFAR-100 to investigate how the hard ratio h influences the result. Table 3 shows that different h lead to different results and we can see consistent improvement for all different choices of the h, in which S means softmax loss, C means center loss and HC means H-contrastive loss. With proper h, the performance of our method can be significantly boosted, which are illustrated in Fig. 4.

Table 3. Error rate (%) on CIFAR-10 and CIFAR-100 with different h.

4.4 Experiments on Parameters $\lambda _1$ and $\lambda _2$

The hyperparameters $\lambda _1$ and $\lambda _2$ determine the inter-class separability and the intra-class variations in the joint supervision. Both of them are essential for the training, so we conduct two experiments to investigate the results in terms of various combination weights.

In the first experiment, we fix $\lambda _1$ to 0.5, vary $\lambda _2$ from 0.0001 to 1 to supervise the training, the accuracies of the joint training on CIFAR-10 dataset are shown in Fig. 5(a). But the vanishing gradient problem occurs during the training when $\lambda _2$ is higher than 0.1, we think it is mainly caused by the initialization’s instability of the center loss. Except that, it is very clear that using other loss functions to jointly train the CNN can obviously improve the results. In the second experiment, we fix $\lambda _2$ to 0.05 and vary $\lambda _1$ from 0.0001 to 1 to supervise the training, as shown in Fig. 5(b). Properly choosing the combination weights of $\lambda _1$ and $\lambda _2$ can train the network to learn more discriminative features and improve the accuracy on the multi-class classification dataset.

Fig. 5.

Accuracies on CIFAR-10 dataset, which were respectively achieved by the same network settings except the values of hyperparameters $\lambda _1$ and $\lambda _2$. (a) results with different $\lambda _2$ while fixed $\lambda _1$ = 0.5, (b) results with different $\lambda _1$ while fixed $\lambda _2$ = 0.05.

5 Conclusion

In this paper, we propose H-contrastive loss based on the contrastive loss to help increase the inter-class separability and decrease the intra-class distance at the same time. We recommend that center loss and H-contrastive loss should jointly supervise the training. Extensive experiments on MNIST, CIFAR-10 and CIFAR-100 verify the effectiveness of our method and show clear advantages over current state-of-the-art CNNs and all compared baselines. In the future, we are going to evaluate our method on larger dataset like ImageNet and on other field such as face verification tasks.