Abstract
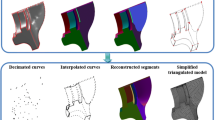
The surface curvature of the polygonal model represents a local shape feature of polygonal surface around one surface point. It has been used to analyze the shape of mesh model. In this paper, we present a novel approximation method of multi-scale surface curvature based on mesh simplification, which computes the Gaussian-weighted average of the mean curvature in different sized neighbor regions at a point while changing the resolution of the polygonal mesh. The proposed method was tested on different polygonal models and the experimental results showed that the overall shape features of the polygonal models were represented more clearly by our method.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsReferences
Kazmi, I.K., You, L., Zhang, J.J.: A survey of 2D and 3D shape descriptors. In: 10th International Conference on Computer Graphics, Imaging and Visualization, pp. 1–10 (2013)
Zhang, L., Fonseca, M.J., Ferreira, A.: Survey on 3D shape descriptors, Technical Report, DecorAR (FCT POSC/EIA/59938/2004), Fundação para a Cincia e a Tecnologia, Lisboa, Portugal (2007)
Botsch, M., Kobbelt, L., Pauly, M., Alliez, P., Levy, B.: Polygon Mesh Processing. A K Peters Ltd., Natick (2010)
Wikipedia. https://en.wikipedia.org/wiki/Differential_geometry_of_surfaces#Shape_operator
Lee, C.H., Varshney, A., Jacobs, D.W.: Mesh saliency. ACM Trans. Graph. 24, 659–666 (2005)
Wu, J., Shen, X., Zhu, W.: Mesh saliency with global rarity. Graph. Models 75, 255–264 (2013)
Taubin, G.: Estimating the tensor of curvature of a surface from a polyhedral approximation. In: IEEE International Conference on Computer Vision, pp. 902–907 (1995)
Liu, Y., Wang, Y., Lin, Y., Li, L., Qi, C.: Half edge collapse mesh simplification algorithm based on constrained quadric error metric method (MECMSA-CQEM) for model simplification. In: 5th International Conference on Intelligent Networks and Intelligent Systems, pp. 1–4 (2012)
Yirci, M.: A comparative study on polygonal mesh simplification algorithms. Thesis of the Graduate School of Natural and Applied Sciences of Middle East Technical University (2008)
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2017R1D1A1B03035718).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Lee, J., Kim, KA., Choi, YJ. (2018). Multi-scale Surface Curvature Based on Mesh Simplification. In: Park, J., Loia, V., Yi, G., Sung, Y. (eds) Advances in Computer Science and Ubiquitous Computing. CUTE CSA 2017 2017. Lecture Notes in Electrical Engineering, vol 474. Springer, Singapore. https://doi.org/10.1007/978-981-10-7605-3_172
Download citation
DOI: https://doi.org/10.1007/978-981-10-7605-3_172
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-7604-6
Online ISBN: 978-981-10-7605-3
eBook Packages: EngineeringEngineering (R0)