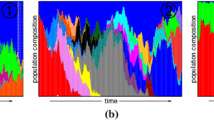
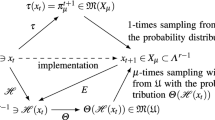
Abstract
Inspired by the successful description of the first steps of molecular evolution by the quasispecies theory and the successful application of quasispecies-like algorithms to optimization problems, we propose a hierarchically organized algorithm. This new algorithm is able to solve a spin glass and a travelling salesman problem using only point mutations. Furthermore, it performs better under comparable circumstances than the ordinary quasispecies algorithm. Depending on the structure of the fitness landscape of the examined problem under consideration the hierarchically organized algorithm proves to be much more suitable than a simple quasispecies algorithm, especially in clustered landscapes. Tuning the error rates reveals the critical minimum copy fidelity necessary to guarantee optimization. We propose to incorporate hierarchical concepts into optimization algorithms inspired by biological evolution, such as genetic algorithms.
Similar content being viewed by others
References
Ambati BK, Ambati J. Mokhatar MM (1991) Heuristic combinatorial optimization by simulated darwinian evolution: a polynomial time algorithm for the travelling salesman. Biol Cybern 65:31–35
Bauer G (1990) Biochemische Verwirklichung und Analyse von kontrollierten Evolutionsexperimenten mit RNA-Quasispezies in vitro. Dissertation, University of Braunschweig
Beveridge GSG, Schlechter RS (1970) Optimization theory and practise. McGraw-Hill Kogakusha, Tokyo
Biebricher CK, Eigen M, Gardiner Jr WC (1983) Kinetics of RNA replication. Biochemistry 22:2544–2559
Biebricher CK, Eigen M, Gardiner Jr WC (1984) Kinetics of RNA replication: plus-minus asymmetry and double strand formation. Biochemistry 23:3186–3194
Biebricher CK, Eigen M, Gardiner Jr WC (1985) Kinetics of RNA replication: competition and selection among self-replicating RNA species. Biochemistry 24:6550–6560
Bremermann HJ, Rogson M, Salaf S (1966) Global properties of evolution processes. In: Patecc HH, Edelsack EA, Fein L, Callahan AB (eds) Natural automata and useful simulations. Spartan Books, Washington, pp 3–41
Eiben AE, Aarts EHL, van Hee KM (1989) A general theory of genetic algorithms. Eindhoven University of Technology, computing science notes
Eigen M (1971) Self-organization of matter and the evolution of biological macromolecules. Naturwissenschaften 58:1748–1766
Eigen M (1985) Macromolecular evolution dynamical ordering in sequence space. Ber Bunsenges Phys Chem 89:658–667
Eigen M (1986) The physics of molecular evolution. Chem Scripta 26B:13–26
Eigen M, Schuster P (1979) The hypercycle a principle of natural self-organization. Springer Berlin Heidelberg New York
Eigen M, Schuster P, McCaskill J (1988) Molecular quasi-species. J Phys Chem 92:6881–6891
Eigen M, Schuster P, McCaskill J (1989) The molecular quasispecies. Adv Chem Phys 75:149–263
Fogel DB (1988) An evolutionary approach to the travelling salesman problem. Biol Cybern 60:139–144
Fontana W, Schnabl W, Schuster P (1989) Physical aspects of evolutionary optimization and adaptation. Phys Rev A 40:3301–3321
Fontana W, Griesmacher T, Schnabl W, Stadler PF (1991) Statistics of landscapes based on free energies, replication and degradation rate constants of RNA secondary structure. Monatsh Chem 122:795–819
Galar R (1985) Handicapped individua in evolutionary processes. Biol Cybern 51:1–9
Galar R (1991) Simulation of local evolutionary dynamics of small populations. Biol Cybern 65:37–45
Goldberg DE (1989) Genetic algorithms. Addison-Wesley, Reading, Mass
Grefenstette JJ, Gopal R, Rosmaita B, Van Gucht D (1985) Genetic algorithms for the travelling salesman problem. In: Grefenstette JJ (ed) Proceedings of an international conference on genetic algorithms and their applications, Carnegie-Mellon University, pp 160–168
Grötschel M (1984) Polyedrische Kombinatorik und Schnittebenenverfahren. Preprint no. 38, University of Augsburg
Hamming RW (1986) Coding and information theory, 2nd edn. Prentice Hall, Englewood Cliffs
Holland OA (1987) Schnittebenenverfahren für Travelling-Salesman und verwandte probleme. Dissertation, University of Bonn
Holland JH (1975) Adaption in natural and artificial systems. University of Michigan Press, Ann Arbor
Kirkpatrick S (1977) Frustration and ground state in spin glasses. Phys Rev B 16:4630–4641
Kirkpatrick S, Gelatt CD, Vecchi M (1983) Optimization by simulated annealing. Science 220:671–680
Lawler EL, Lenstra JK, Rinooy Kan AHG, Shmoys DB (eds) (1985) The travelling salesman problem. Wiley, Chichester
Lin S, Kernighan BW (1973) An effective heuristic algorithm for the travelling-salesman problem. Operation Res 21:498–421
McCaskill J (1984) A stochastic theory of macromolecular evolution. Biol Cybern 50:63–73
Nowak M, Schuster P (1989) Error thresholds of replication in finite populations: mutation frequencies and the onset of Muller's ratchet. J Theor Biol 137:375–395
Rechenberg I (1973) Evolutionsstrategie. frommann-holzboog, Stuttgart
Rokhsar DS, Anderson PW, Stein DL (1986) Self-organization in prebiological systems: simulations of a model for the origin of genetic information. J Mol Evol 23:119–126
Sankoff D, Kruskal JP (eds) (1983) Time warps, string edits and macro molecules: the theory and practise of sequence comparison. Addison-Wesley, Reading, Mass
Schuster P, Sigmund K (1985) Dynamics of evolutionary optimization. Ber Bunsenges Phys Chem 89:668–682
Schwefel HP (1968) Experimentelle Optimierung einer Zweiphasendüse. Bericht 35 zum MHD-Staustrahlrohr, AEG Research Institute, Berlin
Schwefel HP (1981) Numerical optimization of computer models. Wiley, Chichester
Sherrington D, Kirkpatrick S (1975) Solvable model of a spin glass. Phys Rev Lett 35:1792–1796
Sorkin GB (1988) Combinatorial optimization, simulated annealing and fractals. IBM Res Rep RC13674 (no. 601253)
Spiegelman S (1970) The Harvey lectures, series 64. Academic Press, New York
Stadler PF, Schnabl W (1992) The landscape of the travelling salesman problem Phys Lett A 161:337–344
Strunk G (1992) Automatisierte Evolutionsexperimente in vitro und natürliche Selektion unter kontrollierten Bedingungen mit Hilfe der Serial Transfer Technik Dissertation, University of Braunschweig
Ulder NLJ, Aarts EHL, Bandelt HJ, van Laarhoven PJM, Pesch E (1991) Genetic local search algorithms for the travelling salesman problem. In: Schwefel HP, Männer R (eds) Parallel problem solving from nature. (Lecture notes in computer science, vol 496) Springer, Berlin Heidelberg New York
Wang Q (1987) Optimization by simulating molecular evolution. Biol Cybern 57:95–101
Weinberger ED (1990) Correlated and uncorrelated fitness landscapes and how to tell the difference. Biol Cybern 63:325–336
Weinberger ED, Stadler PF (1993) Why some fitness landscapes are fractal. J Theor Biol (in press)
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Schober, A., Thuerk, M. & Eigen, M. Optimization by hierarchical mutant production. Biol. Cybern. 69, 493–501 (1993). https://doi.org/10.1007/BF01185421
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF01185421