Abstract
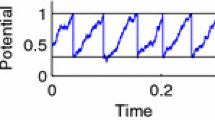
A two-dimensional neuronal model, in which the membrane potential of the dendrite evolves independently from that at the trigger zone of the axon, is proposed and studied. In classical one-dimensional neuronal models the dendritic and axonal potentials cannot be distinguished, and thus they are reset to resting level after firing of an action potential, whereas in the present model the dendritic potential is not reset. The trigger zone is modelled by a simplified leaky integrator (RC circuit) and the dendritic compartment can be described by any of the classical one-dimensional neuronal models. The new model simulates observed features of the firing dynamics which are not displayed by classical models, namely positive correlation between interspike intervals and endogenous bursting. It gives a more natural account of features already accounted for in previous models, such as the absence of an upper limit for the coefficient of variation of intervals (i.e. irregular firing). It allows the first- and second-order neurons of the olfactory system to be described with the same basic assumptions, which was not the case in one-point models. Nevertheless it keeps the main qualitative properties found previously, such as the existence of three regimens of firing with increasing stimulus concentration and the sigmoid shape of the firing frequency of firstorder neurons as a function of the logarithm of stimulus concentration.
Similar content being viewed by others
References
Barbi M, Ferdeghini EM (1980) Relevance of the single ommatidium performance in determining the oscillatory response of the Limulus retina. Biol Cybern 39:45–51
Budelli RW, Soto E, González-Estrada MT, Macadar O (1986) A spike generator mechanism model simulates utricular afferents response to sinusoidal vibrations. Biol Cybern 54:237–244
Correia MJ, Landolt JP (1977) A point process analysis of the spontaneous activity of anterior semicircular canal units in the anesthetized pigeon. Biol Cybern 27:199–213
Davis H (1961) Some principles of sensory receptor action. Physiol Rev 41:391–416
De Kwaadsteniet JW (1982) Statistical analysis and stochastic modeling of neuronal spike train activity. Math Biosci 60:17–71
Døving K, Hyvärinen J (1969) Afferent and efferent influences on the activity pattern of single olfactory neurons. Acta Physiol Scand 75:111–123
Eccles JC (1957) The physiology of nerve cells. Johns Hopkins University Press, Baltimore
Feller W (1968) An introduction to probability theory and its application, vol 1. Wiley, New York
Feller W (1971) An introduction to probability theory and its application, vol 2. Wiley, New York
Floyd K, Hick VE, Holden AV, Koley J, Morrison JFB (1982) Non-Markov negative correlation between interspike intervals in mammalian afferent discharge. Biol Cybern 45:89–93
Galifret Y (1978) Les mécanismes de transduction sensorielle. J Physiol (Paris) 74:121–129
Gerstein GL, Mandelbrot B (1964) Random walk models for the spike activity of a single neuron. Biophys J 4:41–68
Grüneis F, Nakao M, Yamamoto M, Musha T, Nakahama H (1989) An interpretation of 1/f fluctuation in neuronal spike trains during dream sleep. Biol Cybern 60:161–169
Hanson FB, Tuckwell HC (1983) Diffusion approximation for neuronal activity including synaptic reversal potentials. J Theor Neurobiol 2:127–153
Kallianpur G, Wolpert RL (1987) Weak convergence of stochastic neuronal models. In: Kimura M, Kallianpur G, Hida T (eds) Stochastic methods in biology. Springer, Berlin Heidelberg New York, pp 116–145
Keilson J, Ross HF (1975) Passage time distributions for Gaussian Markov (Ornstein-Uhlenbeck) statistical processes. Selected Tables Math Stat 3:233–327
Knight BW (1972) Dynamics of encoding in a population of neurons. J Gen Physiol 59:734–766
Kohn AF (1989) Dendritic transformations on random synaptic inputs as measured from a neuron's spike train. Modeling and simulation. IEEE Trans Biomed Eng 36:44–54
Kuffler SW, Nicholls KR, Martin AR (1984) From neuron to brain. Sinauer, Sunderland, USA
Lánský P (1984) On approximations of Stein's neuronal model. J Theor Biol 107:631–647
Lánský P, Musila M (1991) Variable initial depolarization in Stein's neuronal model with synaptic reversal potentials. Biol Cybern 64:285–291
Lánský P, Radil T (1987) Statistical inference on spontaneous neuronal discharge patterns. Biol Cybern 55:299–311
Lánský P, Rospars JP (1993) Coding of odor intensity. BioSystems (in press)
Lánský P, Smith CE (1989) The effect of a random initial condition in neural first-passage-time models. Math Biosci 93:191–215
Lapicque L (1907) Recherches quantitatives sur l'excitation électrique des nerfs traitée comme une polarisation. J Physiol Pathol Gen 9:620–635
Levine MW (1991) The distribution of the intervals between neural impulses in the maintained discharges of retinal ganglion cells. Biol Cybern 65:459–467
Levine MW, Shefner JM (1977) A model for the variability of interspike intervals during sustained firing of retinal neurons. Biophys J 19:241–252
Nagai T, Ueda K (1981) Stochastic properties of gustatory impulse discharges in rat chorda tympani fibers. J Neurophysiol 45:574–592
O'Neill WD, Lin JC, Ma Y-C (1986) Estimation and verification of a stochastic neuron model. IEEE Trans Biomed Eng 33:654–666
Perkel DH, Mulloney B (1974) Motor pattern production in reciprocally inhibitory neurons exhibiting postinhibitory rebound. Science 185:181–183
Ricciardi LM, Sacerdote L (1979) The Ornstein-Uhlenbeck process as a model of neuronal activity. Biol Cybern 35:1–9
Ricciardi LM, Sato S (1990) Diffusion processes and first-passage-time problems. In: Ricciardi LM (ed) Lectures in applied mathematics and informatics. Manchester University Press, Manchester, pp 206–285
Scharstein H (1979) Input-output relationship of the leaky-integrator neuron model. J Math Biol 8:403–420
Sclabassi RJ (1976) Neuronal models, spike trains and the inverse problem. Math Biosci 32:203–219
Shepherd GM (1988) Neurobiology. Oxford University Press, New York
Smith CE (1979) A comment on a retinal neuron model. Biophys J 25:385–386
Stein RB (1965) A theoretical analysis of neuronal variability. Biophys J 5:173–195
Stein RB, Leung KV, Mangeron D, Oguztöreli (1974) Improved neuronal models for studying neural networks. Kybernetik 15:1–9
Stevens CF (1964) Letter to the editor. Biophys J 4:417–419
Tuckwell HC (1987) Diffusion approximations to channel noise. J Theor Biol 127:427–438
Tuckwell HC (1988) Introduction to theoretical neurobiology. Cambridge University Press, Cambridge, UK
Tuckwell HC, Wan FYM, Wong YS (1984) The interspike interval of a cable model neuron with white noise input. Biol Cybern 49:155–167
Yamamoto M, Nakahama H (1983) Stochastic properties of spontaneous unit discharges in somatosensory cortex and mesencephalic reticular formation during sleep-waking states. J Neurophysiol 49:1182–1198
Yamamoto M, Nakahama H, Shima K, Kodama T, Mushiake H (1986) Markov-dependency and spectral analysis on spike-counts in mesencephalic reticular neurons during sleep and attentive states. Brain Res 366:279–298
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Rospars, J.P., Lánský, P. Stochastic model neuron without resetting of dendritic potential: application to the olfactory system. Biol. Cybern. 69, 283–294 (1993). https://doi.org/10.1007/BF00203125
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00203125