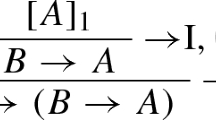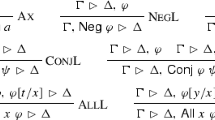Skip to main content
Springer Nature Link
Log in

Goto statements: semantics and deduction systems

  • Published:
Acta Informatica Aims and scope Submit manuscript

Summary

A simple language containing goto statements is presented, together with a denotational and operational semantic for it. Equivalence of these semantical descriptions is proven.

Furthermore, soundness and completeness of a Hoare-like proof system for the language is shown. This is done in two steps. Firstly, a proof system is given and validity is defined using (a variant of) direct semantics. In this case soundness and completeness proofs are relatively easy. After that, a proof system is given which is more in the style of the one by Clint and Hoare [8], and validity in this system is defined using continuation semantics. This validity definition is then related to validity in the first system and, using this correspondence, soundness and completeness for the second system is proven.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Apt, K.R.: A sound and complete Hoare-like system for a fragment of PASCAL. Report IW 97/78 (preprint), Mathematical Centre, Amsterdam, 1978

    Google Scholar 

  2. Apt, K.R., de Bakker, J.W.: Semantics and proof theory of PASCAL procedures. In: Proceedings of the 4th colloquium on automata, languages and programming. Lecture Notes in Computer Science Vol. 52, pp. 30–44, Berlin Heidelberg New York: Springer 1977

    Google Scholar 

  3. Arbib, M.A., Alagić, S.: Proof rules for gotos. Acta Informat. 11, 139–148 (1979)

    Google Scholar 

  4. Back, R.J.R.: Exception handling with multi-exit statements. In: Programmiersprachen und Programmentwicklungen, (H.-J. Hoffmann, Hrsg.). Informatik-Fachberichte Nr. 25, Berlin Heidelberg New York: Springer 1980

    Google Scholar 

  5. Bakker, J.W. de: Mathematical theory of program correctness. London: Prentice Hall 1980

    Google Scholar 

  6. Bakker, J.W. de: Correctness proofs for assignment statements. Report IW 55/76, Mathematical Centre, Amsterdam 1976

    Google Scholar 

  7. Bjørner, D.: Experiments in block-structured goto language modelling: exits versus continuations. In: Winter school on formal specification methods. Lecture Notes in Computer Science Vol. 86 (D. Bjørner, Ed.), Berlin Heidelberg New York: Springer 1980

    Google Scholar 

  8. Clint, M., Hoare, C.A.R.: Program proving: jumps and functions. Acta Informat. 1, 214–224 (1972)

    Google Scholar 

  9. Cook, S.A.: Soundness and completeness of an axiom system for program verification. SIAM J. Comput. 7, 70–90 (1978)

    Google Scholar 

  10. Hoare, C.A.R.: An axiomatic basis for computer programming. Comm. ACM 12, 576–580, 583 (1969)

    Google Scholar 

  11. Jones, C.B.: Denotational semantics of goto: an exit formulation and its relation to continuations. In: The Vienna Development Method: the Meta-Language. Lecture Notes in Computer Science Vol. 61 (D. Bjørner, C.B. Jones, eds.) Berlin Heidelberg New York: Springer

  12. Kieburtz, R.B., Cherniavsky, J.C.: Axioms for structural induction on programs containing block exits. In: Proceedings of the Symposium on Computer Software Engineering, Polytechnic Institute of New York, 1976

  13. Milne, R., Strachey, C: A theory of programming language semantics. London: Chapman and Hall, New York: Wiley (2 Vols) 1976

    Google Scholar 

  14. Nassi, I.R., Akkoyunlu, E.A.: Semantics of repeat break control structure. In: Proceedings of the 8th Princeton Conference on Information Sciences and Systems, pp. 316–321, Princeton University, Dept. of Electrical Engineering New York, 1974

    Google Scholar 

  15. Scott, D., Strachey, C.: Towards a mathematical semantics for computer languages. Proc. Symp. on computers and automata, Polytechnic Institute of Brooklyn, pp. 19–46 (1971); also: Techn. Mon. PRG-6, Oxford Univ. Computing Lab.

  16. Stoy, J.E.: Denotational semantics — the Scott-Strachey approach to programming language theory. Cambridge, Mass: M.I.T. Press 1977

    Google Scholar 

  17. Strachey, C., Wadsworth, C.: Continuations, a mathematical semantics for handling full jumps. Tech. Mon. PRG-11, Oxford Univ. Computing Lab., Programming research group (1974)

  18. Wand, M.: A new incompleteness result for Hoare's system. J. Assoc. Comput. Mach. 25, 168–175 (1978)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematical Centre, Kruislaan 413, 1098, SJ Amsterdam, The Netherlands

    Arie de Bruin

Authors
  1. Arie de Bruin
    View author publications

    You can also search for this author inPubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

de Bruin, A. Goto statements: semantics and deduction systems. Acta Informatica 15, 385–424 (1981). https://doi.org/10.1007/BF00264536

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00264536

Keywords