Koinzidenzfilter mit kurzen Impulsen

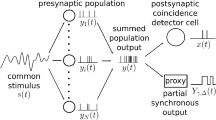
Summary

Coincidence filters consist of one or more threshold elements (e.g. neurons or monostable multivibrators, extended by multiple input gates). They permit the propagation of an impulse train applied to the input only if its repetition rate does not exceed an upper and a lower boundary value. The difference between the upper and the lower boundary value may be defined as the functional bandwidth of the coincidence filter. The functional bandwidth is one of the most interesting characteristic figures of a coincidence filter. By means of this definition, the coincidence filter may be described as a device selecting quickly those impulse trains the repetition rates of which lie within the functional bandwidth

The functional bandwidth depends on the parameters of the impulse trains and of the coincidence filter. This gives rise to the question, which minimal bandwidth could be realized by coincidence filters.

On the initiation by Tischner the properties of coincidence filters operated by rectangular impulses have been investigated by Schie f and by Kosel. Rectangular impulses have the advantage, that moderate variations of the amplitudes do not disturb the coincidence. In this case however very small impulse durations are required for the realization of small bandwidth.

In the present paper the operation of coincidence filters by non rectangular impulses has been considered. Having the shape of an excitatory post-synaptic potential of motoneurons, the impulses are completely determined by the rising phase and the falling phase. These impulses have been termed short impulses in contrast to the rectangular impulses, which are long, compared to the duration of their rising and falling phases. The width of the short impulses decreases with increasing measuring level. Close to the amplitude the width becomes very small, which theoretically provides a very small functional bandwidth. The practical realization of very small functional bandwidth is heavily limited by the big variations which will be caused by minute alterations of the amplitudes as introduced by noise. The variation of the functional bandwidth caused by 1% alteration of the amplitude has been termed the error factor. In the present paper some relationships between the following four quantities have been worked out: realizable functional bandwidth, tolerable variation of functional bandwidth, error factor, and given variation of the amplitudes and thresholds (noise).

The short impulses have been piecewise approximated by analytical functions (parabolic and hyperbolic) which in general permits an analytical treatment of the problems.