Abstract
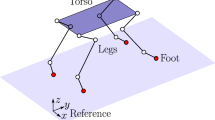
A unified dynamic modelling approach of closed and/or open kinematic chain mechanisms is established. It is based on the use of the Newton-Euler formalism and the explicit formulation of kinematic holonomic constraints for the closed loop mechanisms. The approach is then applied to derive the dynamic modelling of a four-legged robot adopting a walking gait. The different movement sequences of the gait are analysed in order to calculate the all necessary terms in the dynamic equations of the quadruped robot.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Abbreviations
- g :
-
acceleration vector due to the gravity
- m i :
-
mass of bodyS i
- G i :
-
mass centre of bodyS i
- I i :
-
inertia tensor of the bodyS i about its mass centre
- f :
-
coefficient of viscous friction
- V Gi :
-
3-dim absolute velocity vector
- Ωi :
-
3-dim absolute angular velocity vector
- t i :
-
6-dim twist vector of the bodyS i defined as\(t_i = \left[ {V_{G_i }^T ,\Omega _i^T } \right]^T \)
- n, l :
-
number of bodies, joints
- d i :
-
number of degree of freedom of the jointi
- I d :
-
3×3 identity matrix
- T suprinfi :
-
6-dim wrench vector acting on the bodyS i in whichr stands for:l (constraint wrench),g (gravity wrench),f (friction wrench),e (external wrench),m (driving wrench)
- θi :
-
joint angle of the bodyS i
- O(3) :
-
3-dim zero vector
References
Wittenburg, J.:Dynamics of Systems of Rigid Bodies, B. G. Tenbrer, Stuttgart, 1977.
Furusho, J. and Sano, A.: Sensor based control of a nine-link biped,Internat. J. Robotics Res. 9(2) (1990), 83–98.
Gorinevsky, D. M. and Shneider, Yu. A.: Force control in locomotion of legged vehicles over rigid and soft surfaces,Internat. J. Robotics Res. 9(2) (1990), 4–23.
Kleinfenger, J. F.: Modélisation dynamique de robots à chaîne cinématique simple, arborescente ou fermée en vue de leur commande, Doctoral Thesis, Nantes, France.
Mybridge, E.:Animals in Motion, Dover Publications, New York, 1957.
Bennani, M. and Giri, F.: Kinematic modelling of a four-legged robot,ASME J. Mechanics, Transmission and Automation in Design, 1996, in press.
Jerkovsky, W.: The structure of multibody dynamical equations,J. Guidance and Control 1(3) (1978), 173–182.
Angeles, J. and Lee, S.: Dynamic modelling of holonomic mechanical system using a natural orthogonal complement matrix, Part I: Formulation,Proc. 9th Symp. Engineering Applications of Mechanics, London, Ont., May 29–31, 1988.
Earl, C. F. and Rooney, J.: Some kinematic structures for robot manipulator designs,ASME J. Mechanics, Transmission and Automation in Design,105(1) (19??), 15–22.
Sun, S. S.: A theoretical study of gaits for legged locomotion system, Ph.D. Dissertation, The Ohio State University, Columbus, OH, March 1974.
Hirose, S.: A study of design and control of a quadrupled walking vehicle,Internat. J. Robotics Res. 3(2) (1984), 113–133.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Bennani, M., Giri, F. Dynamic modelling of a four-legged robot. J Intell Robot Syst 17, 419–428 (1996). https://doi.org/10.1007/BF00571701
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00571701