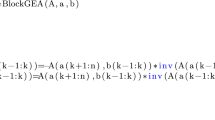Skip to main content

Advertisement

Springer Nature Link
Log in

2-D FFT algorithm by matrix factorization in a 2-D space

  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

Abstract

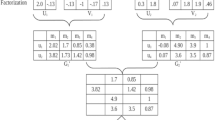
A new 2-D FFT algorithm is described. This algorithm applies a 2-D matrix factorization technique in a 2-D space and offers a way to do 2-D FFT in both dimensions simultaneously. The computation is greatly reduced compared to traditional algorithms. This will improve the realization of a 2-D FFT on any kind of computer. However its good parallelism will especially benefit an implementation on a computer with hypercube architecture. A good arrangement of parallel processors will save a great deal of running time. Furthermore this algorithm can be extended toM-D cases forM>2.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. F. Theilheimer, “A Matrix Version of the Fast Fourier Transform,”IEEE Trans., vol. AU-17, no. 2, 1969, pp. 158–161.

    Google Scholar 

  2. D.K. Kahaner, “Matrix Description of the Fast Fourier Transform,”IEEE, vol. AU-18, no. 4, December 1970, pp. 442–450.

    Google Scholar 

  3. E.O. Brigham, “The Fast Fourier Transform,” Englewood Cliffs, NJ: Prentice-Hall, 1974.

    Google Scholar 

  4. H.C. Andrews, and W.K. Pratt, “Digital Computer Simulation of Coherent Optical Processing Operations,”Computer Group News, November 1968, pp. 12–19.

  5. M. Jagadeesan, “N-Dimensional Fast Fourier Transform,”13th Midwest Symp. Circuit Theory, Minneapolis, MN, May, 1970, pp. 3.2.1–3.2.8.

  6. H.J. Nussbaumer, “New Algorithms for Convolution and DFT Based on Polynomial Transforms,”1978 Proc. IEEE Int. Conf. ASSP, 1978, pp. 638–641.

  7. H.J. Nussbaumer, and P. Quandalle, “Fast Computation of Discrete Fourier Transforms Using Polynomial Transforms,”IEEE, vol. ASSP-27, no. 2, 1979, pp. 169–181.

    Google Scholar 

  8. D.B. Harris, J.H. McClellan, D.S.K. Chan, and H.W. Schuessler, “Vector Radix Fast Fourier Transform,”1977 IEEE Int. Conf. ASSP Record, pp. 548–551.

  9. A. Guessoum, and R.M. Merserean, “Fast Algorithms for the Multidimensional Discrete Fourier Transform,”IEEE, vol. ASSP-34, no. 4, August 1986, pp. 937–943.

    Google Scholar 

  10. W.M. Gentleman, and G. Sande, “The Fast Fourier Transform for Fun and Profit,”AFIPS Proc., 1966 Fall Joint Computer Conf. vol. 29, Washington, D.C., pp. 563–678.

  11. A. Granham, “Kronecker Products and Matrix Calculus with Applications,” New York: Ellis Horwood 1981.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Control Science and Dynamical Systems Center, University of Minnesota, 55455, Minneapolis, MN

    M. Wang & E. B. Lee

Authors
  1. M. Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. E. B. Lee
    View author publications

    You can also search for this author inPubMed Google Scholar

Additional information

Supported by NSF Grant CCR-8813493.

Supported by Grants DMS-8607687, DMS-8722402, and DMS9002019.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, M., Lee, E.B. 2-D FFT algorithm by matrix factorization in a 2-D space. Multidim Syst Sign Process 5, 61–74 (1994). https://doi.org/10.1007/BF00985863

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00985863

Key Words